Équations de Stokes

Équations de Stokes: Écoulement de Stokes

Pour les articles homonymes, voir Stokes.

Lorsqu'un fluide visqueux s'écoule lentement en un lieu étroit ou autour d'un petit objet, les effets visqueux dominent sur les effets inertiels. Son écoulement est alors appelé écoulement de Stokes (et on parle parfois de fluide de Stokes par opposition à fluide parfait). Il est en effet régi par une version simplifiée de l'équation de Navier-Stokes : l' équation de Stokes, dans laquelle les termes inertiels sont absents. Le nombre de Reynolds mesure le poids relatif des termes visqueux et inertiel dans l'équation de Navier-Stokes. L'écoulement de Stokes correspond ainsi à un faible nombre de Reynolds (beaucoup plus petit que 1).

L'équation de Stokes permet en particulier de décrire les écoulements de liquide dans les dispositifs microfluidiques. Les écoulements de Couette et de Poiseuille sont aussi décrits par cette équation.

Sommaire

1 Équation de Stokes

2 Conditions d'application

3 Propriétés des solutions de l'équation de Stokes

4 Références

5 Bibliographie

6 Articles connexes

Équation de Stokes

L'équation de Stokes, qui décrit l'écoulement d'un fluide newtonien incompressible en régime permanent et à faible nombre de Reynolds, s'écrit :

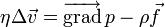$\eta \Delta \vec{v} = \overrightarrow{\mathrm{grad}}\,p - \rho \vec{f}$ ,

où :

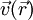$\vec{v} (\vec{r})$ est la vitesse du fluide ;

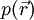$p (\vec{r})$ est la pression dans le fluide ;

$ρ$ est la masse volumique du fluide

$η$ est la viscosité dynamique du fluide;

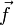$\vec{f}$ est une force massique s'exerçant dans le fluide (par exemple : pesanteur) ;

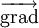$\overrightarrow{\mathrm{grad}}$ et $Δ$ sont respectivement les opérateurs différentiels gradient et laplacien.

Conditions d'application

L'équation de Stokes est une forme simplifiée de l'équation de Navier-Stokes. Pour un fluide newtonien, celle-ci s'écrit :

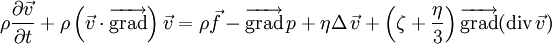$\rho \frac{ \partial \vec{v} }{ \partial t } + \rho \left(\vec{v} \cdot \overrightarrow{\mathrm{grad}}\right)\vec{v} = \rho \vec{f} - \overrightarrow{\mathrm{grad}}\,p + \eta \Delta\,\vec{v} + \left( \zeta + \frac{\eta}{3} \right) \overrightarrow{\mathrm{grad}} (\mathrm{div}\,\vec{v})$ ,

où :

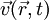$\vec{v} (\vec{r},t)$ est la vitesse du fluide ;

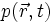$p (\vec{r},t)$ est la pression dans le fluide ;

$ρ$ est la masse volumique du fluide

$η$ est la viscosité dynamique en cisaillement du fluide;

$ζ$ est la viscosité dynamique en compression du fluide;

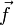$\vec{f}$ est une force massique s'exerçant dans le fluide (par exemple : pesanteur) ;

$t$ représente le temps ;

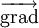$\overrightarrow{\mathrm{grad}}$ , $div$ et $Δ$ sont respectivement les opérateurs différentiels gradient, divergence et laplacien.

NB : pour établir cette formule, on doit supposer que les variations spatiales de $η$ et $ζ$ sont négligeables.

Si de plus le fluide est incompressible (bonne approximation pour les liquides), alors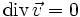 $\text{div}\,\vec{v} = 0$ et l'équation se simplifie :

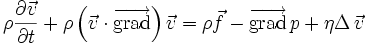$\rho \frac{ \partial \vec{v} }{ \partial t } + \rho \left(\vec{v} \cdot \overrightarrow{\mathrm{grad}}\right)\vec{v} = \rho \vec{f} - \overrightarrow{\mathrm{grad}}\,p + \eta \Delta\,\vec{v}$ .

On peut évaluer l'ordre de grandeur des termes inertiels et visqueux dans cette équation. Si la vitesse caractéristique du liquide est $U$ , et si l'échelle typique de variation de la vitesse est $L$ (celle-ci pourra être imposée par les dimensions du canal dans lequel le liquide s'écoule, les dimensions de l'objet autour duquel le liquide s'écoule, etc.), alors :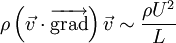

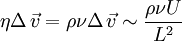$\rho \left(\vec{v} \cdot \overrightarrow{\mathrm{grad}}\right)\vec{v} \sim \frac{\rho U^2}{L}$ et $\eta \Delta\,\vec{v} = \rho \nu \Delta\,\vec{v} \sim \frac{\rho \nu U}{L^2}$ ,

où $ν$ est la viscosité cinématique du liquide.

Le terme inertiel 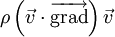$\rho \left(\vec{v} \cdot \overrightarrow{\mathrm{grad}}\right)\vec{v}$ sera donc négligeable devant le terme visqueux 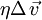$\eta \Delta\,\vec{v}$ si :

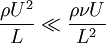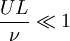$\frac{\rho U^2}{L} \ll \frac{\rho \nu U}{L^2}$ , soit $\frac{UL}{\nu} \ll 1$ ,

où l'on reconnait l'expression du nombre de Reynolds.

Propriétés des solutions de l'équation de Stokes

Contrairement à l'équation de Navier-Stokes, l'équation de Stokes est linéaire (le terme inertiel, non-linéaire, est en effet négligeable). Les écoulements solutions de cette équation possèdent par conséquent des propriétés bien particulières :

unicité : pour des conditions aux limites données (valeur de la vitesse au niveau des parois et/ou à l'infini), il existe un et un seul écoulement vérifiant l'équation de Stokes ;

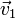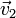additivité : les solutions de l'équation de Stokes vérifient le principe de superposition : si $\vec{v}_1$ et $\vec{v}_2$ sont solutions, alors toute combinaison linéaire 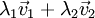$\lambda_1 \vec{v}_1 + \lambda_2 \vec{v}_2$ le sera aussi (ceci n'est pas incompatible avec la propriété d'unicité : seul l'écoulement vérifiant les bonnes conditions aux limites sera observé) ;

réversibilité : si un champ de vitesse 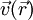$\vec{v}(\vec{r})$ est solution de l'équation, alors 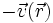$- \vec{v}(\vec{r})$ l'est aussi, à condition de changer le signe des gradients de pression, ainsi que des vitesses aux parois et à l'infini (ceci est une conséquence directe du principe de superposition) ; cette propriété est contraire à notre intuition, fondée sur notre expérience des écoulements macroscopiques : la réversibilité des écoulements à bas nombre de Reynolds a ainsi poussé les êtres vivants de très petite taille à développer des moyens de propulsion originaux ^[1].

paradoxe de Stokes : Il faut prendre garde au fait que les solutions mathématiques de l'équation de Stokes, dans un cas donné ou dans certaines régions du domaine de solution, peuvent être physiquement fausses. Ceci est dû au "paradoxe de Stokes" à savoir que les conditions physiques permettant de ramener l'équation de N-S à l'équation de Stokes ne sont pas nécessairement réalisées dans tout le domaine de solution, a priori. On aboutit alors à des solutions présentant des comportements potentiellement aberrants dans certaines limites. C'est le cas par exemple "à l'infini" où souvent le terme inertiel finit par l'emporter sur le terme visqueux, sans qu'on puisse le préjuger a priori.

Références

↑ E.M. Purcell, «Life at low Reynolds number», Am. J. Phys. 45, p. 3-11.

Bibliographie

(en) G.K. Batchelor, An Introduction to Fluid Dynamics [« Introduction à la dynamique des fluides »], Cambridge University Press, 1967.

E. Guyon, J.-P. Hulin, L. Petit, Hydrodynamique physique, CNRS Editions - EDP Sciences, 2^e éd. (1^re éd. 1991), 2001.

J. Happel et H. Brenner, Low Reynolds number hydrodynamics [«Hydrodynamique à bas nombre de Reynolds»], Prentice Hall, 1965.

Articles connexes

Écoulement laminaire

Nombre de Reynolds

Turbulence

Portail de la physique

Ce document provient de « %C3%89coulement de Stokes ».

Catégorie : Équations de Navier-Stokes

Contenu soumis à la licence CC-BY-SA. Source : Article Équations de Stokes de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Stokes — may refer to:People: See Stokes (surname) cience* Stokes (unit), a measure of viscosity *Stokes flow *Stokes law *Stokes law (sound attenuation) *Stokes parameters *Stokes radius *Stokes relations *Stokes shift *Stokes theorem *Navier Stokes… … Wikipedia
Stokes equation — may refer to:* the Airy equation * the equations of Stokes flow, a linearised form of the Navier–Stokes equations in the limit of small Reynolds number … Wikipedia
Equations de Navier-Stokes — Équations de Navier Stokes Pour les articles homonymes, voir Stokes. En mécanique des fluides, les équations de Navier Stokes sont des équations aux dérivées partielles non linéaires qui décrivent le mouvement des fluides dans l approximation des … Wikipédia en Français
Équations de navier-stokes — Pour les articles homonymes, voir Stokes. En mécanique des fluides, les équations de Navier Stokes sont des équations aux dérivées partielles non linéaires qui décrivent le mouvement des fluides dans l approximation des milieux continus. Elles… … Wikipédia en Français
Stokes boundary layer — in a viscous fluid due to the harmonic oscillation of a plane rigid plate. Velocity (blue line) and particle excursion (red dots) as a function of the distance to the wall. In fluid dynamics, the Stokes boundary layer, or oscillatory boundary… … Wikipedia
Equations primitives atmospheriques — Équations primitives atmosphériques Les équations primitives atmosphériques sont une version simplifiée des équations de Navier Stokes. Elles sont applicables dans le cas d’un fluide à la surface d’une sphère en posant comme hypothèses que la… … Wikipédia en Français
Equations de Yang-Mills — Équations de Yang Mills Une théorie de Yang Mills est un type de théorie de jauge non abélienne, dont le premier exemple a été introduit dans les années 1950 par les physiciens Chen Ning Yang, et Robert Mills pour obtenir une description… … Wikipédia en Français
Équations de Yang-Mills — Une théorie de Yang Mills est un type de théorie de jauge non abélienne, dont le premier exemple a été introduit dans les années 1950 par les physiciens Chen Ning Yang, et Robert Mills pour obtenir une description cohérente de l interaction… … Wikipédia en Français
Équations de yang-mills — Une théorie de Yang Mills est un type de théorie de jauge non abélienne, dont le premier exemple a été introduit dans les années 1950 par les physiciens Chen Ning Yang, et Robert Mills pour obtenir une description cohérente de l interaction… … Wikipédia en Français
Stokes (unite) — Stokes (unité) Pour les articles homonymes, voir Stokes. Le stokes (symbole St) est l unité CGS de viscosité cinématique. Il vaut 1 St = 1 cm²/s = 10 4 m²/s. Il est ainsi nommé en l honneur du physicien irlandais George Stokes. Dans un écoulement … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Équations de Stokes

Écoulement de Stokes

Sommaire

Équation de Stokes

Conditions d'application

Propriétés des solutions de l'équation de Stokes

Références

Bibliographie

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Équations de Stokes

Écoulement de Stokes

Sommaire

Équation de Stokes

Conditions d'application

Propriétés des solutions de l'équation de Stokes

Références

Bibliographie

Articles connexes

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link