Théorème de frobenius généralisé

Théorème de frobenius généralisé: Théorème de Frobenius généralisé

Le théorème de Frobenius généralisé est un théorème d'algèbre générale qui étend le théorème de Frobenius de 1877.

En 1843, Hamilton a souhaité étendre les propriétés d'algèbre normée des nombres complexes en considérant des triplets de réels. Il ne put effectuer cette généralisation qu'en considérant des quadruplets de réels, et en abandonnant la commutativité du produit, il obtint les quaternions.

En 1845, Cayley poursuit l'extension de la construction à huit dimensions, en abandonnant également l'associativité du produit, compensée par les lois alternatives $x (x y) = x 2 y$ et $(y x) x = y x 2$ .

En 1877, Frobenius a montré un théorème qui donne une classification des algèbres de division associatives de dimension finie sur le corps des réels (il s'agit de $\R$ (réels), 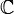$\Complex$ (complexes) et 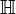$\mathbb{H}$ (quaternions)).

Nous donnons ici une généralisation de ce théorème :

Théorème de Frobenius généralisé — Les seules algèbres de division alternatives de dimension finie sur le corps des réels sont $\R$ (réels), 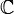$\Complex$ (complexes), 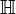$\mathbb{H}$ (quaternions) et $\mathbb{O}$ (octonions).

Sommaire

1 Lemmes préliminaires

2 Démonstration

2.1 Point 1

2.2 Point 2

3 Notes et références

4 Voir aussi

4.1 Articles connexes

Lemmes préliminaires

Il est utile d'utiliser l'associateur $A$ de $x, y, z$ . Soit une algèbre alternative (qui satisfait les lois alternatives qui se traduisent par $A (x, x, y) = A (y, x, x) = 0$ ) sur un corps 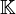$\mathbb{K}$ et $x, y, z$ trois éléments de cette algèbre.

Lemme 1 — L'associateur est alterné :
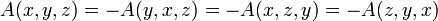$A(x,y,z)=-A(y,x,z)=-A(x,z,y)=-A(z,y,x)\,$ .

En effet, par la première loi alternative on a
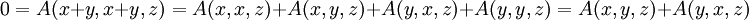
$0=A(x+y,x+y,z)=A(x,x,z)+A(x,y,z)+A(y,x,z)+A(y,y,z)=A(x,y,z)+A(y,x,z) \,$

Lemme 2 — La loi flexible $x (y x) = (x y) x$ est valide.

En effet, par le lemme 1, $A (x, y, x) = - A (y, x, x)$ .

Lemme 3 — Si $x$ et $y$ anticommutent ( $x y = - y x$ ), alors $x (y z) = - y (x z)$ et $(z x) y = - (z y) x$ .

En effet, par le lemme 1, $A (x, y, z) + A (y, x, z) = 0$ , et si $x y + y x = 0$ , alors $0 = A (x, y, z) + A (y, x, z) + (x y + y x) z = x (y z) + y (x z)$ , soit $x (y z) = - y (x z)$ . L'autre égalité se démontre de même.

Lemme 4 — L'identité de Moufang $(z x)(y z) = (z (x y)) z$ est valide (on dit que le produit est neutroactif).

En effet,
$\begin{align} (zx)(yz)-((zx)y)z & = A(zx,y,z) = A(y,z,zx)=y(z^2x)-(yz)(zx)\\ & = y(z^2x)-A(yz,z,x)-(yz^2)x=A(y,z^2,x)-A(yz,z,x) \\ & = A(y,z^2,x)-1(x,yz,z)=A(y,z^2,x)-x(yz^2)+(x(yz))z \\ & = A(y,z^2,x)+A(x,y,z)z-A(x,y,z^2)=A(x,y,z)z \end{align}$
D'où $(z x)(y z) = A (x, y, z) z + ((z x) x) z = A (x, y, z) z - A (z, x, y) z + (z (x y)) z = (z (x y)) z$ .

Lemme 5 — En définissant par récurrence $x 1 = x$ puis $x n + 1 = x n x$ pour 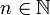$n \in \N$ , on a $x n x m = x n + m$ .

Par récurrence sur $m$ , avec la loi flexible on obtient $x x m = x m + 1$ .

Puis par récurrence sur $n$ , comme la propriété est vraie par définition pour $m = 1$ , alors on peut supposer $m > 1$ et l'hérédité vient de l'identité de Moufang :
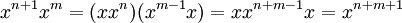$x^{n+1}x^m=(xx^n)(x^{m-1}x)=xx^{n+m-1}x=x^{n+m+1} \,$ .
Démonstration

Soit $D$ une algèbre de division alternative de dimension finie sur le corps des réels.

Point 1

Si 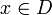$x \in D$ , alors $x^2 \in \R + \R x$ .

Par le lemme 5, l'application
$\begin{matrix}\R[X]&\rightarrow&D\\X&\mapsto&x\end{matrix}$
est un morphisme d'algèbre.

La famille ${1, x, x 2,...}$ des puissances d'un élément 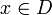$x\in D$ est liée. En effet, si cette famille est finie, il y a un relation du type $x n = x m$ avec $n\neq m$ et si elle est infinie, cela vient de la dimension finie de $D$ .

Etant donné qu'un polynôme à coefficients réels est produit de polynômes de degré un ou deux (cf. Factorisation des polynômes), et comme $D$ n'admet pas de diviseur de zéro, on en déduit que $x$ vérifie une équation du second degré à coefficients réels, soit $x^2 \in \R + \R x$ .

Point 2

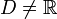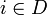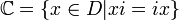Si $D\neq\R$ , alors il existe $i\in D$ tel que $i 2 = - 1$ . $\Complex =\R+\R i$ est un corps isomorphe à celui des nombres complexes et $\Complex=\{x\in D |xi=ix\}$ .

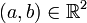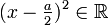En effet, par le point 1, $x 2 = a x + b$ avec $(a,b)\in\R^2$ , d'où $(x-\tfrac{a}{2})^2\in\R$ .

Ainsi, si 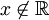$x\not\in\R$ , il faut que 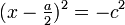$(x-\tfrac{a}{2})^2=-c^2$ avec $c\in\R$ .

On en déduit que si 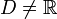$D\neq\R$ , alors d'une part il existe 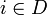$i\in D$ tel que $i 2 = - 1$ , et d'autre part si 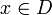$x\in D$ et $x i = i x$ alors 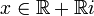$x\in \R+\R i$ (en effet si 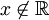$x\not\in\R$ , alors 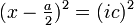$(x-\tfrac{a}{2})^2=(ic)^2$ , et avec $x i = i x$ on a
$\left(x-\frac{a}{2}\right)^2-(ic)^2=\left(x-\frac{a}{2}+ic\right)\left(x-\frac{a}{2}-ic\right )=0$
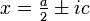soit $x=\tfrac{a}{2}\pm ic$ ).

Notes et références

(en) Angel Oneto, Alternative Real Division Algebras of Finite Dimension

Voir aussi

Articles connexes

Théorème de Frobenius

Octonion

Associativité

Alternativité

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Frobenius g%C3%A9n%C3%A9ralis%C3%A9 ».

Catégorie : Algèbre générale

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de frobenius généralisé de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Theoreme de Frobenius generalise — Théorème de Frobenius généralisé Le théorème de Frobenius généralisé est un théorème d algèbre générale qui étend le théorème de Frobenius de 1877. En 1843, Hamilton a souhaité étendre les propriétés d algèbre normée des nombres complexes en… … Wikipédia en Français
Théorème de Frobenius généralisé — Pour les articles homonymes, voir Théorème de Hurwitz. Le théorème de Frobenius généralisé (connu également sous le nom de théorème de Hurwitz[1], bien que ce dernier en soit une forme plus générale encore) est un théorème d algèbre générale qui… … Wikipédia en Français
Theoreme de densite de Chebotarev — Théorème de densité de Chebotarev Le théorème de Chebotarev généralise, en quelque sorte, le théorème de Dirichlet sur l infinitude des nombres premiers en progressions arithmétiques. Ce dernier stipule que, si sont deux entiers premiers entre… … Wikipédia en Français
Théorème de densité de chebotarev — Le théorème de Chebotarev généralise, en quelque sorte, le théorème de Dirichlet sur l infinitude des nombres premiers en progressions arithmétiques. Ce dernier stipule que, si sont deux entiers premiers entre eux, la densité naturelle de l… … Wikipédia en Français
Théorème de densité de Chebotarev — En théorie algébrique des nombres, le théorème de Chebotarev généralise, en quelque sorte, le théorème de la progression arithmétique de Dirichlet sur l infinitude des nombres premiers en progression arithmétique. Ce dernier stipule que, si sont… … Wikipédia en Français
Theoreme de Burnside (groupe resoluble) — Théorème de Burnside (groupe résoluble) William Burnside En mathématiques, et plus précisément dans le contexte de la théorie des groupes finis, le théorème de Burnside traite des groupes résolubles. Ce théorème stipule que, si p et q sont deux… … Wikipédia en Français
Théorème de burnside (groupe résoluble) — William Burnside En mathématiques, et plus précisément dans le contexte de la théorie des groupes finis, le théorème de Burnside traite des groupes résolubles. Ce théorème stipule que, si p et q sont deux nombres premiers et n et m deux … Wikipédia en Français
Ferdinand Georg Frobenius — Pour les articles homonymes, voir Frobenius. Ferdinand Georg Frobenius. Ferdinand Georg Frobenius, connu aussi sous le nom de Georg Frobenius, né le 26 octobre& … Wikipédia en Français
Georg Ferdinand Frobenius — Ferdinand Georg Frobenius Pour les articles homonymes, voir Frobenius. Ferdinand Georg Frobenius. Ferdinand Georg Frobenius, connu aussi sous le nom de Georg Froben … Wikipédia en Français
Georg Frobenius — Ferdinand Georg Frobenius Pour les articles homonymes, voir Frobenius. Ferdinand Georg Frobenius. Ferdinand Georg Frobenius, connu aussi sous le nom de Georg Froben … Wikipédia en Français

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts