- Théorème de fubini
-
Théorème de Fubini
En mathématiques, le théorème de Fubini fournit des informations sur le calcul d'intégrales définies sur des ensembles produits et permet le calcul de telles intégrales. Il indique que sous certaines conditions, pour intégrer une fonction à plusieurs variables, on peut intégrer les variables les unes à la suite des autres.
Sommaire
Énoncés
Théorème de Fubini-Tonelli — Soient
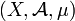 et
et 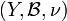 deux espaces mesurés tels que les deux mesures soient σ-finies. Si
deux espaces mesurés tels que les deux mesures soient σ-finies. Si 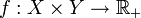 est mesurable pour
est mesurable pour 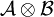 (voir tribu produit) et positive sur
(voir tribu produit) et positive sur 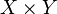 , alors les applications
, alors les applications 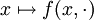 et
et 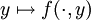 ainsi que les applications
ainsi que les applicationssont mesurables positives. On a de plus
où on a noté ζ la mesure produit sur
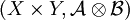 .
.Théorème de Fubini-Lebesgue — Soient
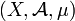 et
et 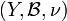 deux espaces mesurés tels que les deux mesures soient σ-finies. Si
deux espaces mesurés tels que les deux mesures soient σ-finies. Si 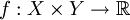 est intégrable sur
est intégrable sur 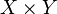 pour
pour 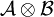 (voir tribu produit), alors la fonction
(voir tribu produit), alors la fonction 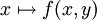 est intégrable pour presque tout
est intégrable pour presque tout 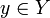 , la fonction
, la fonction 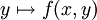 est intégrable pour presque tout
est intégrable pour presque tout 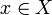 . En outre, les fonctions
. En outre, les fonctionssont intégrables. On a de plus
où on a noté ζ la mesure produit sur
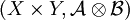 .
.Une mesure μ sur un espace X est dite σ-finie si et seulement s'il existe une réunion dénombrable de sous-ensembles de X de mesure finie et tel que la réunion est égale à X. C'est le cas de la mesure de Lebesgue. Les deux théorèmes sont faux si on ne suppose pas les mesures σ-finies.
Mise en œuvre
L'utilisation combinée de ces deux théorèmes permet souvent de démontrer qu'une fonction mesurable est intégrable. En effet, pour
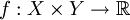 mesurable, on peut appliquer le théorème de Fubini-Tonelli à | f | , ce qui donne
mesurable, on peut appliquer le théorème de Fubini-Tonelli à | f | , ce qui donneLe calcul des intégrales étant maintenant souvent plus aisée, si l'une des intégrales est finie, alors ceci montre que f est intégrable, et on a de plus d'après le théorème de Fubini-Lebesgue
ce qui permet le calcul de l'intégrale.
Applications
- Dans le cas où
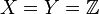 et où les mesures sur X et Y sont les mesures de dénombrement, on obtient le théorème suivant sur les séries doubles.
et où les mesures sur X et Y sont les mesures de dénombrement, on obtient le théorème suivant sur les séries doubles.
Permutation d'une série double — Si
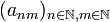 est une famille de réels positifs ou nuls, ou une famille de complexes telle que
est une famille de réels positifs ou nuls, ou une famille de complexes telle que 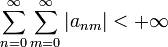 , alors
, alors 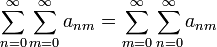
- Le produit de convolution de deux fonctions intégrables est lui-même intégrable.
- Calcul de l'intégrale de Gauss
∫ exp( − x2)dx R .
Contre-exemples
Si f n'est pas intégrable
Considérons
On a en intégrant tout d'abord par rapport à y:
Puis
On a donc
De manière symétrique, on a
Le théorème de Fubini ne s'applique par ici. En effet, la fonction considérée ici n'est pas intégrable :
Cas d'une mesure non sigma-finie
Considérons l'ensemble I = [0,1]. Munissons le d'une part de la tribu borélienne
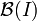 et de la mesure de Lebesgue λ et d'autre part de la tribu constituée de l'ensemble
et de la mesure de Lebesgue λ et d'autre part de la tribu constituée de l'ensemble 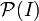 des parties de I muni de la mesure de dénombrement.
des parties de I muni de la mesure de dénombrement.Posons
![\Delta=\{(x,x)\ /\ x \in [0,1]\}](/pictures/frwiki/101/ec401454af1da225a47bbfed180941c6.png) . Comme
. Comme 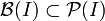 , on a
, on a 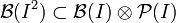 . De plus,
. De plus, 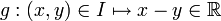 est continue, donc Δ = g − 1({0}) est fermé dans I. On en déduit que
est continue, donc Δ = g − 1({0}) est fermé dans I. On en déduit que 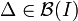 . Par suite,
. Par suite, 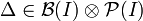 . La fonction indicatrice 1Δ est donc mesurable sur l'espace produit considéré.
. La fonction indicatrice 1Δ est donc mesurable sur l'espace produit considéré.D'un part, considérons
Pour x fixé, on a 1Δ(x,y) qui vaut 0 si
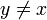 , 1 si x = y. On a donc 1Δ(x,y) = 1{x}(y). D'où
, 1 si x = y. On a donc 1Δ(x,y) = 1{x}(y). D'oùA1 = ∫ m({x})dλ(x) = ∫ dλ(y) = 1. I I D'autre part, on a
La théorème de Fubini ne s'applique pas ici (car sinon 0=1). Ceci s'explique car la mesure de dénombrement n'est pas σ-finie sur [0,1]. En effet, si elle l'était, cela signifie que [0,1] s'écrirait comme une réunion dénombrable d'ensembles de mesure finie, c'est-à-dire d'ensembles finis. L'intervalle [0,1] serait donc dénombrable, ce qui est absurde.
Voir aussi
Liens internes
Liens externes
- [1] Un polycopié de cours de M. Mazet sur les mesures produits. On y trouve une preuve des deux versions du théorème de Fubini.
Bibliographie
Walter Rudin, Analyse réelle et complexe : cours et exercices [détail des éditions]
- Portail des mathématiques
Catégories : Théorie de la mesure | Théorème de mathématiques
Wikimedia Foundation. 2010.

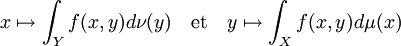
![\iint_{X \times Y} f(x,y) d\zeta(x,y) = \int_X \left[ \int_Y f(x,y) d\nu(y) \right] d\mu(x) = \int_Y \left[ \int_X f(x,y) \,d\mu(x) \right] d\nu(y)](/pictures/frwiki/98/bc9d14ce2444ea71ad5371f218909f81.png)
![\iint_{X \times Y} |f(x,y)| d\zeta(x,y) = \int_X \left[ \int_Y |f(x,y)| d\nu(y) \right] d\mu(x) = \int_Y \left[ \int_X |f(x,y)|\,d\mu(x) \right] d\nu(y)](/pictures/frwiki/57/998cf920088cad8e5eb689a44d018232.png)
![\int_{[0,1]^2} \frac{x^2-y^2}{(x^2+y^2)^2} d(x,y).](/pictures/frwiki/53/527e17e48238b1f92539f49f28987fee.png)
![\begin{align} \int_0^1\frac{x^2-y^2}{(x^2+y^2)^2}\,dy & = \int_0^1 \frac{x^2 + y^2 - 2y^2}{(x^2 + y^2)^2} \, dy\\
&= \int_0^1 \frac{1}{x^2 + y^2} \, dy + \int_0^1 \frac{-2y^2}{(x^2 + y^2)^2} \, dy\\
&= \int_0^1 \frac{1}{x^2 + y^2} \, dy + \int_0^1 y \left(\frac{d}{dy} \frac{1}{x^2 + y^2}\right) \, dy\\
&= \int_0^1 \frac{1}{x^2 + y^2} \, dy + \left(\left[\frac{y}{x^2 + y^2}\right]_{y=0}^1 - \int_0^1 \frac{1}{x^2 + y^2} \, dy\right)\\
&= \frac{1}{1 + x^2}.\end{align}](/pictures/frwiki/101/ec6748170a17ae982fd7944ee7560627.png)
![\int_0^1\frac{1}{1+x^2}\,dx=\left[\arctan(x)\right]_0^1=\arctan(1)-\arctan(0)=\frac{\pi}{4}.](/pictures/frwiki/53/59b4e4a0a3a90c576f2bc88aee7f682f.png)
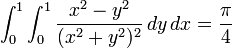
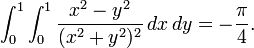
![\int_0^1\int_0^1
\left|\frac{x^2-y^2}{(x^2+y^2)^2}\right|\,dx\,dy=\int_0^1\left[\int_0^y
\frac{y^2-x^2}{(x^2+y^2)^2}\,dx+\int_y^1\frac{x^2-y^2}{(x^2+y^2)^2}\,dx\right]\,dy](/pictures/frwiki/97/a5a7f29de9fc26b77618c7cb0a5452cb.png)
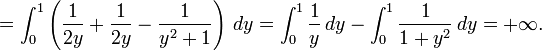
![A_1=\int_I \left[ \int_I 1_\Delta(x,y) dm(y) \right] d\lambda(x).](/pictures/frwiki/57/92cbff1348f93f81a6a0e88ababea8f9.png)
![A_2=\int_I \left[ \int_I 1_\Delta(x,y) d\lambda(x) \right] dm(y)=\int_I \lambda(\{x\}) dm(y)=\int_I0dm(y)=0.](/pictures/frwiki/102/f95e73282e031258580b6315cad10226.png)