Theoreme de densite de Chebotarev

Theoreme de densite de Chebotarev

Théorème de densité de Chebotarev

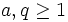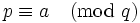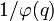Le théorème de Chebotarev généralise, en quelque sorte, le théorème de Dirichlet sur l'infinitude des nombres premiers en progressions arithmétiques. Ce dernier stipule que, si a,q \geq 1 sont deux entiers premiers entre eux, la densité naturelle de l'ensemble des nombres premiers p \equiv a \pmod q vaut 1/\varphi(q).

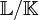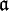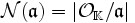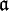Le cadre du théorème de Chebotarev est le suivant : on considère une extension galoisienne \mathbb {L} / \mathbb {K} de corps de nombres, de groupe de Galois G. Pour tout idéal entier \mathfrak {a} de \mathbb {K}, on note \mathcal {N}(\mathfrak {a}) = \left | \mathcal {O}_{\mathbb {K}} / \mathfrak {a}\right | la norme de \mathfrak {a}.

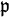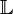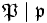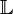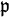Considérons un idéal premier \mathfrak {p} de \mathbb {K} non ramifié dans \mathbb {L}, et soit \mathfrak {P} \mid \mathfrak {p} un idéal premier de \mathbb {L} au-dessus de \mathfrak {p}.

On montre qu'il existe un unique élément 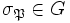\sigma_{\mathfrak {P}} \in G caractérisé par la relation suivante : pour tout élément 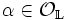\alpha \in \mathcal {O}_{\mathbb {L}}, on a

\sigma_{\mathfrak {P}} (\alpha) \equiv \alpha^{\mathcal {N}(\mathfrak {p})} \pmod {\mathfrak {P}}.

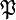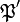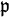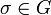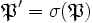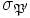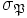Si G n'est pas abélien, cela dépend du choix de \mathfrak {P} : en effet, si \mathfrak {P'} est un autre idéal premier au-dessus de \mathfrak {p}, il existe un élément \sigma \in G tel que \mathfrak {P'} = \sigma ( \mathfrak {P}), et alors \sigma_{\mathfrak {P'}} et \sigma_{\mathfrak {P}} sont conjugués dans G.

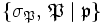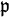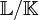On considère alors la classe de conjugaison \{ \sigma_{\mathfrak {P}}, \, \mathfrak {P} \mid \mathfrak {p} \}, que l'on nomme symbole de Frobénius de \mathfrak {p} dans \mathbb {L} / \mathbb {K}, encore noté (par abus) 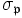\sigma_{\mathfrak {p}}. Remarquons que, si G est abélien, cette classe est réduite à un seul élément.

Nous pouvons alors énoncer le théorème de Chebotarev :

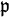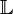Thoérème de Chebotarev —  Soit C une classe de conjugaison dans G. Alors l'ensemble des idéaux premiers \mathfrak {p} de \mathbb {K}, non ramifiés dans \mathbb {L}, et tels que 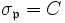\sigma_{\mathfrak {p}} = C, a pour densité naturelle | C | / | G | .

Le théorème de Dirichlet sur les nombres premiers en progression arithmétique en découle trivialement, en appliquant le théorème précédent à une extension cyclotomique de \mathbb{Q}.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de densit%C3%A9 de Chebotarev ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de densite de Chebotarev de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Théorème de densité de chebotarev — Le théorème de Chebotarev généralise, en quelque sorte, le théorème de Dirichlet sur l infinitude des nombres premiers en progressions arithmétiques. Ce dernier stipule que, si sont deux entiers premiers entre eux, la densité naturelle de l… …   Wikipédia en Français

  • Théorème de densité de Chebotarev — En théorie algébrique des nombres, le théorème de Chebotarev généralise, en quelque sorte, le théorème de la progression arithmétique de Dirichlet sur l infinitude des nombres premiers en progression arithmétique. Ce dernier stipule que, si sont… …   Wikipédia en Français

  • Theoreme de la progression arithmetique — Théorème de la progression arithmétique Johann Peter Gustav Lejeune Dirichlet, auteur du théorème En mathématiques, et plus particulièrement en théorie des nombres, le théorème de la progression arithmétique, dû au mathématicien allemand Gustav… …   Wikipédia en Français

  • Théorème de la progression arithmétique — Pour les articles homonymes, voir Théorème de Dirichlet. Johann Peter Gustav Lejeune Dirichlet, auteur du théorème En mathématiques, et plus particulièrement en théorie des nombres, le …   Wikipédia en Français

  • Liste Des Matières De La Théorie Des Nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

  • Liste des matieres de la theorie des nombres — Liste des matières de la théorie des nombres Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 …   Wikipédia en Français

  • Liste des matières de la théorie des nombres — Article détaillé : cryptologie. . Sommaire 1 Facteur (mathématiques) 2 Fractions 3 Arithmétique modulaire 4 Test de primalité e …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”