Lemme De Fatou

Lemme De Fatou

Lemme de Fatou

Le lemme de Fatou est un important résultat dans la théorie de l'intégration de Lebesgue. Il a été démontré par le mathématicien français Pierre Fatou (1878-1929). Ce lemme traite d'un cas où une propriété de convergence simple d'une suite de fonctions conduit à une information sur la limite de l'intégrale de cette suite.

Il est en général présenté dans une suite de trois résultats : d'abord le théorème de convergence monotone, qui sert ensuite à démontrer le lemme de Fatou, puis celui-ci est utilisé pour démontrer le théorème de convergence dominée.

Ce lemme porte parfois le nom de théorème de Fatou-Lebesgue.

Sommaire

Énoncé

Soient 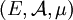(E,\mathcal{A},\mu) un espace mesuré et 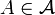A\in\mathcal{A} une partie mesurable de E. On considère 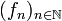(f_n)_{n\in\mathbb{N}} une suite de fonctions mesurables de A à valeur dans l'ensemble des réels positifs 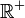\R^+. Si pour tout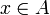 x\in A

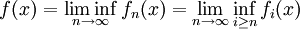
f(x)=\liminf_{n\rightarrow\infty}f_n(x)=\lim_{n\rightarrow\infty}\inf_{i\geq n}f_i(x)

alors la fonction f:A\longrightarrow\overline{\R^+}=[0,+\infty] est mesurable et vérifie :

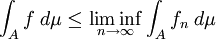\int_A f\;d\mu\leq\liminf_{n\rightarrow\infty}\int_A f_n\;d\mu.

Démonstration

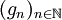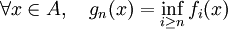Définissons la suite de fonctions (g_n)_{n\in\mathbb{N}} par \forall x\in A,\quad g_n(x)=\inf_{i\geq n}f_i(x).

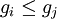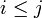Les fonctions gn sont mesurables car définies en tant qu'infimum d'une famille de fonctions mesurables. Par construction g_i\leq g_j si i\leq j donc la suite 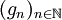(g_n)_{n\in\mathbb{N}} satisfait les hypothèses du théorème de convergence monotone (car elle est positive et croissante), et donc: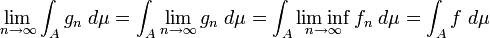

\lim_{n\rightarrow\infty}\int_A g_n\;d\mu=\int_A\lim_{n\rightarrow\infty}g_n\;d\mu=\int_A\liminf_{n\rightarrow\infty}f_n\;d\mu=\int_A f\;d\mu

Or gn est une fonction minorant fi si i est plus grand que n donc

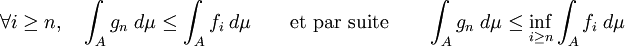\forall i\geq n,\quad\int_A g_n\;d\mu\leq\int_A f_i\;d\mu\qquad\text{et par suite}\qquad\int_A g_n\;d\mu\leq\inf_{i\geq n}\int_A f_i\;d\mu.

Nous avons alors démontré en passant à la limite que:

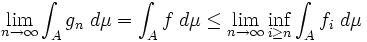\lim_{n\rightarrow\infty}\int_A g_n\;d\mu=\int_A f\;d\mu\leq\lim_{n\rightarrow\infty}\inf_{i\geq n}\int_A f_i\;d\mu.

Voir aussi

Liens internes

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Lemme de Fatou ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Lemme De Fatou de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Lemme de fatou — Le lemme de Fatou est un important résultat dans la théorie de l intégration de Lebesgue. Il a été démontré par le mathématicien français Pierre Fatou (1878 1929). Ce lemme traite d un cas où une propriété de convergence simple d une suite de… …   Wikipédia en Français

  • Lemme de Fatou — Le lemme de Fatou est un important résultat dans la théorie de l intégration de Lebesgue. Il a été démontré par le mathématicien français Pierre Fatou (1878 1929). Ce lemme compare l intégrale d une limite inférieure de fonctions mesurables… …   Wikipédia en Français

  • Fatou (Homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Fatou en Afrique Fatou la Malienne, téléfilm de 2001 Pierre Fatou (1878 1929), mathématicien et astronome Lemme de Fatou, théorème de Fatou Ce document… …   Wikipédia en Français

  • Fatou (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Fatou en Afrique Fatou Diome, écrivaine franco sénégalaise Fatou la Malienne, téléfilm de 2001 Pierre Fatou (1878 1929), mathématicien et astronome Lemme… …   Wikipédia en Français

  • Pierre Fatou — Pour les articles homonymes, voir Fatou (homonymie). Pierre Fatou Mathématicien et Astronome[1 …   Wikipédia en Français

  • Théorème de fatou — Pierre Fatou, mathématicien français (1878 1929) énonça plusieurs théorèmes dont : le Théorème de Fatou (1926) : Soit f une fonction entière qui n est pas une translation. Alors la fonction a un point fixe dans . le Théorème de Fatou… …   Wikipédia en Français

  • Théorème de Fatou —  Ne pas confondre avec le théorème de Fatou Lebesgue (théorème de convergence dominée) ni avec le lemme de Fatou en théorie de l intégration. En mathématiques, le théorème de Fatou est un résultat d analyse complexe dû au mathématicien… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”