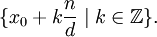Theoreme de congruence lineaire

Theoreme de congruence lineaire

Théorème de congruence linéaire

En arithmétique modulaire, la question des conditions de résolution d'une congruence linéaire peut être résolue par le théorème de congruence linéaire. Si a et b sont des entiers quelconques et n un entier positif, alors la congruence

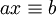ax \equiv b\, (mod n)      (1)

possède une solution si et seulement si le PGCD de (a, n) divise b. Lorsque c'est le cas, et x0 est une solution de (1), alors l'ensemble de toutes les solutions est donné par

\{x_0+k\frac{n}{d}\mid k\in\Bbb{Z}\}.

En particulier, il existera exactement d solutions dans l'ensemble des résidus {0,1,2,...,n-1}.

Exemple

Par exemple, Il n'y a pas d'entier x vérifiant la relation suivante :

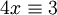4x \equiv 3\, (mod 6)

mais il existe un entier x qui vérifie :

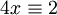4x \equiv 2\, (mod 6).

Autre exemple, l'équation ax ≡ 2 (mod 6) avec différentes valeurs de a donne

3x ≡ 2 (mod 6)

où d = gcd(3,6) = 3 mais puisque 3 ne divise pas 2, il n'existe pas de solution.

5x ≡ 2 (mod 6)

ici d = gcd(5,6) = 1, qui divise b quelconque, et donc il existe simplement une solution dans {0,1,2,3,4,5} : x=4.

4x ≡ 2 (mod 6)

ici d = gcd(4,6) = 2, qui divise 2, et donc il existe exactement deux solutions dans {0,1,2,3,4,5} : x=2 et x=5.

Résoudre une congruence linéaire

Si le PGCD d de a et de n divise b, alors nous pouvons trouver une solution x à la congruence (1) : l'algorithme d'Euclide étendu nous fournit les entiers r et s qui vérifient la relation ra + sn = d. Alors x = rb/d est la solution. Les autres solutions sont les nombres congrus à x modulo n/d.

Par exemple, la congruence

12x ≡ 20 (mod 28)

possède comme solution pgcd (12, 28) = 4, qui divise 20. L'algorithme d'Euclide étendu donne (-2)*12 + 1*28 = 4, ce qui donne r = -2 et s = 1. Par conséquent, la solution est x = -2*20/4 = -10. Toutes les autres solutions sont congrues à -10 modulo 7 : elles sont donc toutes congrues à 4 modulo 7.

Système de congruences linéaires

Par répétition de l'usage du théorème des congruences linéaires, nous pouvons aussi résoudre les systèmes de congruence linéaire, comme dans l'exemple suivant :

Trouver tous les entiers x qui vérifient les relations suivantes :
2x ≡ 2 (mod 6)
3x ≡ 2 (mod 7)
2x ≡ 4 (mod 8)

Par la résolution de la première congruence en utilisant la méthode exposée ci-dessus, nous trouvons x ≡ 1 (mod 3), qui peut être aussi écrit comme x = 3k + 1. En substituant cela dans la deuxième congruence et en simplifiant, nous obtenons

9k ≡ −1 (mod 7)

La résolution de cette congruence fournit k ≡ 3 (mod 7), ou k = 7l + 3. Il s'ensuit ceci x = 3 (7l + 3) + 1 = 21l + 10. En substituant ceci dans la troisième congruence et en simplifiant, nous obtenons

42l ≡ −16 (mod 8)

qui possède la solution l ≡ 0 (mod 4), ou l = 4m. Ceci nous donne x = 21(4m) + 10 = 84m + 10, ou

x ≡ 10 (mod 84)

qui donne toutes les solutions de ce système.

Article détaillé : Théorème des restes chinois.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de congruence lin%C3%A9aire ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de congruence lineaire de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Théorème de congruence linéaire — En arithmétique modulaire, la question des conditions de résolution d une congruence linéaire peut être résolue par le théorème de congruence linéaire. Si a et b sont des entiers quelconques et n un entier positif, alors la congruence (mod… …   Wikipédia en Français

  • Theoreme des deux carres de Fermat — Théorème des deux carrés de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de… …   Wikipédia en Français

  • Théorème de Fermat sur les sommes de deux carrés — Théorème des deux carrés de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de… …   Wikipédia en Français

  • Théorème des deux carrés — de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons… …   Wikipédia en Français

  • Théorème des deux carrés de fermat — Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons différentes il peut …   Wikipédia en Français

  • Théorème des deux carrés de Fermat — Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons différentes il peut …   Wikipédia en Français

  • Fonction linéaire — Dans les mathématiques élémentaires, les fonctions linéaires sont les fonctions les plus simples que l on rencontre. Ce sont des cas particuliers d applications linéaires. Elles traduisent la proportionnalité. Par exemple, on dira que le prix d… …   Wikipédia en Français

  • Generateur congruentiel lineaire — Générateur congruentiel linéaire Un générateur congruentiel linéaire est un générateur de nombres pseudo aléatoires dont l algorithme, introduit en 1948 par D.H Lehmer, sous une forme réduite, pour produire des nombres aléatoires, est basé sur… …   Wikipédia en Français

  • Générateur Congruentiel Linéaire — Un générateur congruentiel linéaire est un générateur de nombres pseudo aléatoires dont l algorithme, introduit en 1948 par D.H Lehmer, sous une forme réduite, pour produire des nombres aléatoires, est basé sur des congruences et une fonction… …   Wikipédia en Français

  • Générateur congruentiel linéaire — Un générateur congruentiel linéaire est un générateur de nombres pseudo aléatoires dont l algorithme, introduit en 1948 par D.H Lehmer, sous une forme réduite, pour produire des nombres aléatoires, est basé sur des congruences et une fonction… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”