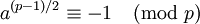Theoreme de Proth
- Theoreme de Proth
-
Théorème de Proth
En mathématiques, le théorème de Proth en théorie des nombres est un test de primalité pour les nombres de Proth.
Ce théorème énonce que pour un nombre de Proth p, donc de la forme k2n + 1 avec k un naturel impair et k < 2n, s'il existe un entier a tel que :
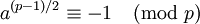
alors p est premier.
Ce test est pratique car si p est premier, un a choisi a environ 50% de chances de prouver la primalité de p. De plus il est remarquablement utile pour démontrer la conjecture de Sierpinski.
Exemples numériques
Les sept premiers nombres de Proth correspondent à suite A080075 de l’OEIS:
- P0 = 21 + 1 = 3
- P1 = 22 + 1 = 5
- P2 = 23 + 1 = 9
- P3 = 3 × 22 + 1 = 13
- P4 = 24 + 1 = 17
- P5 = 3 × 23 + 1 = 25
- P6 = 25 + 1 = 33
Exemples du théorème :
- Pour p = 3, 21 + 1 = 3 ce qui est divisible par 3 ; donc 3 est premier.
- Pour p = 5, 32 + 1 = 10 ce qui est divisible par 5 ; donc 5 est premier.
- Pour p = 13, 56 + 1 = 15626 ce qui est divisible par 13 ; donc 13 est premier..
- Pour p = 9, qui n'est pas premier, il n'existe pas de a tel que a4 + 1 soit divisible par 9.
Histoire
- Le mathématicien François Proth (1852 - 1879) découvrit le théorème en 1878.
Voir aussi
Liens externes
 Portail des mathématiques
Portail des mathématiques
Catégories : Test de primalité | Théorème de mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Proth de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème de proth — En mathématiques, le théorème de Proth en théorie des nombres est un test de primalité pour les nombres de Proth. Ce théorème énonce que pour un nombre de Proth p, donc de la forme k2n + 1 avec k un naturel impair et k < 2n, s il existe un… … Wikipédia en Français
Théorème de Proth — En mathématiques, le théorème de Proth en théorie des nombres est un test de primalité pour les nombres de Proth. Ce théorème énonce que pour un nombre de Proth p, donc de la forme k2n + 1 avec k un naturel impair et k < 2n, s il existe un… … Wikipédia en Français
Nombre de Proth — En théorie des nombres, un nombre de Proth est un nombre de la forme où k est un nombre impair, n un entier positif, et 2n > k. Les nombres de Proth sont nommés ainsi d après le mathématicien François Proth (en). Si un nombre de … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… … Wikipédia en Français
Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français
Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème … Wikipédia en Français