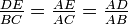Thalès de Milet

Pour les articles homonymes, voir Thalès (homonymie).

Thalès

Naissance	-625 Milet (Anatolie)
Décès	-547 Milet (Anatolie)
Champs	Mathématiques, Philosophie
Institution	École milésienne
Célèbre pour	Théorème de Thalès
modifier

Thalès de Milet appelé communément Thalès (en grec ancien Θαλής / Thalês), était un philosophe présocratique ionien né à Milet vers -625 et mort vers l'an 547 av. J.-C. Il fut l'un des Sept sages de la Grèce et le fondateur présumé de l'école milésienne.

Biographie

Thalès de Milet est considéré comme le premier philosophe, scientifique et mathématicien grec. Il est aussi vu comme un homme politique, si l'on tient compte de sa participation au groupe des « Sept Sages ». Il a eu une première femme nommée Cléfitis, puis une seconde femme nommée Apolide.

Le situer dans le temps est difficile même si l'on tient compte de la date de l'éclipse de soleil qu'il aurait supposément prédite^[1]. Mais Diogène Laërce situe sa mort à la 58^e olympiade (548-545 av. J.-C.).

La vie de Thalès a manifestement subi un processus d'idéalisation, et ce que nous connaissons de ce penseur, comme pour les autres Présocratiques, nous renseigne surtout sur le type commun du sage en Grèce. Rapportant les dires d'Hérodote, Diogène raconte que Thalès serait le fils d'Examios, un marchand, et de Cléobuline^[2]. On entend parfois qu'il descendait de la famille des Thélides, des rois mythiques de Phénicie de la lignée d'Agénor et de Cadmos. Plusieurs autres sources affirment pourtant qu'il était peut-être d'origine béotienne ou phénicienne et probablement contemporain de Solon et de Crésus et qu'il se serait installé à Milet en compagnie de son ami Neileôs. Il n'est donc pas sûr que Thalès soit Milésien, quoiqu'une tradition courante fasse de lui un descendant d'une famille aisée de Milet. Cependant, il faut insister sur le fait que les sources les plus fiables et complètes proviennent de Diogène Laërce et d'Hérodote.

Il commença pourtant sa vie comme simple commerçant puis s'orienta vers une carrière politique et économique.

En ce qui concerne sa carrière politique, voici ce que rapporte Diogène Laërce : « Il paraît aussi avoir été un éminent conseiller politique. Ainsi marqua-t-il son opposition, quand Crésus envoya une ambassade proposer aux Milésiens de s'engager à ses côtés; étant donné ensuite la victoire de Cyrus, ce refus assura la survie de la Cité. » Cette réputation lui permit de convaincre les cités-États (ou polis) d'Ionie de se regrouper en fédération^[3]. Thalès le scientifique ne doit donc pas occulter un autre Thalès, habile en affaires et prompt à dénigrer ses propres découvertes et sa fortune acquise. Il connut d'abord sa renommée comme conseiller militaire et comme ingénieur. Durant la guerre entre les Perses et les Lydiens, il aurait détourné le cours du fleuve Halys pour faire passer l'armée de Crésus^[4].

Il s'embarqua un jour vers Naucratis (Égypte actuelle), ville reconnue pour sa culture scientifique. Il y étudia les mathématiques, particulièrement la géométrie où il fit déjà quelques découvertes^[5]. Il fut un des créateurs de la physique, de la géométrie et de l’astronomie.

On prétend qu'il se passionnait de gymnastique et qu'on l'aurait trouvé dans les gradins, mort par déshydratation lors d'une compétition à laquelle il assistait. Diogène Laërce nous relate sa mort de manière émouvante :

« Thalès le Sage mourut en assistant à une rencontre sportive, du fait de la faim, de la soif, et de la faiblesse de l'âge». On grave sur son tombeau :

« Petit est ce tombeau, mais au ciel va sa gloire.
Regarde, c'est celui de Thalès, grand esprit. »

Nous-mêmes avons composé sur lui l'épigramme suivante, éditée au premier livre de nos Epigrammes et mètres divers :

« Tandis qu'il contemplait une lutte sportive,
Zeus Solaire, tu as, hors du stade, ravi
Thalès dont la sapience avait fait le renom.
Je te loue de l'avoir rappelé près de toi,
Car il était très vieux, et depuis cette terre,
La force lui manquait pour observer les astres. »

Sagesse

Voici une anecdote intéressante rapportée par Diogène Laërce et reprise par Platon dans le Théétète (174 a), qui illustre bien l'intérêt de Thalès pour l'étude des astres :

Socrate : L’exemple de Thalès te le fera comprendre, Théodore. Il observait les astres et, comme il avait les yeux au ciel, il tomba dans un puits. Une servante de Thrace, fine et spirituelle, le railla, dit-on, en disant qu’il s’évertuait à savoir ce qui se passait dans le ciel, et qu’il ne prenait pas garde à ce qui était devant lui et à ses pieds. La même plaisanterie s’applique à tous ceux qui passent leur vie à philosopher. Il est certain, en effet, qu’un tel homme ne connaît ni proche, ni voisin ; il ne sait pas ce qu’ils font, sait à peine si ce sont des hommes ou des créatures d’une autre espèce ; mais qu’est-ce que peut être l’homme et qu’est-ce qu’une telle nature doit faire ou supporter qui la distingue des autres êtres, voilà ce qu’il cherche et prend peine à découvrir. Tu comprends, je pense, Théodore ; ne comprends-tu pas^[6] ?

Théories

Cosmologie

Thalès est donc le premier « penseur » connu de l'histoire. Sa philosophie de la nature fait de l'eau le principe explicatif de l'univers, d'où procèdent les autres éléments, air, feu et terre. Accordant une vitalité à cette matière unique et universelle, il estime que l'eau est le principe de toutes choses, que la Terre n’est que de l’eau condensée, l’air de l’eau raréfiée, et qu’en dernière analyse tout se résolvait en eau :

« Thalès, le fondateur de cette manière de philosopher, prend l'eau pour principe, et voilà pourquoi il a prétendu que la terre reposait sur l'eau, amené probablement à cette opinion parce qu'il avait observé que l'humide est l'aliment de tous les êtres, et que la chaleur elle-même vient de l'humide et en vit ; or, ce dont viennent les choses est leur principe. C'est de là qu'il tira sa doctrine, et aussi de ce que les germes de toutes choses sont de leur nature humides, et que l'eau est le principe des choses humides. Plusieurs pensent que dès la plus haute antiquité, bien avant notre époque, les premiers théologiens ont eu la même opinion sur la nature : car ils avaient fait l'Océan et Téthys auteurs de tous les phénomènes de ce monde, et ils montrent les dieux jurant par l'eau que les poètes appellent le Styx. En effet, ce qu'il y a de plus ancien est ce qu'il y a de plus saint ; et ce qu'il y a de plus saint, c'est le serment. Y a-t-il réellement un système physique dans cette vieille et antique opinion ? C'est ce dont on pourrait douter. Mais pour Thalès on dit que telle fut sa doctrine.^[7] »

— Aristote, Métaphysique, A, III, 983 ; trad. Victor Cousin, 1838

Cet élément primitif est d'origine incertaine, peut-être phénicienne.

« La conception de Thalès : une terre flottante, comme un disque de bois, sur l'eau ; et un univers rempli de matière primordiale, c'est-à-dire envisagé comme une masse liquide, s'accorde, comme le fait voir Tannery, Pour l'histoire de la science hellène, pp. 70 sq., en une certaine mesure avec l'idée égyptienne de l'eau primordiale Nun, divisée en deux masses séparées. Les anciens Babyloniens admettaient pareillement un Océan supérieur et un Océan inférieur; cf. Fritz Hommel, Der babylonische Ursprung der aegyptischen Kultur, Munich 1892, p. 8. On peut comparer aussi avec le livre de la Genèse, I 7. La concordance entre la doctrine fondamentale de Thalès et celle de la secte mi juive des Sampséens reste tout à fait obscure ; cf. Hilgenfeld, Judentum und Judenchristentum, p. 98, d'après Epiphan. Haeres, 19, 1 ; cf. aussi Plutarque, sur les Syriens, Quaest. conviv., VIII 8, 4 (Mor., 891, 7 sq., Dübner). La tendance actuelle est de considérer Thalès comme un simple intermédiaire entre étrangers et Grecs ; cette tendance a pourtant contre elle la façon dont la meilleure autorité, Eudème, op. cit., parle des travaux géométriques de Thalès et du rapport dans lequel ils se trouvent avec la mathématique égyptienne. »

— Theodor Gomperz, Les Penseurs de la Grèce : histoire de la philosophie antique, tome I, livre I, chapitre 1, II

La raison de ce choix pour l'eau provient sans doute de l'importance de celle-ci dans la croissance et la nutrition des choses vivantes, de son rôle central dans le quotidien des Milésiens et des observations qu'on prétend qu'il a faites en Égypte quant à l'importance du Nil et des autres fleuves qui faisaient l'objet de cultes. Mais l'originalité de Thalès est de faire de cette explication mythologique un principe de connaissance physique et métaphysique ; en effet, l'unité de l'élément eau est aussi l'unité du monde : « Thalès et son école : le monde est un », Aetius.

Cette thèse est une grande innovation, car elle suppose l'affirmation de vérités, non à partir de quelques objets singuliers, comme c'était le cas avant lui pour les Égyptiens ou les Babyloniens, mais pour une infinité d'objets contenus dans le monde et pour le monde lui-même. Il énonce donc des vérités concernant une classe entière d'êtres. Ainsi, selon l'helléniste allemand Zeller (XIX^e siècle), l'apport majeur de Thalès est d'avoir généralisé et conceptualisé ses observations, d'être parvenu au concept de l'un sans se perdre dans l'accumulation d'observations disparates. C'est là la thèse fondamentale de ce philosophe dont nous ne connaissons rien avec certitude. On attribue parfois à Thalès une conception de l'univers assez séduisante : celui-ci serait un genre de bulle d'air hémisphérique formée par la concavité du Ciel et la surface plane de la Terre, qui flotte elle-même sur l'eau. Le mouvement de la Terre sur l'eau expliquerait les tremblements de terre^[8].

Il savait aussi tirer profit de ses observations. Aristote^[9] raconte que Thalès, prévoyant une abondante récolte d'olives, aurait monopolisé les pressoirs pour mieux monnayer leurs services ; il voulait ainsi montrer que le sage est capable de faire fortune mais qu'il ne s'en préoccupe pas, préférant la contemplation, la recherche scientifique et la vie honnête.

Mathématiques

Théorème de Thalès :

Diogène Laërce, dans Vies, Doctrines et sentences des philosophes illustres, vol. 1, précise que Hiéronyme dit que Thalès mesura les pyramides d'Égypte en calculant le rapport entre leur ombre et celle de notre corps. L'anecdote rapporte que le Pharaon Amasis aurait mis ses connaissances à l'épreuve en lui disant que personne n'était en mesure de savoir quelle était la hauteur de la Grande Pyramide^[10].

Il partit simplement du principe qu'à un certain moment de la journée, l'ombre de tout objet devient égale à sa hauteur. Il ne lui restait qu'à déterminer le moment exact. Il devait également pour cela tenir compte de ce que les rayons du soleil devaient être perpendiculaires avec l'un de ses côtés, ce qui ne se produisait que deux fois par année (21 novembre et le 20 janvier)^[11]. La raison de cela est que la pyramide de Khéops se trouve à Gizeh (30° de latitude dans l'hémisphère nord) et pour que l'ombre soit égale à l'objet, il faut que les rayons solaires soient inclinés à 45°. De plus, pour que l'ombre soit perpendiculaire à la base, elle doit être orientée nord-sud. Par la suite, Thalès se servit de sa propre taille comme unité de mesure. Il obtint les résultats suivants : 18 thalès pour l'ombre, puis il mesura le côté de la base qu'il divisa par deux et obtint 67 thalès ; la pyramide de Khéops mesure alors 85 Thalès. Or en mesure locale, le Thalès valait 3,25 coudées égyptiennes, ce qui fait 276,25 coudées au total. Nous savons aujourd'hui que la hauteur de la pyramide de Khéops est de 280 coudées soit 147 mètres. Comme quoi, la mesure de Thalès était déjà passablement précise. Impressionnés par ce calcul, les prêtres lui donnèrent accès à la bibliothèque où il put consulter de nombreux ouvrages d'astronomie.

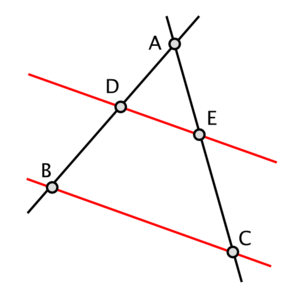
Son nom est célèbre par le fameux théorème de Thalès (qu'il ne connaissait pas), qui donne des relations entre les rapports de distances de triangles. La première démonstration de ce théorème est attribuée à Euclide qui la présente dans ses Éléments, dans le Livre VI (Proposition 2) — il le démontre par proportionnalité d'aires de triangles de hauteur égale.

Les historiens lui attribuent toutefois cinq théorèmes de géométrie élémentaire :

1. Un cercle est partagé en deux parties égales par tout diamètre.
2. Les angles à la base d'un triangle isocèle sont égaux.
3. Les angles opposés par le sommet sont égaux.
4. Deux triangles sont égaux s'ils ont deux angles et le côté compris égaux.
5. Un angle inscrit dans un demi-cercle est droit.

Astronomie

Son intérêt pour l'astronomie le poussa à faire de nombreuses observations sur les constellations. Il aurait été le premier à noter le voyage du soleil entre les deux Tropiques. Il établit aussi que certaines étoiles n'étaient pas toutes fixes par rapport aux autres et il les baptisa « Planètes », ce qui signifie corps errant. On dit même qu'il parvint à en répertorier les éphémérides. Il fut aussi le premier à constater que l'année ne comptait pas 365 jours, mais 365 et un quart.

On rapporte qu'il prédit l'éclipse de soleil du 27 mai 584 av. J.-C. [1] Mais cette assertion relève très certainement de la légende^[12]. En effet, à cette époque, la prédiction des éclipses lunaires était relativement connue puisqu'elles se répètent sur un cycle de dix-neuf ans (Saros). Une éclipse lunaire est également visible de toute la partie de la Terre orientée vers la Lune. Mais il en va autrement pour les prédictions des éclipses solaires qui ne sont visibles que pendant quelques minutes sur une portion réduite du globe terrestre, et Thalès n'avait pas les connaissances requises pour faire de telles prévisions. Cela demande non seulement des moyens géométriques puissants mais aussi des calculs trigonométriques complexes, ainsi que des tables très élaborées, construites à partir d'éphémérides anciennes. Tous ces moyens ne seront à la disposition des astronomes que plusieurs siècles plus tard (cf sciences grecques). Les Babyloniens possédaient certes des éphémérides remontant au moins au VIIIe siècle, mais les autres éléments leur manquaient. Quoi qu'il en soit, quand l'éclipse se produisit, les Mèdes et les Lydiens alors en guerre furent pris d'une panique telle qu'ils conclurent un accord de paix.

C'est en son temps que remonte la connaissance de l'électricité puisqu'il savait déjà que l'ambre avait la propriété d'attirer les matériaux légers. Suite à ces expériences, le mot « électricité » (ηλεκτρον en grec ancien) est donné en référence à l'ambre jaune. Il est considéré comme un des créateurs de la physique, de la géométrie et de l’astronomie : Il décrivit la Grande Ourse et conseilla aux marins de s’en servir pour se guider, calcula la durée de l’année et des intervalles des solstices aux équinoxes, évalua le diamètre apparent du soleil et les grandeurs relatives de cet astre et la lune.

L'école de Milet

De retour à Milet, il fonda l'École milésienne. On sait qu'Anaximandre et Anaximène furent ses successeurs. Mais nous n'avons aucun écrit de lui, et nous ne savons pas même s'il écrivit jamais. Il est difficile de préciser ses idées et d'être assuré de certaines de ses découvertes scientifiques. On sait cependant que dans cette école, il aurait prononcé la formule désormais célèbre : « Connais-toi toi-même. »

L'école de Milet réalise deux grandes avancées fondatrices :

• la première est la distinction entre le naturel et le surnaturel. Loydd écrit ainsi que « les Milésiens laissent les dieux à la porte ». De façon plus exacte, ils ne chassent pas le divin de la connaissance du monde, mais la Mythologie, en cherchant des causes naturelles aux phénomènes. Ce changement d'attitude fait succéder l'explication naturaliste à l'explication divine classique.
• la seconde en découle naturellement par la recherche de la véracité : les Milésiens mettent en place la discussion des arguments défendus. Admettre la discussion scientifique est une nécessité de l'avancée scientifique et une qualité de la rationalité.

Citations/Apophtegmes

• « Difficile de se connaître soi même. »
• « Ce qui est sûr c'est ce qui est arrivé, personne ne sait ce qui arrivera. »
• « Entoure toi de gens capables. »
• « Le besoin est puissant, il vainc tout. »
• « Mieux vaut faire envie que pitié. »
• « Le temps est sage, il révèle tout. »
• « Ne dis pas que tu as l'intention de faire quelque chose car si tu échoues, tous riront de toi. »
• « Qui est heureux : l'homme bien portant, riche, courageux et instruit. »

Sponde, praesto noxa est ; Amicorum praesentium et absentium memento ; Faciem ne ornato, sed studiis honestis ornatissimus esto ; Noli male ditescere ; Cave sermo tuus invisum te faciat iis qui fide interposita earundem rerum socii sunt ; parentibus blandiri ne dubita ; Maleficium ne admitte ; Qualia parentibus praemia dederis, talia ipse senex a liberis tuis exspecta ; Difficile est noscere bonum ; Suavissimum est optatis potiri ; Desidia res molesta est ; Malum intemperantia ; Ignorantia incommoda est ; Doce ac disce meliora ; Noli otiari, etiamsi dives sis ; Res secundas cela invidiae declinandae causa ; Fac ne miserabilis fias ; Modum adhibe ; Cave omnibus credas ; Quum imperas, rege te ipsum.

Bibliographie

Sources

• Hérodote, Histoires [détail des éditions] [lire en ligne] (I, 74-75 et 170 ; II, 20 et 109)
• Platon
  • Théétète, 174 a
  • Protagoras, 343 a
• Aristote
  • Politique I, XI, 1259 a 6 [8] - [13]
  • Métaphysique, A, III, 983 b 6
  • Traité du ciel, II, XIII, 294 a, 28
  • De l'âme, I, V, 411 a 7 et I, II, 405 a 19
• Scolie à Platon, République, X, 600a
• Callimaque, Iambes, fr. 94
• Clément d'Alexandrie, Stromates [(en) lire en ligne], I, 65
• Tatien, Discours aux Grecs, 41
• Eusèbe, Chronographie, Contre Julien
• Cicéron
  • De la divination [détail des éditions] [lire en ligne], I, 49, 111, 112
  • De la nature des Dieux [détail des éditions] [lire en ligne], I, X, 25
• Sénèque, Questions naturelles [lire en ligne], III, 13 et 14, IV, 2, 22 ; VI, 6, 1
• Plutarque
  • Vies parallèles [détail des éditions] [lire en ligne], Solon, 2 ; 12
  • Isis et Osiris, 34
  • Le Banquet des Sept Sages, 2
  • Pourquoi la prophétesse Pythie ne rend plus les oracles en vers, 18, 402, E
• Diogène Laërce, Vies, doctrines et sentences des philosophes illustres [détail des éditions] [lire en ligne], I, 22-40
• Pline l'Ancien, Histoire naturelle [détail des éditions] [lire en ligne], II, 53, XVIII, 213, XXXVI, 82
• Proclus, Commentaire sur le premier livre d'Euclide, 65, 3
• Flavius Josèphe, Contre Apion, I, 2
• Aetius, Opinions, I, III, I
• Souda [(en)(grc) lire en ligne]
• Jamblique, Vie pythagorique, 12
• Simplicius, Commentaire sur la Physique d'Aristote, 23, 21 et 458, 23
• Apulée, Florides, 18
• Julien, Discours, III, 162, 2
• Galien, Sur les humeurs d'Hippocrate, I, I
• Ausone, Le Jeu des Sept Sages
• Hesychius

Fragments et témoignages

• Giorgio Colli, Sagesse grecque : Épiménide, Phérécyde, Thalès, Anaximandre, Tome 2, Éclat éds, 1992 (ISBN 2905372532).
• Jean-Paul Dumont, Les Présocratiques, Gallimard, coll. « Bibliothèque de la Pléiade », 1988 (ISBN 2070111393).
• trad. John Burnet en ligne [2]

Études

• P. Tannery, Thalès et ses emprunts à l'Égypte [lire en ligne].
• Theodor Gomperz, Les Penseurs de la Grèce : histoire de la philosophie antique [lire en ligne] (tome I, livre I, chapitre 1, II).
• Robert Lahaye, La Philosophie ionienne. L'École de Milet, éd. du Cèdre, Paris, 1966.
• Geoffrey Lloyd, Les Débuts de la science grecques — De Thalès à Aristote, La Découverte, 1990 (ISBN 2707119431).

Notes et références

Voir aussi

Articles connexes

• Cosmologie
• Figure de la Terre dans l'Antiquité
• Sciences grecques
• Théorème de Thalès

Liens externes

• (fr) La leçon de Thalès, Sur le sens des premières cosmologies
• (en) Thalès, article de The Internet Encyclopedia of Philosophy

• Portail de la philosophie antique
• Portail de la Grèce antique
• Portail des mathématiques
• Portail de l’astronomie
• Portail de la géodésie et de la géophysique

La version du 6 septembre 2005 de cet article a été reconnue comme « article de qualité » (comparer avec la version actuelle). Pour toute information complémentaire, consulter sa page de discussion et le vote l’ayant promu. La version du 6 septembre 2005 de cet article a été reconnue comme « article de qualité », c'est-à-dire qu'elle répond à des critères de qualité concernant le style, la clarté, la pertinence, la citation des sources et l'illustration.