- Tests de normalité
-
Test de normalité
En statistiques, les tests de normalité permettent de vérifier que des données réelles suivent une loi normale ou non. Les tests de normalité sont des cas particuliers des tests d'adéquation (ou tests d'ajustement, tests permettant de comparer des distributions), appliqués à une loi normale.
Ces tests prennent un place importante en statistiques. En effet, de nombreux tests supposent la normalité des distributions pour être applicable. En toute rigueur, il est indispensable de vérifier la normalité avant d'utiliser les tests. Cependant, de nombreux tests sont suffisamment robuste pour être utilisable même si les distributions s'écartent de la loi normale.
Sommaire
Approches empiriques et graphiques
Histogramme de la distribution
Il est possible de visualiser la forme de la distribution des données à analyser en les représentant sous forme d'histogramme puis de comparer la forme de cette histogramme avec une courbe représentant une loi normale (les paramètres de cette loi étant calculés à partir des données à analyser). Ceci ne permet pas de conclure à la normalité des données mais peut donner un idée du type de loi sous-jacente : loi normale, loi de Cauchy ou loi de Student si la distribution semble symétrique, loi log-normale, loi gamma, loi de Weibull, loi exponentielle ou loi bêta si la distribution est asymétrique.
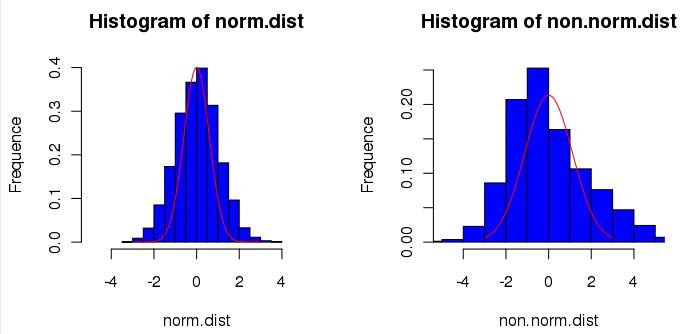
- layout(matrix(1:2, 1, 2))
- # Distribution normale
- norm.dist <- rnorm(5000)
- hist(norm.dist, nclass=20, ylab="Frequence", xlim=c(-5,5), pro=T, col="blue")
- lines(seq(-3,3,le=100), dnorm(seq(-5,5,le=100), 0, sqrt(var(norm.dist))), col="red")
- # Distribution non normale
- non.norm.dist <- c(rnorm(5000, -1), rnorm(5000, 1, 2))[sample(10000, size=5000)]
- hist(non.norm.dist, nclass=20, ylab="Frequence", xlim=c(-5,5), pro=T, col="blue")
- lines(seq(-3,3,le=100), dnorm(seq(-5,5,le=100), 0, sqrt(var(non.norm.dist))), col="red")
Histogramme des résidus
Il est également possible de représenter l'histogramme des résidus(c'est-à-dire la différence entre la distribution observée et la loi normale). Les résidus doivent suivre également un loi normale.
- layout(matrix(1:6, 2, 3, byrow=T))
- # Distribution normale
- norm.dist <- rnorm(1000)
- plot(norm.dist, col="blue")
- abline(0, 0, col="red")
- hist(norm.dist, nclass=50, ylab="Frequence", xlim=c(-5,5), pro=T, col="blue")
- lines(seq(-3,3,le=100), dnorm(seq(-5,5,le=100), 0, sqrt(var(norm.dist))), col="red")
- qqnorm(norm.dist)
- qqline(norm.dist, col="red")
- # Distribution non normale
- non.norm.dist <- c(rnorm(10000, -1), rnorm(1000, 1, 2))[sample(2000, size=1000)]
- plot(non.norm.dist, col="blue")
- abline(0, 0, col="red")
- hist(non.norm.dist, nclass=50, ylab="Frequence", xlim=c(-5,5), pro=T, col="blue")
- lines(seq(-3,3,le=100), dnorm(seq(-5,5,le=100), 0, sqrt(var(non.norm.dist))), col="red")
- qqnorm(non.norm.dist)
- qqline(non.norm.dist, col="red")
Boîte à moustaches (box-plot)
Une boîte à moustaches permet de visualiser rapidement la symétrie de la distribution des données réelles et la présence de valeurs atypiques.
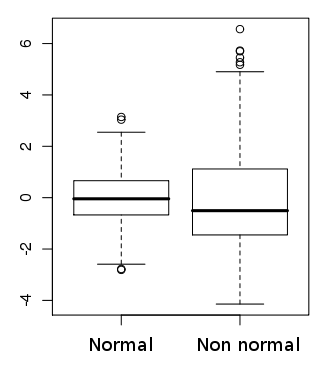
- norm.dist <- rnorm(500)
- non.norm.dist <- c(rnorm(500, -1), rnorm(500, 1, 2))[sample(1000, size=500)]
- boxplot(norm.dist, non.norm.dist)
Graphe quantile-quantile (qq-plot)
Coefficients d'asymétrie et d'aplatissement
Les Coefficients d'asymétrie et d'aplatissement sont également utiles pour définir une loi normale.
Pour l'aplatissement :
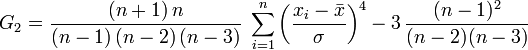
et pour l'asymétrie :
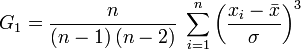
avec σ un estimateur non biaisé de la variance.
On sait effectivement que le coefficient d'asymétrie vaut zéro pour toute loi normale, tandis que le coefficient d'aplatissement vaut 3 (0 si normalisé)
Approche probabiliste
Il existe également un grand nombre de tests de normalité:
- Tests basés sur la fonction de répartition empirique : Test de Kolmogorov-Smirnov et son adaptation le test de Lilliefors (en), ou le test de Anderson-Darling (en) et le test de Cramer–Von Mises (en)
- Tests basés sur les moments, comme le Test de Jarque Bera ou test D'Agostino's K-squared (en)
- ou encore le test de Shapiro-Wilk (en), ou le test de Shapiro–Francia.
Généralités
Les tests de normalité sont des tests d'hypothèse. En notant F(x) la fonction de répartition basée sur les données à analyser et F0(x) la fonction de répartition théorique, les hypothèses nulle et alternative peuvent s'écrire :
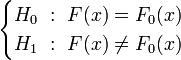 .
.Les tests sur les moments ont une hypothèse moins forte, ils ne testent pas si la fonction de répartition est normale, mais si les moments (coefficients d'asymétrie et d'aplatissement) de la distribution inconnue sont identiques à ceux d'une loi normale:
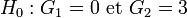
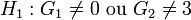
On remarquera que ce n'est pas suffisant pour caractériser une loi normale (Problème des moments).
Test d'adéquation du χ²
Article détaillé : Test du χ².Son utilisation n'est pas recommandé du fait de son manque de puissance et de la nécessité de diviser les distributions en classes.
[1].
Tests bayesien
Kullback-Leibler distances between the whole posterior distributions of the slope and variance do not indicate non-normality. However, the ratio of expectations of these posteriors and the expectation of the ratios give similar results to the Shapiro-Wilk statistic except for very small samples, when non-informative priors are used.[2]
Spiegelhalter suggests using Bayes factors to compare normality with a different class of distributional alternatives.[3] This approach has been extended by Farrell and Rogers-Stewart.[4]
Applications
One application of normality tests is to the residuals from a linear regression model. If they are not normally distributed, the residuals should not be used in Z tests or in any other tests derived from the normal distribution, such as t tests, F tests and chi-square tests. If the residuals are not normally distributed, then the dependent variable or at least one explanatory variable may have the wrong functional form, or important variables may be missing, etc. Correcting one or more of these systematic errors may produce residuals that are normally distributed.
Voir aussi
- (fr) Gilbert Saporta, Probabilités, Analyse des données et Statistique, 2006 [détail des éditions] (p. 359 à 370).
- Judge et al., Introduction to the Theory and Practice of Econometrics, Second Édition, 1988; 890–892.
- Gujarati, Damodar N., Basic Econometrics, Fourth Édition, 2003; 147–148
Références
- ↑ Judge et al. (1988) and Gujarati (2003) recommendent le test de Jarque–Bera.
- ↑ Young K. D. S. (1993), Bayesian diagnostics for checking assumptions of normality. Journal of statistical computation and simulation, vol. 47, no3-4, pp. 167-180
- ↑ Spiegelhalter, D.J. (1980). An omnibus test for normality for small samples. Biometrika, 67, 493-496. DOI:10.1093/biomet/67.2.493
- ↑ Farrell, P.J., Rogers-Stewart, K. (2006) Comprehensive study of tests for normality and symmetry: extending the Spiegelhalter test. Journal of Statistical Computation and Simulation, 76(9), 803 – 816. DOI:10.1080/10629360500109023
Liens externes
- Cours de statistique de R. Rakotomalala - Tests de normalité.
- Exemple pratique de tests de normalité dans Tanagra.
- Informations sur les tests de normalité de la librairie nortest de R.
- Tester l'adéquation à la loi normale.
- Portail des probabilités et des statistiques
Catégorie : Test statistique
Wikimedia Foundation. 2010.
