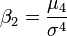- Coefficient d'aplatissement
-
Kurtosis
En théorie des probabilités et en statistiques, le kurtosis (mot d'origine grec ), plus souvent traduit par coefficient d'aplatissement, ou coefficient d'aplatissement de Pearson, correspond à une mesure de l'aplatissement, ou a contrario de la pointicité, de la distribution d'une variable aléatoire réelle. C'est la seconde des caractéristiques de forme, avec le coefficient de dissymétrie. Elle mesure, hors effet de dispersion (donnée par l'écart-type), la disposition des masses de probabilité autour de leur centre, tel que donné par l'espérance mathématique, c'est-à-dire d'une certaine façon, leur regroupement proche ou loin du centre de probabilité.
Sommaire
Définition
On le définit, sous réserve que les moments impliqués existent, comme :
En français explicite, c'est le rapport entre le moment centré d'ordre 4 et le carré du moment centré d'ordre 2 (appelé variance).
Pour une distribution de probabilité quelconque, ce coefficient est compris entre 1 et +∞. Pour une distribution de probabilité suivant la loi normale centrée réduite, ce coefficient d'aplatissement vaut 3.
Un coefficient d'aplatissement élevé indique que la distribution est plutôt pointue en sa moyenne, et des queues de distribution épaisses (fat tails en anglais). Ceci s'intuite par l'approche alternative suivante : en effet, une autre manière d'exprimer ce coefficient est de considérer les contributions élémentaires au moment d'inertie de la variable aléatoire ; notons cette dernière X. Cela revient à s'intéresser à la distribution de
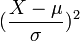(notations classiques). En moyenne ce paramètre vaut 1, par construction. Son moment d'ordre 2 est le coefficient d'aplatissement. Comme son espérance mathématique est fixée, son moment d'ordre 2 ne peut évoluer que par compensation : pour l'augmenter, il faut de l'inertie en position éloignée, contrebalancée par de l'inertie proche. Du point de vue typologie, si β2 > 3, on parle de distribution leptokurtique. La notion de leptokurtosis est très utilisée dans le milieu de la finance de marché, les échantillons ayant des queues plus épaisses que la normale aux extrémités, impliquant des valeurs anormales plus fréquentes[1]À l'opposé, un coefficient d'aplatissement proche de un indique une distribution relativement aplatie pour une même variance. Si β2 < 3, on parlera de distribution platikurtique.
Et pour boucler cet aspect de typologie, si β2 = 3, on parle de distribution mésokurtique.
L'excès d'aplatissement
On normalise parfois le coefficient d'aplatissement en lui soustrayant la valeur correspondant à la loi normale centrée réduite, à savoir 3 :
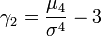.Cet excès d'aplatissement, kurtosis excess en anglais, est source d'ambiguïté. Avec cette nouvelle acception, un excès d'aplatissement positif correspond à une distribution pointue et un excès d'aplatissement négatif à une distribution aplatie. Un excès d'aplatissement nul correspond à une distribution quasi-normale, d'autant mieux qu'elle sera symétrique (coefficient d'asymétrie proche de 0).
Estimateur non biaisé
Les définitions théoriques β2 et γ2 du coefficient d'aplatissement sont des mesures biaisées. Plusieurs logiciels de statistiques (SAS, Tanagra, Minitab, PSPP/SPSS et Excel par exemple) utilisent un estimateur non biaisé pour la loi normale :
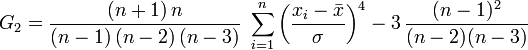
avec σ un estimateur non biaisé de la variance.
Articles connexes
Notes et références
- ↑ Régis Bourbonnais & Michel Terraza, Analyse des séries temporelles, 2e édition, Dunod, 2008, p. 296
Portail des probabilités et des statistiques
Catégorie : Statistique descriptive
Wikimedia Foundation. 2010.
