Série de laurent

Série de Laurent

Karl Weierstrass.

Cet article traite du développement en série de Laurent en analyse complexe. Pour la définition et les propriétés des séries de Laurent formelles en algèbre, veuillez consulter l'article Série de Laurent formelle.

En analyse complexe, la série de Laurent (aussi appelée développement de Laurent) d'une fonction holomorphe f est une manière de représenter f au voisinage d'une singularité, ou plus généralement, autour d'un "trou" de son domaine de définition. On représente f comme somme d'une série de puissances (positives et négatives) de la variable complexe.

Une fonction f d'une variable complexe est holomorphe si elle présente une régularité supérieure à la continuité. On peut directement supposer f développable en séries entières au voisinage de chaque point de son domaine de définition. Autrement dit, au voisinage d'un point a où f est définie, on peut écrire f(z) sous la forme :

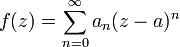$f(z)=\sum_{n=0}^{\infty}a_n(z-a)^n$ .

On a fait apparaitre une série entière en a, qui est la série de Taylor de f en a. Les séries de Laurent peuvent être vues comme une extension pour décrire f autour d'un point où elle n'est pas (a priori) définie. On inclut les puissances négatives ; une série de Laurent se présentera donc sous la forme:

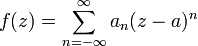$f(z)=\sum_{n=-\infty}^{\infty}a_n(z-a)^n$ .

Les séries de Laurent furent nommées ainsi après leur publication par Pierre Alphonse Laurent en 1843. Karl Weierstrass les découvrit le premier mais il ne publia pas sa découverte.

Le plus souvent, les auteurs d'analyse complexe présentent les séries de Laurent pour les fonctions holomorphes définies sur des couronnes, c'est-à-dire des ouverts du plan complexe délimitées par deux cercles concentriques. Mais elles permettent de mieux comprendre le comportement d'une fonction holomorphe autour d'une singularité.

Sommaire

1 Énoncé
- 1.1 Sur un exemple
2 Preuves
- 2.1 Par la théorie de Fourier
- 2.2 Par la formule intégrale de Cauchy

Énoncé

Une couronne centrée en a est un ouvert du plan complexe C délimité par au plus deux cercles de centre a. En général, une couronne est délimitée par deux cercles de rayons respectifs r < R. Plusieurs cas dégénérés peuvent toutefois être envisagés:

Si R vaut l'infini, la couronne considérée est le complémentaire du disque fermé de centre a et de rayon r ;
Si r vaut 0, la couronne correspond au disque ouvert de centre a et de rayon R, privé de a. On parle aussi dans ce cas de disque apointé ;
Si r vaut 0 et R l'infini, alors la couronne est le plan complexe privé du point a.

Pour toute fonction holomorphe f sur une couronne C centrée en a, il existe une unique suite 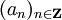$(a_n)_{n\in\mathbf{Z}}$ qui dépend seulement de f telle que:

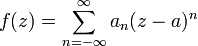$f(z)=\sum_{n=-\infty}^{\infty} a_n(z-a)^n$ ,

où la série de fonctions converge normalement sur tout compact de la couronne C. De plus, les coefficients a_n sont donnés par:

$a_n=\frac{1}{2\pi i} \oint_\gamma \frac{f(z)\,dz}{(z-a)^{n+1}}\, ,$

où $γ$ est le paramétrage d'un cercle de centre a tracé dans la couronne.

Sur un exemple

Une fonction rationnelle est holomorphe en dehors de ses pôles. On exprime la série de Laurent d'une fonction rationnelle F en un pôle a, en calculant la série de Taylor de (z-a)ⁿF(z) avec n suffisamment grand. Par exemple, on trouve la série de Laurent en j (racine troisième de l'unité):

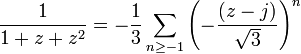$\frac{1}{1+z+z^2}=-\frac{1}{3}\sum_{n\geq -1} {\left(-\frac{(z-j)}{\sqrt{3}}\right)}^n$ .

En effet, j et j² sont les racines du polynôme 1+Z+Z². On est donc en mesure d'écrire, avec y = z - j:

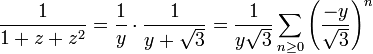$\frac{1}{1+z+z^2}=\frac{1}{y}\cdot\frac{1}{y+\sqrt{3}}=\frac{1}{y\sqrt{3}}\sum_{n\geq 0}{\left(\frac{-y}{\sqrt{3}}\right)}^n$ .

Ce genre de techniques se généralise en algèbre pour développer des fractions rationnelles en série de Laurent formelle (ou série méromorphe formelle). Ce type de développement peut en effet être adapté sur tout anneau.

Preuves

On propose deux preuves différentes de l'existence de la série de Laurent, et de son mode de convergence:

La première preuve s'appuie sur la théorie de Fourier, qui cherche à décomposer les fonctions d'une variable réelle périodiques en une somme de sinusoïdales ;
La seconde preuve s'appuie directement sur la formule intégrale de Cauchy, qui permet d'écrire la valeur d'une fonction holomorphe en un point comme une certaine intégrale curviligne sur un contour qui entoure le point.

Pour simplifier les notations, on suppose, sans perte de généralité, a = 0. On peut s'y ramener par l'action de la translation 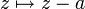$z\mapsto z-a$ . On suppose donc que f est une fonction holomorphe sur la couronne C délimitée par les deux cercles de centre 0 et de rayons respectifs r < R.

Par la théorie de Fourier

Joseph Fourier, dont la théorie porte le nom.

La restriction de f au cercle de rayon s (compris entre r et R) peut être regardée comme une fonction $2 p i$ -périodique d'une variable réelle f_s: il suffit d'exprimer f(z) en fonction de l'argument de z. On pose:

f s (t) = f (s e i t)

Le théorème de convergence de Dirichlet s'applique aux fonctions périodiques continues f_s et permet de les décomposer comme somme de sinusoïdales. Plus exactement, on peut faire apparaitre des coefficients de Fourier $c n (f, s)$ (qui dépendent du choix de s) tels que:

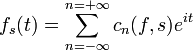$f_s(t)=\sum_{n=-\infty}^{n=+\infty} c_n(f,s)e^{i t}$ .

Or, comme la fonction f_s est de classe au moins C², la série de Fourier converge normalement vers f_s. Ce résultat général de la théorie de Fourier se démontre en utilisant des estimations sur la vitesse de convergence des coefficients de Fourier. En reprenant l'argument, on pourra obtenir la convergence normale sur tout compact de la série, vue comme série de fonctions en s et t. Fort malheureusement, la série obtenue n'est pas, du moins en apparence, exactement de la forme recherchée : des puissances de z doivent apparaître. Il est donc nécessaire de faire sortir la dépendance des coefficients de Fourier $c n (f, s)$ en le module s. Plus précisément, il faut chercher à définir des coefficients complexes $a n$ vérifiant:

c n (f, s) = a n (f) s n

. (*)

Or, on dispose d'une expression intégrale pour les coefficients de Fourier: par conséquent, $c n (f, s)$ en fonction de s peut être regardée comme une intégrale à paramètres. On peut chercher à établir sa régularité (au moins C¹ suffira amplement), puis à exprimer sa dérivée. Il est remarquable d'obtenir une équation différentielle relativement facile à intégrer:

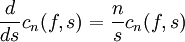$\frac{d}{ds}c_n(f,s)=\frac{n}{s}c_n(f,s)$ .

De cette équation différentielle découle effectivement (*), qui permet de voir f comme somme d'une série de Laurent qui converge au moins ponctuellement. Et la convergence normale sur tout compact de la couronne sera chose déjà obtenue. Toujours de (*) et de l'expression des coefficients de Fourier, on déduit:

$a_n(f)=\frac{c_n(f,s)}{s^n}=\oint_\gamma \frac{f(z)\,dz}{(z-c)^{n+1}}\, .$

Ainsi se démontre dans les grandes lignes l'existence de la série de Laurent en utilisant les seuls outils de la Théorie de Fourier.

Détails de la démonstration

Décomposition en séries de Fourier: Une fonction holomorphe est une fonction développable en séries entières en tout point de son domaine de définition. Par conséquent, elle est infiniment dérivable. Par composition, la fonction f_s définie ci-dessus est une fonction infiniment dérivable d'une variable réelle. Par ailleurs, elle est $2π$ -périodique. Le théorème de convergence de Dirichlet s'applique et montre que la fonction f_s est la somme de sa série de Fourier: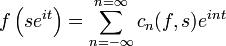; $f\left(se^{it}\right)=\sum_{n=-\infty}^{n=\infty}c_n(f,s)e^{int}$ .; où la série de fonctions converge au moins ponctuellement. Par ailleurs, on connait l'effet de la dérivation sur les coefficients de Fourier, décrit dans l'article Série de Fourier. Une intégration par parties fournit en effet: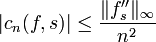; $|c_n(f,s)|\leq \frac{\|f_s''\|_{\infty}}{n^2}$ ,; où 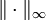$\|\cdot\|_{\infty}$ désigne la norme infini sur l'espace des fonctions bornées $2π$ -périodiques. Il est possible d'exprimer $f s''$ en fonction des premières dérivées de f. Fixons deux rayons intermédiaires r < u < U < R. La couronne fermée F délimitée par les cercles de rayon u et U est compacte (c'est en effet un fermé borné de C), et les dérivées de f sont des fonctions continues sur F, et donc bornées. Sans chercher à exprimer les dérivées de f au moyen de la formule intégrale de Cauchy, on obtient directement: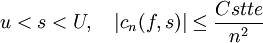; $u<s<U, \quad |c_n(f,s)|\leq \frac{Cstte}{n^2}$ .; Comme la série de terme général 1 / n² est sommable, la série de fonctions $\sum c_n(f,s)e^{int}$ est normalement convergente sur toute couronne fermée de C.
Convergence normale sur tout compact: Si K est un compact de C, l'application qui à un complexe associe son module induit une fonction continue sur K. Elle est donc bornée et atteint ses bornes. Autrement dit, on dispose d'un encadrement:; $\forall z\in K, \quad u\leq |z|\leq U$ ;; où les réels u et U se réalisent comme les modules d'éléments de K et a fortiori de C. Comme C est la couronne délimitée par les cercles de rayosn r et R, on en déduit r < u < U < R. Donc, K est inclus dans la couronne fermée délimitée par les cercles de rayons u et U, elle-même incluse dans C.; Comme tout compact de C esrt inclus dans une couronne fermée suffisamment grosse de C, la convergence normale sur toute couronne fermée de C (précédemment établie) implique la convergence normale sur tout compact de C.
Expression des coefficients de Fourier: Les coefficients de Fourier sont définis par la formule intégrale :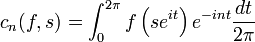; $c_n(f,s)=\int_0^{2\pi}f\left(se^{it}\right)e^{-int}\frac{dt}{2\pi}$ .; En particulier, $c n (f, s)$ est l'intégrale sur le segment [0, $2π$ ] d'une fonction continue dépendant d'un paramètre réel s. Cette fonction intégrée, comme fonction à deux variables, est continument différentiable. La dérivation sous le signe intégrale ne pose aucune difficulté. La fonction 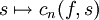$s\mapsto c_n(f,s)$ est définie et continument dérivable sur l'intervalle ouvert (r,R) et sa dérivée vaut:; $\frac{d}{ds}c_n(f,s)=\int_0^{2\pi}\frac{\partial}{\partial s}f\left(se^{it}\right)e^{-int}\frac{dt}{2\pi}$ .; Exprimons la dérivée partielle par rapport à s: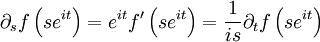; $\partial_s f\left(se^{it}\right)=e^{it}f'\left(se^{it}\right)=\frac{1}{is}\partial_tf\left(se^{it}\right)$ .; (En fait, on a établi les équations de Cauchy-Riemann en coordonnées polaires.) On injecte l'expression obtenue de la dérivée partielle par rapport s dans l'intégrale, puis on effectue (à nouveau) une intégration par parties: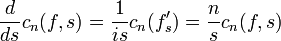; $\frac{d}{ds}c_n(f,s)=\frac{1}{is}c_n(f_s')=\frac{n}{s}c_n(f,s)$ .; Autrement dit, les coefficients de Fourier de $f s$ comme fonction de s vérifient une équation différentielle, à variables séparées, qu'il est donc facile d'intégrer. 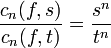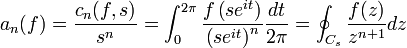Il vient, pour tout r < s, t < R:; $\frac{c_n(f,s)}{c_n(f,t)}=\frac{s^n}{t^n}$ .; En particulier, le rapport:; $a_n(f)=\frac{c_n(f,s)}{s^n}=\int_0^{2\pi}\frac{f\left(se^{it}\right)}{{\left(se^{it}\right)}^n}\frac{dt}{2\pi}= \oint_{C_s}\frac{f(z)}{z^{n+1}}dz$; est indépendant de s, et permet d'isoler la dépendance des coefficients de Fourier en s:; $c n (f, s) = a n (f) s n$ .
Conclusion: L'expression obtenue ci-dessus peut s'injecter dans la série de fonctions. Il vient :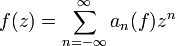; $f(z)=\sum_{n=-\infty}^{\infty} a_n(f)z^n$ .; On sait déjà que la série converge normalement sur tout compact de la couronnne C. L'unicité des coefficients a_nf découlent immédiatement de l'unicité des coefficients de Fourier. La démonstration est terminée.

Par la formule intégrale de Cauchy

Augustin Louis Cauchy.

La formule intégrale de Cauchy permet de représenter la valeur d'une fonction holomorphe f en z en fonction d'une expression intégrale le long d'une courbe fermée qui "entoure" z. C'est la formule intégrale de Cauchy qui permet d'obtenir le développement en séries entières de f au voisinage des points de son domaine de définition. Il est donc naturel de vouloir de nouveau exploiter cette formule ici pour obtenir le développement en séries de Laurent.

Le dessin ci-à droite décrit une courbe $γ$ tracée dans la couronne C, qui consiste à :

Parcourir une fois le cercle de centre 0 et de rayon S dans le sens trigonométrique ;
Aller de S à s en suivant le segment [s,S] ;
Parcourir le cercle de centre 0 et de rayon s dans le sens des aiguilles d'une montre ;
Retourner de s à S, toujours en suivant le segment [s,S].

Cette courbe $γ$ est contractile dans la couronne U et "renferme" la couronne ouverte C(s,S) délimitée par les cercles de rayons respectifs s < S. Si z est un nombre complexe (non réel positif) de module compris entre s et S, la formule intégrale de Cauchy s'applique donc en z et donne:

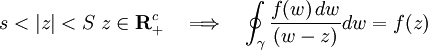$s<|z|<S \; z\in \mathbf{R}_+^c \quad\Longrightarrow\quad\oint_\gamma \frac{f(w)\,dw}{(w-z)}dw=f(z)$ .

Or, le lacet $γ$ a été décrit en concaténant des chemins, de sorte que l'intégrale curviligne se décompose en une somme de quatre intégrales curvilignes. On intègre deux fois le long du segment [s,S], la première fois de S à s, la seconde fois de s à S. Ces deux intégrales s'annulent. Par conséquent:

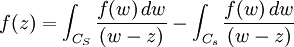
$f(z)=\int_{C_S} \frac{f(w)\, dw}{(w-z)} - \int_{C_s}\frac{f(w)\, dw}{(w-z)}$

où C_s et C_S désignent les cercles de rayons s et S. Cette formule reste valable pour tout nombre complexe w de module compris entre s et S.

Dans les deux intégrales, on peut exprimer l'intégrande comme une série de fonctions, qui font apparaitre des puissances de z, positives pour la première intégrale, négatives pour la seconde. L'inversion série-intégrale se justifie en évaluant la norme infinie des fonctions sommées. De la sorte, f(z) s'exprime comme la somme d'une série en puissances de z, de la forme:

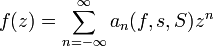$f(z)=\sum_{n=-\infty}^{\infty}a_n(f,s,S)z^n$ .

La convergence de la série est au moins ponctuelle. La même estimation sur les normes infini justifie la convergence normale de cette série sur tout compact contenu dans la couronne ouverte C(s,S). On aura donc écrit f comme somme d'une série de Laurent sur chaque couronne ouverte C(s,S) fortement incluse dans C. Pour obtenir l'indépendance des coefficients en s et S, il faut à nouveau effectuer une interversion série-intégrale. Le calcul fournit aussi l'unicité des coefficients, et l'expression annoncée.

Détails de la démonstration

Dans toute la première partie de la preuve, s et S sont deux rayons intermédiaires fixés: r < s S < R. Ils permettent de définir la couronne ouverte C(s,S) en restriction de laquelle on va travailler.

Application de la formule intégrale de Cauchy

Soit un nombre complexe z de module compris entre s et S. La droite Rz sectionne les cercles de rayons s et S en des points a et b de sorte que le segment [a,b] ne contienne pas z (voir figure). On introduit

γ w

le lacet obtenu:

En parcourant une fois le cercle de rayon S dans le sens trigonométrique ;
En suivant le segment [b,a] ;
En parcourant une fois le cercle de rayon s dans le sens des aiguilles d'une montre ;
Puis en suivant le segment [a,b].

En regardant les intersections du lacet

γ w

avec la droite Rw, on montre sans difficulté que l'indice de

γ z

en w vaut 1.

La formule intégrale de Cauchy s'applique et donne:

$f(z)=\oint_{\gamma_z} \frac{f(w)}{w-z}\, dw$ .

Compte-tenu des orientations sur les cercles, il vient:

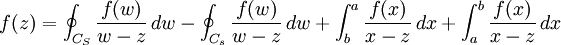$f(z)=\oint_{C_S}\frac{f(w)}{w-z}\, dw-\oint_{C_s}\frac{f(w)}{w-z}\, dw+\int_b^a\frac{f(x)}{x-z}\, dx+\int_a^b\frac{f(x)}{x-z}\, dx$ .

Après simplification:

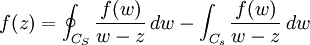$f(z)=\oint_{C_S}\frac{f(w)}{w-z}\,dw-\int_{C_s}\frac{f(w)}{w-z}\, dw$ .

Développement de la première intégrale

Comme le module de z est plus petit que S, on peut penser à développer l'intégrande en puissances de z / w:

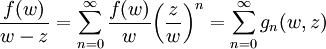$\frac{f(w)}{w-z}=\sum_{n=0}^{\infty} \frac{f(w)}{w}{\left(\frac{z}{w}\right)}^n=\sum_{n=0}^{\infty}g_n(w,z)$ ;

avec: 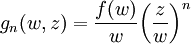$g_n(w,z)=\frac{f(w)}{w}{\left(\frac{z}{w}\right)}^n$ .

Majorons la fonction g_n. Pour tout w de module S, et si s < w < r.S (avec r < 1), on a:

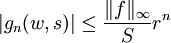
$|g_n(w,s)|\leq \frac{\|f\|_{\infty}}{S}r^n$

où 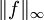$\|f\|_{\infty}$ désigne le supremum du module de f sur C(s,S). Comme la série géométrique converge, la série de terme général

g n (., w)

converge normalement sur le cercle de rayon S. Par conséquent, nous pouvons effectuer l'interversion série-intégrale:

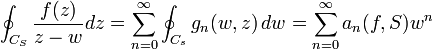$\oint_{C_S}\frac{f(z)}{z-w}dz=\sum_{n=0}^{\infty}\oint_{C_s}g_n(w,z)\, dw=\sum_{n=0}^{\infty}a_n(f,S)w^n$ ;

avec: 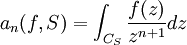$a_n(f,S)=\int_{C_S}\frac{f(z)}{z^{n+1}}dz$ .

La série de terme général

a n (f, S) w n

converge normalement sur la couronne ouverte délimitée par s et r.S avec r < 1.

Développement de la seconde intégrale

Pour la seconde intégrale, on développe l'intégrande par puissances de w / z:

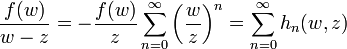$\frac{f(w)}{w-z}=-\frac{f(w)}{z}\sum_{n=0}^{\infty} {\left(\frac{w}{z}\right)}^n=\sum_{n=0}^{\infty}h_n(w,z)$ .

Pour w de module s, et z de module compris entre R.s et S (avec R > 1):

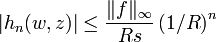$|h_n(w,z)|\leq \frac{\|f\|_{\infty}}{Rs}\left(1/R\right)^n$ .

Comme ci-dessus, cette majoration fournit la convergence normale sur le cercle de rayon s de la série de terme général

h n (., z)

. L'interversion série-intégrale s'en trouve justifiée:

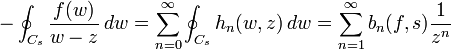$-\oint_{C_s}\frac{f(w)}{w-z}\, dw=\sum_{n=0}^{\infty}\oint_{C_s}h_n(w,z)\, dw=\sum_{n=1}^{\infty} b_n(f,s)\frac{1}{z^n}$ ;

avec: 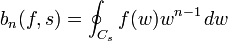$b_n(f,s)=\oint_{C_s}f(w)w^{n-1}\, dw$ .

La série converge normalement sur toute couronne délimitée par les cercles de rayons R.s et S, avec R > 1.

Convergence normale sur tout compact

En combinant les trois égalités précédentes, il vient, pour tout w dans C(s,S):

$f(z)=\sum_{n=0}^{\infty}a_n(f,S)z^n+\sum_{n=1}^{\infty}b_n(f,s){\left(1/z\right)}^n$ .

Tout compact K de la couronne ouverte C(s,S) est compris dans une couronne fermée délimitée par des rayons R.s et r.S, avec r < 1 < R. Le lecteur est prié de se reporter à la première preuve, où cet argument est détaillé. Or, les deux étapes précédentes ont démontré que les deux séries convergent normalement sur cette couronne fermée, a fortiori sur le compact K.

Sur la couronne C(s,S), la fonction f est donc la somme d'une série de Laurent qui converge normalement sur tout compact. Pour étendre cette décomposition à toute la couronne C, il suffit de montrer que les coefficients précédents sont indépendants de s et S.

Indépendance en s et S

Fixons un rayon intermédiaire s < T < S. Alors, les deux séries précédentes convergent normalement au voisinage du cercle de rayon T. La convergence normale justifie les interversions séries-intégrales:

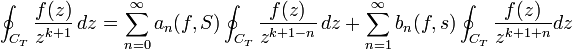$\oint_{C_T}\frac{f(z)}{z^{k+1}}\, dz=\sum_{n=0}^{\infty}a_n(f,S)\oint_{C_T}\frac{f(z)}{z^{k+1-n}}\, dz + \sum_{n=1}^{\infty} b_n(f,s)\oint_{C_T}\frac{f(z)}{z^{k+1+n}}dz$ .

Dans l'article intégrale curviligne, le lecteur trouvera le résultat suivant:

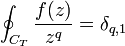$\oint_{C_T}\frac{f(z)}{z^q}=\delta_{q,1}$ .

Par conséquent :

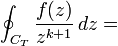
$\oint_{C_T}\frac{f(z)}{z^{k+1}}\, dz=$	$a n (f, S)$	si k = n ;
$\oint_{C_T}\frac{f(z)}{z^{k+1}}\, dz=$	$b n (f, s)$	si k = -n.

De fait, cette formule montre que les coefficient

a n (f, S)

b n (f, S)

ne dépendent pas de s et de S. Quand on fait varier s et S entre les limites r et R, il est en effet de fixer un rayon intermédiaire, du moins pour de petites variations. Par conséquent,

a n (f, S)

b n (f, S)

sont effectivement constants.

Portail des mathématiques

Ce document provient de « S%C3%A9rie de Laurent ».

Catégories : Analyse complexe | Série

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Série de laurent de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Serie de Laurent — Série de Laurent Karl Weierstrass. Cet article traite du développement en série de Laurent en analyse complexe. Pour la définition et les propriétés des séries de Laurent formelles en algèbre, veuillez consulter l article Série de Laurent… … Wikipédia en Français
Série de Laurent — Une fonction holomorphe dans une couronne de centre c s y développe en série de Laurent ; les coefficients de la série s expriment comme des intégrales sur un chemin fermé γ contenu dans la couronne et entourant c. Cet article traite du… … Wikipédia en Français
Serie de Laurent — En matemáticas, la serie de Laurent de una función compleja f(z) es la representación de la misma función en la forma de una serie de potencias, la cual también incluye términos de grado negativo. Esta serie se puede usar para expresar funciones… … Wikipedia Español
Serie formelle — Série formelle En mathématiques, les séries formelles sont un outil qui permet d utiliser l arsenal analytique des séries entières sans tenir compte de la notion de convergence. Pour cela on construit une série, non pas comme une fonction à l… … Wikipédia en Français
Serie de Taylor — sin(x) y aproximaciones de Taylor centradas en 0, con polinomios de grado 1, 3, 5, 7, 9, 11 y 13. En matemáticas, una serie de Taylor de una función f(x) infinitamente derivable (real o compleja) defin … Wikipedia Español
Laurent — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Pour les articles homophones, voir Loren, Lorent, Lauren, Laurant, Lorant et Loran (homonymie) … Wikipédia en Français
Série de Taylor — Pour les articles homonymes, voir Taylor. En mathématiques, et plus précisément en analyse, la série de Taylor d une fonction f (au voisinage d un point a) est une série entière construite à partir de f et de ses dérivées successives en a … Wikipédia en Français
Serie matemática — En matemáticas, una serie es la generalización de la suma a los términos de una sucesión. Informalmente, es el resultado de sumar los términos: a1 + a2 + a3 + · · lo cual suele escribirse en forma más… … Wikipedia Español
Laurent Lachance — en 2010 Laurent Lachance, M.A. (linguistique), B. Pédagogie, B.A. est un linguiste, pédagogue, auteur et créateur québécois. Né à Montréal le 16 mars 1931, Laurent Lachance fait ses études à l Université de Montréal où il obtient un… … Wikipédia en Français
Laurent Guénet — [[image … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Série de laurent

Série de Laurent

Sommaire