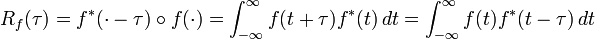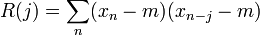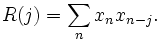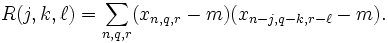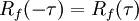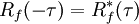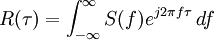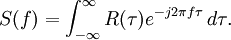Auto-corrélation

Autocorrélation

L'autocorrélation est un outil mathématique souvent utilisé en traitement du signal. C'est la corrélation croisée d'un signal par lui-même. L'autocorrélation permet de détecter des régularités, des profils répétés dans un signal comme un signal périodique perturbé par beaucoup de bruit, ou bien une fréquence fondamentale d'un signal qui ne contient pas effectivement cette fondamentale, mais l'implique avec plusieurs de ses harmoniques.

Définitions

Généralités

Note : La confusion est souvent faite entre l'autocovariance et l'autocorrélation obtenue en divisant cette dernière par la variance. Ces deux notions généralisent les notions classiques de covariance ayant pour dimension la dimension de la variable élevée au carré et de coefficient de corrélation compris entre -1 et +1. Les considérations qui suivent utilisent le langage le plus répandu chez les praticiens, sans division par la variance. Il existe d'autre part deux définitions fondamentalement différentes.

À un processus stochastique discret ou continu, correspond une « autocorrélation » statistique qui généralise la notion de covariance. Dans le cas d'un processus continu (en toute généralité complexe) 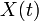$X(t)\,$ , la fonction d'autocorrélation statistique se définit comme :

$R_X(t1,t2) = E[X(t1).X^*(t2)]\,$

Dans le cas d'un signal stationnaire, on peut écrire :

$R_X(\tau) = E[X(t).X^*(t-\tau)]\,$

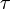$\tau\,$ est le décalage temporel et l'espérance mathématique se définit à partir de la densité de probabilité.

À partir d'un signal 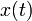$x(t)\,$ , on peut définir l'autocorrélation temporelle en remplaçant la moyenne d'ensemble par une moyenne temporelle (voir autocovariance) :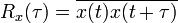

$R_x(\tau) = \overline{x(t) x(t+\tau)}$

Lorsque le signal est considéré comme réalisation d'un processus stationnaire ergodique, l'autocorrélation temporelle est identique à l'autocorrélation statistique. Elle peut être utilisée pour calculer le contenu en fréquence du signal (voir densité spectrale).

Dans certains problèmes, elle permet d'analyser le signal sans référence à son contenu en fréquences.

Statistiques

En statistique, l'autocorrélation d'une série temporelle discrète ou d'un processus X_t est simplement la corrélation du processus par rapport à une version décalée dans le temps de lui-même. Si X_t est un processus Stationnarité d'une série temporelle d'espérance μ alors la définition est

$R(k) = \frac{E[(X_i - \mu)(X_{i+k} - \mu)]}{\sigma^2}$

où E est l'espérance mathématique et k est le décalage temporel, $σ 2$ est la variance (statistiques et probabilités) et $μ$ la moyenne de la série. C'est une fonction à valeur dans l'intervalle [−1, 1] avec 1 indiquant une parfaite corrélation (Les signaux se recouvrent exactement quand le temps est décalé de k) et −1 indiquant une parfaite anti-corrélation. Il est d'usage pratique dans de nombreuses disciplines de tracer la normalisation par σ² et d'utiliser le terme autocorrélation sans distinction avec celui d'autocovariance.

Traitement du Signal

En traitement du signal, pour un signal donné f(t), l'autocorrélation continue R_f(τ) est la corrélation croisée continue de f(t) avec elle-même, à l'intervalle de temps τ, et est définie comme:

$R_f(\tau) = f^*(\cdot-\tau) \circ f(\cdot) = \int_{-\infty}^{\infty} f(t+\tau)f^*(t)\, dt = \int_{-\infty}^{\infty} f(t)f^*(t-\tau)\, dt$

où f^* représente le conjugué complexe et le cercle représente l'opération de convolution. Pour une fonction réelle, f^* = f.

Formellement, l'autocorrélation discrète R pour l'intervalle de temps j et le signal x_n est

$R(j) = \sum_n (x_n-m)(x_{n-j}-m) \,$

où m est la valeur moyenne (valeur attendue) de x_n. Souvent, les autocorrélations sont calculées pour un signal centré sur zéro. C’est-à-dire un signal dont la valeur moyenne est nulle. L'autocorrélation est alors définie par

$R(j) = \sum_n x_n x_{n-j}.\,$

L'autocorrélation multi-dimensionelle est définie de manière similaire. Par exemple, en trois dimensions l'autocorrélation devient

$R(j,k,\ell) = \sum_{n,q,r} (x_{n,q,r}-m)(x_{n-j,q-k,r-\ell}-m).$

Propriétés

Dans ce qui suit, nous décrirons les propriétés d'autocorrélation uni-dimensionnelle uniquement, puisque la plupart des propriétés sont facilement étendues du cas à une dimension aux cas multidimensionnels.

Une propriété fondamentale de l'autocorrélation est la symétrie, R(i) = R(−i), ce qui se démontre à partir de la définition. Dans un cas continu, l'autocorrélation est même une fonction paire

$R_f(-\tau) = R_f(\tau)\,$

quand f est une fonction réelle, et une fonction Hermitienne

$R_f(-\tau) = R_f^*(\tau)\,$

quand f est une fonction complexe.

La fonction continue d'autocorrélation atteint son pic à l'origine, où elle prend une valeur réelle. C’est-à-dire que pour tout délai τ, 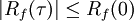$|R_f(\tau)| \leq R_f(0)$ . C'est une conséquence de l'inégalité de Cauchy-Schwarz. Le même résultat est obtenu pour un cas discret.

L'autocorrélation d'une fonction périodique est, elle-même, périodique avec exactement la même période.

L'autocorrélation de la somme de deux fonctions totalement non-corrélées (la corrélation croisée est zéro pour tout τ) est la somme des autocorrélations de chacune des fonctions.

Puisque l'autocorrélation est un type spécifique de corrélation croisée, elle conserve toutes les propriétés de la corrélation croisée.

L'autocorrélation d'un bruit blanc aura un pic important à τ = 0 et sera proche de 0 pour tout autre τ. Cela montre qu'un enregistrement de bruit blanc à un certain moment n'est pas corrélé statistiquement à un enregistrement du même bruit blanc à un autre moment.

Le théorème de Wiener–Khintchine rapporte la fonction d'autocorrélation à la densité spectrale de puissance par la transformée de Fourier:

$R(\tau) = \int_{-\infty}^\infty S(f) e^{j 2 \pi f \tau} \, df$

$S(f) = \int_{-\infty}^\infty R(\tau) e^{- j 2 \pi f \tau} \, d\tau.$

Applications

La mesure du spectre optique et la mesure de flash lumineux de très courte durée produit par laser, en utilisant un autocorrélateur optique.

En optique, l'autocorrélation normalisée et la corrélation croisée donnent le degré de cohérence d'un champ électromagnétique.

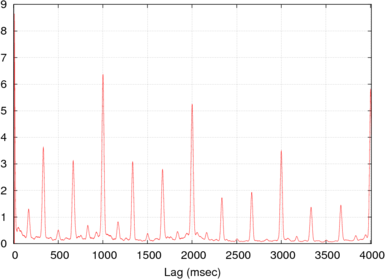
En traitement du signal, l'autocorrélation peut donner une information sur des événements répétés tels que les battements musicaux ou les fréquences de pulsar, même si cela ne peut pas donner la position dans le temps du battement.

L'exemple suivant montre le signal d'un fichier sonore MIDI Le Beau Danube bleu (à gauche), et son autocorrélation (seulement les 4 premières secondes).

Signal original, Le Beau Danube bleu.

L'autocorrélation du signal (les quatre premières secondes).

L'autocorrélation, utilisée précédemment comme intermédiaire dans le calcul d'une densité spectrale, est aujourd'hui abandonnée au profit de la transformation de Fourier rapide (voir aussi Analyse spectrale pour des considérations élémentaires).

Portail de la physique
Portail des probabilités et des statistiques

Ce document provient de « Autocorr%C3%A9lation ».

Catégories : Statistiques | Théorie du signal | Processus stochastique | Analyse harmonique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Auto-corrélation de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

fonction d'auto-corrélation — autokoreliacijos funkcija statusas T sritis automatika atitikmenys: angl. autocorrelation function vok. Autokorrelationsfunktion, f rus. автокорреляционная функция, f pranc. fonction d auto corrélation, f … Automatikos terminų žodynas
auto-féconder (s') — ⇒AUTO( )FÉCONDER (S ), (AUTOFÉCONDER , AUTO FÉCONDER ) verbe pronom. BOT. Se reproduire par autofécondation : • 1. Il convient d examiner séparément les espèces à fécondation obligatoirement croisée (presque tous les animaux) et celles qui s… … Encyclopédie Universelle
Correlation database — A Correlation database is a database management system (DBMS) that is data model independent and designed to efficiently handle unplanned, ad hoc queries in an analytical system environment. It was developed in 2005 by database architect Joseph… … Wikipedia
Auto-mutilation — Automutilation L’automutilation est le fait pour une personne de s infliger délibérément des blessures. Elle peut être faite dans plusieurs buts, comme se punir, ou pour se soulager de problèmes personnels ou professionnels. Sommaire 1 Définition … Wikipédia en Français
Auto-scarification — Automutilation L’automutilation est le fait pour une personne de s infliger délibérément des blessures. Elle peut être faite dans plusieurs buts, comme se punir, ou pour se soulager de problèmes personnels ou professionnels. Sommaire 1 Définition … Wikipédia en Français
Coefficient de corrélation multiple — Régression linéaire multiple Pour les articles homonymes, voir Régression. Sommaire 1 Modèle théorique 1.1 Exemple 1.2 E … Wikipédia en Français
Indice de Moran — En statistiques, l’indice de Moran (« Moran s I » est une mesure de l autocorrélation spatiale developpée par Patrick A.P. Moran[1]. L auto corrélation spatiale est caractérisée par une corrélation entre les mesures géographiquement… … Wikipédia en Français
Coefficient de détermination — Régression linéaire multiple Pour les articles homonymes, voir Régression. Sommaire 1 Modèle théorique 1.1 Exemple 1.2 E … Wikipédia en Français
Regression lineaire multiple — Régression linéaire multiple Pour les articles homonymes, voir Régression. Sommaire 1 Modèle théorique 1.1 Exemple 1.2 E … Wikipédia en Français
Régression linéaire multiple — Pour les articles homonymes, voir Régression. La régression linéaire multiple est une analyse statistique qui décrit les variations d une variable endogène associée aux variations de plusieurs variables exogènes. Par exemple, une analyse de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Auto-corrélation