Ruban de Möbius

Ruban de Möbius
Page d'aide sur l'homonymie Pour les articles homonymes, voir Moebius.
Réalisation à partir d'une bande de papier

En topologie, le ruban de Möbius (aussi appelé bande de Möbius ou anneau de Möbius) est une surface compacte dont le bord est homéomorphe à un cercle. Autrement dit, il ne possède qu'une seule face contrairement à un ruban classique qui en possède deux. Elle a la particularité d'être réglée et non-orientable. Cette surface a été décrite indépendamment en 1858 par les mathématiciens August Ferdinand Möbius (1790-1868) et Johann Benedict Listing (1808-1882). Le nom du premier fut retenu grâce à un mémoire présenté à l'Académie des sciences à Paris. On trouve également les dénominations de bande, anneau ou ceinture de Möbius, et on écrit parfois Moebius.

Il est facile de visualiser la bande de Möbius dans l'espace : un modèle simple se réalise en faisant subir une torsion d'un demi-tour à une longue bande de papier, puis en collant les deux extrémités.

Sommaire

Définition par torsion d'une bande dans l'espace

Plan de montage du ruban
Confection du ruban
Schématisation du montage : recoller les deux flèches en respectant le sens

Ruban de Möbius classique

Le ruban de Möbius peut être engendré par un segment pivotant dont le centre décrit un cercle fixe. Un paramétrage correspondant est

Ruban de Möbius
\begin{cases}x=(2+t \cos v ) \cos 2v \\y= (2+t \cos v ) \sin 2v \\ z=t \sin v \end{cases} \qquad \begin{matrix} -1\leq t\leq 1\\ 0 < v \leq \pi\end{matrix}

Les courbes v = v0, t variant seul, sont bien des segments, reliant à vitesse uniforme le point v = v0, t = - 1 et le point v = v0, t = 1. Ce segment est donc de longueur 2.

La courbe t = 0 est un cercle de rayon 2 dans le plan horizontal ; elle représente la trajectoire du centre des segments. L'angle que fait le segment avec la direction horizontale est v0. Lorsque le centre a fait un tour complet sur le cercle horizontal (ajout de π à la variable v), le segment a fait un demi-tour seulement. Ce qui provoque le raccordement par exemple du point t = 1, v = π avec t = - 1, v = 0.

Le bord du ruban est donné par la courbe t = 1 ou t = - 1. Mais c'est la même courbe : le bord du ruban de Möbius est en un seul morceau (connexe).

Ruban de Möbius animé

On peut également voir l'animation ci-dessus en vision stéréoscopique :

  • Animation stéréoscopique croisée : MobiusStereoCroisee.gif
  • Animation stéréoscopique parallèle du même ruban : MobiusStereoParallele.gif
  • Les deux animations regroupées sur une même animation : MobiusStereoGDG.gif

Autres figures obtenues par torsion

Des variantes du ruban classique peuvent s'obtenir en faisant subir à la bande de papier un nombre impair de demi-tours de sens direct ou rétrograde. Il suffit d'ajuster le paramétrage précédent :

Variante du ruban de Möbius
\begin{cases}x=(2+t \cos kv ) \cos 2v \\y= (2+t \cos kv ) \sin 2v \\ z=t \sin kv \end{cases} \qquad \begin{matrix} -1\leq t\leq 1\\ 0 < v \leq \pi\end{matrix}

avec k\, entier relatif impair.

Variante du Ruban de Möbius animé

Les figures obtenues pour k et -k sont énantiomorphes, c'est-à-dire des images miroirs l'une de l'autre.

Si l'on accepte des valeurs paires de k on obtient des rubans à deux faces, plus ou moins entortillés.

Comparaison des différents rubans

On peut s'intéresser à la courbe formant le bord de ces rubans. Elle a un entortillement différent pour chaque valeur de k. L'entortillement se calcule par exemple en projection (vue de dessus), en comptant le nombre de fois où la courbe passe au-dessus d'elle-même. On ne peut déformer continûment (c'est-à-dire par homotopie) un type de ruban en un autre dans l'espace de dimension 3.

Pourtant les différents rubans sont homéomorphes au ruban de Möbius classique, c’est-à-dire qu'il n'y a pas de différence intrinsèque entre eux. Celle-ci est liée à la façon dont ils sont plongés dans l'espace de dimension 3.

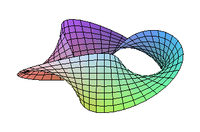
Le ruban de Möbius à un demi-tour peut également être vu comme une partie de la surface de Möbius.

Objets dérivés

Si on colle deux rubans de Möbius le long de leur bord, on obtient une bouteille de Klein.

Si on colle un disque à un ruban de Möbius le long de leur bord, on obtient une surface de Boy, c'est-à-dire une surface homéomorphe au plan projectif réel.

Si on tente de le découper en trois, c'est-à-dire en suivant un axe à un tiers de largeur d'un des bords, on obtient un ruban de Möbius d'un tiers de largeur et un ruban à deux faces d'un tiers de largeur, de longueur double et vrillé d'un tour complet.

Par extension, si on découpe un ruban de Möbius le long de son axe médian, on obtient un ruban à deux faces, vrillé et de longueur double. Si on recoupe ce ruban dans le sens de la longueur, on obtient deux anneaux distincts, vrillés et entortillés l'un sur l'autre.

Choix de longueur du ruban

Le ruban de Möbius peut se réaliser avec un ruban flexible de l'épaisseur d'une feuille de papier de 70 gr par exemple. Pour obtenir un ruban sans pliage brusque, il faut que, pour une largeur de ruban égale à 1, la longueur soit supérieure à 1,732 - soit la racine carrée de 3. Il est possible d'aller vers plus petit en longueur jusqu'à faire se rejoindre, avec un renversement hélicoïdal, les côtés opposés d'un carré, mais les pliages seront brusques.

Utilité du ruban

Bien que le ruban de Möbius puisse n'apparaître que comme une curiosité mathématique ou une construction artistique, cette disposition était souvent utilisée dans le monde industriel du XIXe siècle lorsque les machines fonctionnaient à partir de courroies. Les courroies étaient croisées à la jonction afin d'user les « deux côtés » de la courroie en même temps. En fait, la description du ruban de Möbius fera apparaître que la courroie n'avait qu'un seul côté.

Définition par identification abstraite

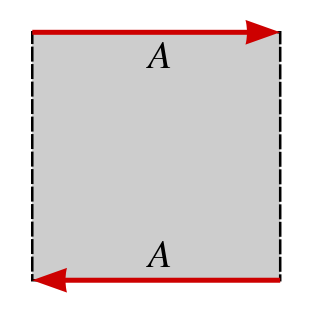
Mathématiquement, on peut définir le ruban comme l'ensemble quotient de l'ensemble \R \times [-1,1] \,\! par la relation d'équivalence définie par : (x,y) \sim (x',y') \,\! si et seulement si \exists k \in \Z \, ; \, (x',y') = (x+k,(-1)^k y) \,\!, muni de la topologie quotient. Par comparaison, un ruban « normal » (tronc de cylindre) serait défini par la relation \exists k \in \Z \, ; \, (x',y') = (x+k, y) \,\!.

Cela permet de voir mathématiquement ce qui se passe quand on découpe le ruban : si p:\R \times [-1,1] \rightarrow \R \times [-1,1]/\Z est l'application de passage au quotient, p(\R \times \{0\}) est un cercle dont le complémentaire est connexe.

On peut aussi réaliser le ruban de Möbius comme le complémentaire d'un disque ouvert dans le plan projectif réel (vu comme la sphère après identification des points diamétralement opposés).

Représentations artistiques

Le ruban de Möbius apparaît dans de très nombreuses productions artistiques.

Le ruban de Möbius est le logo universel des matériaux recyclables depuis 1970
  • Une version schématisée du ruban de Möbius est utilisée comme logo des matières recyclables depuis le premier Jour de la Terre en 1970. La boucle Möbius indique qu'un produit peut être recyclé, ou qu'il a été fabriqué à partir de matériaux recyclés[1]. Il s'agit en fait d'un ruban à trois demi-tours.
  • Une version du ruban de Möbius est utilisée comme logo pour Visual Studio, l'outil de développement informatique de Microsoft

Films et séries

  • Moebius, film de science fiction argentin de Gustavo Mosquera R., sorti en 1996.
  • Thru the Moebius Strip, film entièrement numérique de 80 minutes réalisé par Frank Foster à Global Digital Productions (Hong Kong)[2]. Le film est sorti aux Etats-Unis en 2005.
  • Le ruban de Möbius a aussi été utilisé dans le dessin d'une planète dans un épisode du dessin animé Ulysse 31.
  • Moebius est également le nom du double épisode final de la saison 8 de Stargate SG-1.
  • Lost Highway de David Lynch est souvent comparé à un ruban de Moebius. Au début de l'intrigue, Fred Madison, de l'intérieur de sa maison, reçoit un appel par interphone. Et à la fin, c'est lui-même, qui de l'extérieur de la maison, parle dans l'interphone, idem pour Timecrimes.

Cf. aussi Piège sur Zarkass de Stéfan Wul, roman dans lequel l'auteur base l'accès au sub-espace par le truchement de trois bandes de Moebius imbriquées ensemble.

Jeux vidéo

  • « Mobius 1 » est le nom de code (codename) du pilote contrôlé dans le jeu Ace Combat 4: Distant Thunder. Son insigne personnel est un ruban de Möbius.
  • « Mobius Ring » est une course des jeux F-Zero AX et F-Zero GX sortis en Arcade et sur Gamecube.
  • « Möbius maze » est l'un des huit lieux cachés dans le jeu de rôle Light of Oblivion sorti sur PlayStation et PC [réf. nécessaire].
  • « Möbius » était ce que beaucoup pensaient être le nom du monde de Sonic en Europe et aux États-Unis avant la sortie du jeu Sonic Adventure en 1999. Il s'agissait en réalité d'une erreur de traduction lors d'une interview de Yuji Naka (co-créateur de Sonic) qui parlait justement d'un motif du décor en spirale, qu'il qualifiait de « ruban de Möbius[3] ». L'erreur fut si bien reprise qu'on retrouvera le nom de Möbius désignant la planète où vit Sonic dans les comics d'Archie.
  • Dans S.T.A.L.K.E.R.: Clear Sky sur PC, le héros fait allusion au ruban de Möbius pour illustrer l'effet d'une « bulle anormale  » qui ramène inlassablement ceux qui y entrent à leur point de départ.
  • Dans StarCraft 2, on trouve la « Fondation Möbius », un mystérieux groupe à la recherche d'artefacts Protoss.
  • Dans la série Legacy of Kain, Moëbius est le gardien du temps

Romans

  • Dans 2010 : Odyssée deux, l'aberration de comportement de l'ordinateur HAL 9000 est désignée comme une « boucle de Hofstadter-Möbius ».
  • Dans Hyperion de Dan Simmons, le Cube de Möbius renferme l'énergie produite par les ergs.
  • Dans L'anneau de Moebius de Frank Thilliez, l'anneau est en réalité le schéma de l'histoire... (Il faut le lire pour comprendre.)
  • Dans Anges et démons, de Dan Brown, au paragraphe 31.
  • Dans la série Necroscope, de Brian Lumley, Harry Keogh, le héros, visualise fréquemment le ruban de Möbius afin d'ouvrir une porte pour naviguer dans l'espace-temps.

Sculptures et graphismes

  • Un énorme anneau de Möbius est représenté sous forme de sculpture à Lille, dans le quartier de Wazemmes. Cette sculpture, créée par Marco Slinckaert occupe le centre d'un rond-point en face de la CPAM. Elle est aussi appelée serpent par sa grande ressemblance. Une autre sculpture se situe à l'Université de Rennes 1, sur le campus de Beaulieu.
  • Max Bill a sculpté plusieurs rubans de Möbius, en particulier au Musée du Middelheim dans le parc du même nom à Antwerpen (Anvers) en Belgique. On peut également voir l'un de ses Endless Ring en granite au Centre Pompidou à Paris.
  • Keizo Ushio sculpte des rubans de Möbius découpés le long de leur ligne médiane. Voir par exemple [1].
  • Maurits Cornelis Escher, graveur et dessinateur néerlandais (1898-1972), a fait de nombreuses études sur le ruban de Möbius.
  • Pour les 20 ans du label Warp Records, une série d'images présentant des rubans de Möbius fut créée par Studio YES avec le photographe Dan Holdsworth. Certaines d'entre elles furent utilisées comme illustration pour des compilations.

La bande de Möbius chez Lacan

Dans le vocabulaire de Jacques Lacan : « 1962/63 - L'angoisse - 09/01/63 - Qu'est-ce qui fait qu'une image spéculaire est distincte de ce qu'elle représente ? c'est que la droite devient la gauche et inversement. - Une surface à une seule face ne peut pas être retournée. - Ainsi une bande de Mœbius, si vous en retournez une sur elle-même, elle sera toujours identique à elle-même. C'est ce que j'appelle n'avoir pas d'image spéculaire. »

Il convient de remarquer que, d'un point de vue mathématique, l'affirmation précédente de Lacan est erronée : on a vu dans les sections précédentes que l'image miroir d'un ruban de Möbius correspond à un retournement (avant collage) d'un demi-tour dans l'autre direction, et donc n'est pas identique au ruban initial.

Notes et références

Voir aussi

Articles connexes

et aussi

Liens externes

Mathématique
Pragmatique
Musique
Réflexions diverses

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Ruban de Möbius de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Ruban de Mobius — Ruban de Möbius Pour les articles homonymes, voir Moebius. Réalisation à partir d une bande de papier En topologie, le r …   Wikipédia en Français

  • Ruban de möbius — Pour les articles homonymes, voir Moebius. Réalisation à partir d une bande de papier En topologie, le r …   Wikipédia en Français

  • Ruban de Moebius — Ruban de Möbius Pour les articles homonymes, voir Moebius. Réalisation à partir d une bande de papier En topologie, le r …   Wikipédia en Français

  • Ruban de Moëbius — Ruban de Möbius Pour les articles homonymes, voir Moebius. Réalisation à partir d une bande de papier En topologie, le r …   Wikipédia en Français

  • ruban — [ rybɑ̃ ] n. m. • 1260; moy. néerl. ringhband « collier » 1 ♦ Étroite bande de tissu, servant d ornement, d attache. Ruban de coton, de velours, de soie. Ruban qui retient les cheveux. Nœud de rubans. ⇒ bouffette, chou, coque, rosette. Fleurs,… …   Encyclopédie Universelle

  • MÖBIUS (A. F.) — MÖBIUS AUGUST FERDINAND (1790 1868) Mathématicien et astronome allemand né à Schulpforta et mort à Leipzig. August Ferdinand Möbius fit ses études à Leipzig, à Göttingen (sous la direction de K. F. Gauss) et à Halle. En 1815, il devint professeur …   Encyclopédie Universelle

  • Möbius — (August Ferdinand) (1790 1868) mathématicien et astronome allemand. || GEOM Bande ou ruban de Möbius: surface qui ne possède qu une face, obtenue en tordant un ruban dont on joint les extrémités bout à bout …   Encyclopédie Universelle

  • Ruban — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Ruban », sur le Wiktionnaire (dictionnaire universel) Un ruban est une bande longue et étroite d un… …   Wikipédia en Français

  • Mobius — Moebius Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le nom Möbius (également orthographié Moebius, se prononce /mœ.bɪus/) peut désigner  …   Wikipédia en Français

  • Möbius — Moebius Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le nom Möbius (également orthographié Moebius, se prononce /mœ.bɪus/) peut désigner  …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”