Principe de Hamilton

Principe de Hamilton: Principe variationnel

Un principe variationnel est un principe physique issu d'un problème exprimé sous une forme variationnelle. Dans de nombreux cas, la résolution des équations de la mécanique peut se ramener à la recherche de géodésiques dans un espace général approprié. D'une part, nous savons que ces géodésiques sont les extrémales d'une certaine intégrale représentant la longueur de l'arc joignant les points fixes dans cet espace. Par conséquent, nous pouvons déjà prévoir qu'au moins dans certains cas, les problèmes de mécanique pourront s'exprimer comme des problèmes aux variations, autrement dit, en postulant que la variation première d'une certaine intégrale est nulle. On dira qu'on a réduit les problèmes à leur forme variationnelle. D'autre part, les équations d'Euler établies en mathématiques pour un problème aux variations sont semblables aux équations de Lagrange établies en physique pour résoudre des problèmes de mécanique ; cette similitude suggère bien évidemment aussi la possibilité de cette réduction à une forme variationnelle.

Sommaire

1 Principe de Fermat

2 Fonction de Hamilton ou Hamiltonien

3 Principe de Hamilton ou principe de moindre action de Lagrange

4 Principe de Maupertuis ou principe de moindre action

5 Principe de Gauss ou principe de moindre courbure

6 Comparaison entre mécanique rationnelle et optique géométrique

7 Équations d'Hamilton

8 Équation d'Hamilton-Jacobi

9 Systèmes conservatifs

10 Théorème de Liouville

11 Passage de la mécanique classique à la mécanique ondulatoire

12 Notes

13 Voir aussi

13.1 Bibliographie

13.2 Articles connexes

13.3 Liens externes

Principe de Fermat

Article détaillé : principe de Fermat.

Pierre de Fermat (1601–1665)

Bien qu'on puisse suivre la trace des principes variationnels d'une façon quasi continue de l'Antiquité à nos jours, il faut attendre plus d'un millénaire et demi — de Héron d'Alexandrie (vers la fin du I^er siècle ou le début du II^e siècle) au XVII^e siècle — jusqu'à Pierre de Fermat (1601–1665) pour en retrouver une application pratique. Le principe de Fermat, applicable aux rayons lumineux, peut s'écrire comme suit en tenant compte des perfectionnements intervenus depuis l'époque de Fermat lui-même :

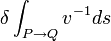
$\delta \int_{P \rightarrow Q} v^{-1} ds$

où P et Q sont deux points fixes, v désigne la vitesse de phase de la lumière et ds est l'élément d'arc du trajet emprunté par le rayon lumineux. La vitesse de phase de la lumière, autrement dit sa vitesse de propagation, peut varier avec le point considéré, mais non avec la direction du rayon en ce point.^[1] Cette équation exprime que la variation (indiquée par la lettre grecque $δ$ ) de l'intégrale curviligne 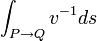$\int_{P \rightarrow Q} v^{-1} ds$ est nulle, c'est-à-dire que la différence entre cette intégrale évaluée le long de la trajectoire réelle et l'intégrale évaluée le long de n'importe quelle trajectoire virtuelle infiniment voisine est un infiniment petit du second ordre. Ceci ne signifie pas que l'intégrale est minimum, mais seulement qu'elle est extrémum. En effet, c'est seulement dans le cas où le trajet PQ est suffisamment petit, de manière à ce que des rayons « voisins » ne puissent recouper le rayon réel, que l'on peut démontrer qu'il s'agit effectivement d'un minimum.

Seulement la propriété que la première variation est nulle peut être étendue à un trajet PQ arbitraire, d'où le nom moderne de « principe variationnel » plutôt que celui, ancien, de « principe de minimum ». Et il faut bien reconnaître que cette modification de terme et d'interprétation fait perdre au principe de Fermat, sinon de son utilité, au moins un peu de la valeur esthétique et philosophique qui a indéniablement joué un rôle dans son élaboration.

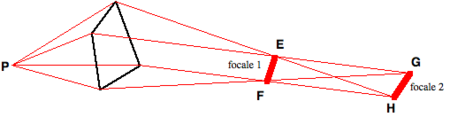
L'étude de certains systèmes optiques simples permet d'illustrer le problème. En effet, représentons le milieu hétérogène étudié par un de ces systèmes optiques. Dans cet exemple, l'image du point P, c'est-à-dire le lieu des points de rencontre de tous les rayons issus de P sous des angles légèrement différents, est constituée de deux focales EF et GH dont la distance caractérise l'astigmatisme du système. On peut alors montrer que l'intégrale curviligne 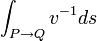$\int_{P \rightarrow Q} v^{-1} ds$ est minimale si le second point considéré, à savoir Q, tombe avant les deux focales, qu'elle est maximale si Q tombe après les deux focales, et qu'elle satisfait à une condition mixte (elle n'est ni un minimum, ni un maximum) si Q tombe entre les deux focales.

Fonction de Hamilton ou Hamiltonien

Article détaillé : mécanique hamiltonienne .

William Rowan Hamilton (1805–1865)

Le principe de Fermat est un principe variationnel particulièrement utile à l'optique géométrique. Pour résoudre des problèmes de mécanique, on utilise des principes variationnels faisant intervenir la fonction de Hamilton, que l'on désigne le plus souvent sous le terme de « Hamiltonien ». Pour arriver à comprendre le sens de cette fonction, considérons un problème à liaisons holonomes mais pouvant dépendre du temps t et qui admet le Lagrangien ^[2]

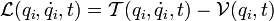
$\mathcal{L} ( q_i, \dot{q}_i, t ) = \mathcal{T} ( q_i, \dot{q}_i, t ) - \mathcal{V} (q_i, t)$

et étudions la valeur que prend l' intégrale d'action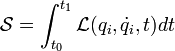

$\mathcal{S} = \int_{t_0}^{t_1 } \mathcal{L} ( q_i, \dot{q}_i, t ) dt$

au cours de l'évolution du système mécanique considéré.

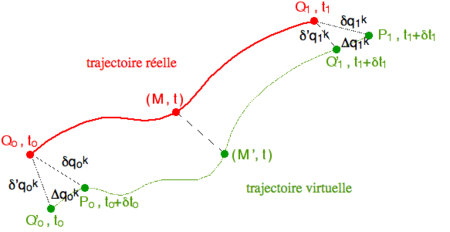
Supposons qu'au cours du mouvement naturel du système, le point représentatif dans l'espace de configuration parte d'une position initiale Q₀ à l'instant t₀ pour aboutir au point Q₁ à l'instant t₁. Cette trajectoire naturelle est représentée schématiquement sur la figure ci-contre par la courbe en rouge. Considérons un mouvement arbitraire partant de P_o voisin de Q_o à l'instant t_o + δt_o pour aboutir au point P₁ voisin de Q₁ à l'instant t₁ + δt₁.

Nous désirons comparer les valeurs de 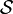$\mathcal{S}$ pour ces deux mouvements. Pour ce faire, nous calculons la variation de 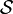$\mathcal{S}$ , c'est-à-dire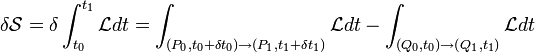

$\delta \mathcal{S} = \delta \int_{t_0}^{t_1} \mathcal{L} dt = \int_{ (P_0, t_0 + \delta t_0) \rightarrow( P_1, t_1 + \delta t_1)} \mathcal{L} dt - \int_{ (Q_0, t_0) \rightarrow( Q_1, t_1)} \mathcal{L} dt$

Au point M de coordonnées (q₁,q₂,...,q_f), atteint sur la trajectoire naturelle à l'instant t, nous associerons sur la trajectoire virtuelle arbitraire le point M' de coordonnées (q₁+δ'q₁,q₂+δ'q₂,...,q_f+δ'q_f) atteint également au même instant t. Soit Q'_o le point de la trajectoire variée, c'est–à-dire infiniment voisine de la trajectoire naturelle, atteint à l'instant t_o, et soit Q'₁ celui qui correspond à l'instant t₁. Notons les composantes de Q_oP_o, Q_oQ'_o, Q'_oP_o par δq_i,o, δ'q_i,o, Δq_i,o = (dq_i,o/dt) δt_o, respectivement, et celles de Q₁P₁, Q₁Q'₁, Q'₁P₁ par δq_i,1, δ'q_i,1, Δq_i,1 = q'_i,1 δt₁, respectivement.

La vitesse q'_i,1 sur la trajectoire variée ne diffère de celle sur la trajectoire réelle que par une quantité infiniment petite, laquelle ne donnerait dans Δq_i,1 qu'une correction du second ordre. En séparant les intégrations sur les segments terminaux Q'_oP_o et P₁Q'₁, nous obtenons :

$\delta \mathcal{S} = [ \mathcal{L}_1 \delta t_1 ]_{Q^{'}_1 P_1} - [ \mathcal{L}_0 \delta t_0 ]_{Q_0^{'} P_0} + \int_{ (Q_0^{'}, t_0) \rightarrow ( Q_1^{'}, t_1)} \mathcal{L} dt - \int_{ (Q_0, t_0) \rightarrow ( Q_1, t_1)} \mathcal{L} dt = [\mathcal{L}_1 \delta t_1]_{Q^{'}_1 P_1} - [ \mathcal{L}_0 \delta t_0 ]_{Q_0^{'} P_0} + \int_{ t_0 }^{t_1} \delta^{'} \mathcal{L} dt \;\;\;\;\; (1)$

L'intégrand δ'L dans la dernière intégrale est calculé entre des points des deux trajectoires correspondant aux mêmes instants t. On trouve que l'intégrale ∫_{t_o→t₁} δ'L dt vaut^[3]

$\int_{t_0}^{t_1} \delta^{'} \mathcal{L} dt = \sum_k \left[ \dfrac{ \partial \mathcal{L}}{\partial \dot{q}_k} \delta^{'} q_k \right]_1 - \sum_k \left[ \dfrac{ \partial \mathcal{L}}{\partial \dot{q}_k} \delta^{'} q_k \right]_0 + \int_{t_0}^{t_1} \sum_k \left[ \dfrac{ \partial \mathcal{L}}{\partial q_k} - \dfrac{d}{dt} \left( \dfrac{ \partial \mathcal{L}}{\partial \dot{q}_k}\right) \right] \delta^{'} q_k dt \;\;\;\;\; (2)$

En introduisant les moments conjugués p_k aux coordonnées généralisées contravariantes q_k, qui représentent les composantes covariantes de la vitesse, et en se souvenant que selon les équations de Lagrange,^[4] l'expression figurant entre crochets dans le dernier terme est nulle, on trouve finalement

$\delta \mathcal{S} = [ \mathcal{L}_1 \delta t_1 ]_{Q^{'}_1 P_1} - [ \mathcal{L}_0 \delta t_0 ]_{Q_0^{'} P_0} + \int_{ (Q_0^{'}, t_0) \rightarrow ( Q_1^{'}, t_1)} \mathcal{L} dt + \sum_k p_{k,1} \delta^{'} q_{k,1} - \sum_k p_{k,0} \delta^{'} q_{k,0} \;\;\;\;(3)$

Comme δ'q₁ = Q₁Q'₁ = Q₁P'₁ – Q'₁P'₁, il vient en termes de composantes : δ'q_k₁ = δq_k₁ – Δq_k₁ = δq_k₁ – q'_k₁ δt₁ et de même δ'q^k_o = δq_k_o – Δq_k_o = δq_k_o – q'_k_o δt_o. Dès lors, utilisant ces relations, on trouve sous forme condensée^[5]

$\delta \mathcal{S} = \left[ \sum_k p_k \delta q_k - \mathcal{H} \delta t \right]_0^1$

en définissant la fonction de Hamilton (ou le Hamiltonien)

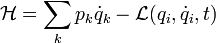
$\mathcal{H} = \sum_k p_k \dot{q}_k - \mathcal{L} ( q_i, \dot{q}_i, t )$

La fonction de Hamilton joue un rôle essentiel dans les principes généraux de la mécanique.

Principe de Hamilton ou principe de moindre action de Lagrange

Joseph-Louis Lagrange (1736–1813)

Seul un trajet dont la variation du lagrangien, au premier ordre, est nulle peut être utilisé par un corps.

Article détaillé : principe de moindre action.

Si nous admettons que toutes les trajectoires variées passent par les mêmes extrémités Q_o, Q₁ au même instant t_o, t₁ que la trajectoire réelle, la variation de l'intégrale d'action 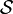$\mathcal{S}$ s'annule :

$\delta \mathcal{S} = \int_{t_0}^{t_1} \mathcal{L} dt = \int_{t_0}^{t_1} \sum_k \left[ \dfrac{ \partial \mathcal{L} }{ \partial q_k} - \dfrac{d}{dt}\left( \dfrac{\partial \mathcal{L}}{\partial \dot{q}_k} \right) \right] \delta^{'} q_k dt = 0$

d'après les équations de Lagrange. Inversement, si

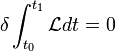
$\delta \int_{t_0}^{t_1} \mathcal{L} dt = 0$

il faut que les équations de Lagrange soient satisfaites, puisque les δ'q_k sont des quantités petites arbitraires. On peut encore en conclure que les équations d'Euler du problème aux variations sont identiques aux équations de Lagrange. Dès lors, le principe de Hamilton peut s'énoncer comme suit : Un système se meut d'une configuration à une autre de telle façon que la première variation de l'action

$\int_{t_0}^{t_1} \mathcal{L}( q_1, q_2, ..., q_f, \frac{dq_1}{dt}, \frac{dq_2}{dt}, ..., \frac{dq_f}{dt}, t) dt$

entre la trajectoire naturelle effectivement suivie et toute trajectoire virtuelle infiniment voisine ayant les mêmes extrémités dans l'espace et dans le temps soit nulle.

Ce principe possède une importance considérable qui dépasse l'équivalence formelle entre deux formulations mathématiques équivalentes du même problème. Ceci a d'ailleurs aussi son intérêt : par exemple, cette forme reste évidemment vraie dans n'importe quel système de coordonnées et, partant, on peut en déduire immédiatement l'invariance des équations de Lagrange pour toute transformation de coordonnées

$\dot{q}_i = \dot{q}_i (q_1, q_2, ..., q_f) \; \; \; \; avec \; \; i=1,2,...,f$

Mais surtout, ce principe ouvre la voie à une description de systèmes non-mécaniques par les méthodes mathématiques de la mécanique classique, comme dans la théorie des champs.

Principe de Maupertuis ou principe de moindre action

Pierre Louis de Maupertuis (1698–1759)

Le principe de moindre action de Maupertuis est la forme particulière que prend le principe de Hamilton pour les systèmes conservatifs à liaisons holonomes indépendantes du temps. Sous ces conditions, le potentiel s'écrit

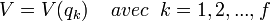
$V = V ( q_k ) \; \; \; \; avec \; \; k=1,2, ..., f$

et l'énergie cinétique devient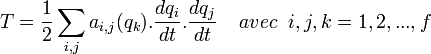

$T = \frac{1}{2} \sum_{i,j} a_{i,j} ( q_k ) . \dfrac{dq_i}{dt} . \dfrac{dq_j}{dt} \; \; \; \; avec \; \; i,j,k=1, 2, ..., f$

Dans ce cas, l'intégrale d'énergie prend la forme

$\mathcal{E} = T + V = constante$

et on en tire

$\mathcal{L} = T - V = 2T - \mathcal{E}$

ainsi que

$\mathcal{H} = \sum_k p_k \dfrac{dq_k}{dt} - \mathcal{L} = \sum_k \left[ \dfrac{ \partial T}{\partial \dot{q}_k} \right] \dfrac{dq_k}{dt} - \mathcal{L} = 2T - \mathcal{L} = T + V = \mathcal{E}$

Principe de Gauss ou principe de moindre courbure

Carl Friedrich Gauss (1777–1855)

Comparaison entre mécanique rationnelle et optique géométrique

On peut consulter à ce sujet l'analogie entre l'optique et la mécanique.

Équations d'Hamilton

Soit $\mathcal{H}$ la fonction de Hamilton du système, les équations canoniques de Hamilton s'écrivent alors: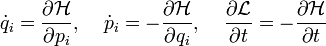

$\dot{q}_i = \dfrac{ \partial \mathcal{H} }{\partial p_i}, \;\;\;\; \dot{p}_i = - \dfrac{ \partial \mathcal{H} }{ \partial q_i } , \;\;\;\; \dfrac{\partial \mathcal{L} }{ \partial t } = - \dfrac{ \partial \mathcal{H} }{ \partial t }$

Démonstration

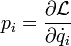Pour un système à g degrés de liberté, la fonction de Hamilton $\mathcal{H}$ est une fonction des coordonnées généralisées q_i du système, de ses moments généralisés p_i tel que $p_i = \dfrac{ \partial \mathcal{L} }{ \partial \dot{q}_i}$ et du temps t: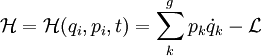

$\mathcal{H} = \mathcal{H} ( q_i, p_i, t ) = \sum_k^g p_k \dot{q}_k - \mathcal{L}$

$\mathcal{H}$ est la transformée de Legendre du lagrangien. Sa différentielle s'écrit:

$\begin{array}{ccl} d \mathcal{H} & = & \sum_{k=1}^g ( \dot{q}_k dp_k + p_k d\dot{q}_k ) - d\mathcal{L} \\ & = & \sum_{k=1}^g ( \dot{q}_k dp_k + p_k d\dot{q}_k - \dfrac{ \partial \mathcal{L} }{ \partial q_k} dq_k - \dfrac{ \partial \mathcal{L} }{ \partial \dot{q}_k} d\dot{q}_k - \dfrac{ \partial \mathcal{L} }{ \partial t} dt \\ & = & \sum_{k=1}^g ( \dot{q}_k dp_k - \dfrac{ \partial \mathcal{L} }{ \partial q_k} dq_k) - \dfrac{ \partial \mathcal{L} }{ \partial t} dt \\ & = & \sum_{k=1}^g ( \dot{q}_k dp_k - \dot{p}_k dq_k) - \dfrac{ \partial \mathcal{L} }{ \partial t} dt \\ & = & \sum_{k=1}^g ( \dfrac{ \partial \mathcal{H} }{ \partial p_k } dp_k + \dfrac{ \partial \mathcal{H} }{ \partial q_k } dq_k ) + \dfrac{ \partial \mathcal{H} }{ \partial t } dt \end{array}$

La dernière égalité permet de déduire les équations canoniques de Hamilton.

Équation d'Hamilton-Jacobi

L'équation d'Hamilton-Jacobi s'écrit:

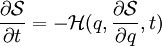
$\dfrac{ \partial \mathcal{S} }{ \partial t} = - \mathcal{H} ( q, \frac{ \partial \mathcal{S}}{\partial q}, t )$

Systèmes conservatifs

Théorème de Liouville

Article détaillé : Théorème de Liouville (Hamiltonien).

Joseph Liouville (1809–1882)

Passage de la mécanique classique à la mécanique ondulatoire

Notes

↑ Ceci est une restriction importante : on peut supposer que le milieu traversé par la lumière est hétérogène, mais il doit être optiquement isotrope. Le cas d'un milieu optiquement anisotrope, par exemple un cristal dont la symétrie n'est pas celle du système cubique, introduit une complication car il faut alors considérer un « rayon ordinaire » et un « rayon extraordinaire ».

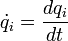
↑ avec $q i$ les coordonnées généralisées du système (i = 1, ..., g), g étant le nombre de degrés de liberté du système. On notera la dérivée par rapport au temps de la coordonnée généralisée $q i$ : $\dot{q}_i = \dfrac{dq_i}{dt}$

↑ Puisque M et M' sont des positions simultanées (correspondant à δ't = 0), la variation δ'L de la fonction de Lagrange L est δ'L = L(M') – L(M) = ∑_k [(∂L/∂q_k) δ'q_k + (∂L/∂q'_k) δ'q'_k)].
D'autre part, comme δ' et d/dt sont deux opérateurs qui peuvent commuter, on a aussi δ'q'_k = δ'(dq_k/dt) = d(δ'q_k)/dt, si bien que le dernier terme dans δ'L peut encore s'écrire (∂L/∂q'_k) δ'q_k = (∂L/∂q'_k) d(δ'q_k)/dt = d[(∂L/∂q'_k) δ'q_k]/dt – δ'q_k d(∂L/∂q'_k)/dt.
En introduisant cette expression dans le dernier terme de (1), on trouve (2).

↑ L'expression générale des équations de Lagrange en présence d'un Lagrangien L = L(q_k, q'_k, t) est d(∂L/∂q'_k)/dt – ∂L/∂q_k = 0.

↑ Avec ces relations, (3) devient δS = L₁ δt₁ + Σ_k p_k,1 (δq_k,1 – q'_k,1 δt₁) – [L_oδt_o + Σ_k p_k,o (δq_k,o– q'_k,o δt_o)] = (L₁ – Σ_k p_k,1 q'_k,1) δt₁ + Σ_k p_k,1 δq_k,1 – (L_o – Σ_k p_k,o q'_k,o) δt_o – Σ_k p_k,o δq_k,o ou δS = – H₁ δt₁ + Σ_k p_k,1 δq_k,1 + H_o δt_o – Σ_k p_k,o δq_k,o.

Voir aussi

Bibliographie

H. Goldstein (1980). Classical Mechanics (Second Edition), Addison-Wesley Publishing Company, Reading, Massachusetts. ISBN 0-201--02969-3.

Articles connexes

Calcul des variations

Principe variationnel en physique quantique

Liens externes

Portail des mathématiques

Portail de la physique

Portail de la géodésie et de la géophysique

Ce document provient de « Principe variationnel ».

Catégories : Mécanique | Optique | Physique théorique | Physique quantique | Géodésie | Principe physique

Contenu soumis à la licence CC-BY-SA. Source : Article Principe de Hamilton de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

Principe de moindre action de Lagrange — Principe variationnel Un principe variationnel est un principe physique issu d un problème exprimé sous une forme variationnelle. Dans de nombreux cas, la résolution des équations de la mécanique peut se ramener à la recherche de géodésiques dans … Wikipédia en Français
HAMILTON (W. R.) — Comme celle de beaucoup de ses contemporains, l’œuvre de Hamilton est remarquable par la diversité des thèmes scientifiques traités simultanément. Il fut l’objet de son vivant des plus grands honneurs, on l’appelait le «Lagrange irlandais», et… … Encyclopédie Universelle
Principe variationnel — Un principe variationnel est un principe physique issu d un problème exprimé sous une forme variationnelle. Dans de nombreux cas, la résolution des équations de la mécanique peut se ramener à la recherche de géodésiques dans un espace général… … Wikipédia en Français
Hamilton O. Smith — Hamilton Smith. Nacimiento 23 … Wikipedia Español
Principe du minimum de pontryagin — Le principe du minimum de Pontryagin est utilisé dans la théorie du contrôle optimal pour trouver la commande optimale permettant d amener un système dynamique d un état à un autre, en présence de contraintes portant sur l état ou les commandes d … Wikipédia en Français
Hamilton Fish — Mandats 26e Secrétaire d État des États Unis … Wikipédia en Français
Principe de moindre action — Joseph Louis Lagrange est le premier à définir mathématiquement le principe de moindre action. Le principe de moindre action est l hypothèse physique selon laquelle la dynamique d une quantité physique (la position, la vitesse et l accélération d … Wikipédia en Français
Hamilton (Ontario) — Para otros usos de este término, véase Hamilton. City of Hamilton Bandera … Wikipedia Español
Principe du minimum de Pontryagin — Le principe du minimum de Pontryagin est utilisé dans la théorie du contrôle optimal pour trouver la commande optimale permettant d amener un système dynamique d un état à un autre, en présence de contraintes portant sur l état ou les commandes d … Wikipédia en Français
principe variationnel d’Hamilton — Hamiltono variacinis principas statusas T sritis fizika atitikmenys: angl. Hamilton variation principle vok. Hamiltonsches Variationsprinzip, n rus. вариационный принцип Гамильтона, m pranc. principe variationnel d’Hamilton, m … Fizikos terminų žodynas

Mark and share
Search through all dictionaries
Translate…
Search Internet

Share the article and excerpts