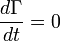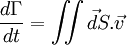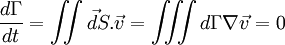- Theoreme de Liouville (Hamiltonien)
-
Théorème de Liouville (Hamiltonien)
 Pour les articles homonymes, voir Théorème de Liouville.
Pour les articles homonymes, voir Théorème de Liouville.En physique, le théorème de Liouville, nommé d'après le mathématicien Joseph Liouville, est un théorème utilisé par le formalisme hamiltonien de la mécanique classique, mais aussi en mécanique quantique et en physique statistique. Ce théorème dit que le volume de l'espace des phases est constant le long des trajectoires du système, autrement dit ce volume reste constant dans le temps.
Sommaire
Équation de Liouville
L'équation de Liouville décrit l'évolution temporelle de la densité de probabilité ρ dans l'espace des phases. Cette densité de probabilité est définie comme la probabilité pour que l'état du système soit représenté par un point à l'intérieur du volume Γ considéré.
En mécanique classique
On utilise les coordonnées généralisées (q,p)[1] où N est la dimension du système. La densité de probabilité est définie par la probabilité
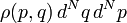 de rencontrer l'état[2] du système dans le volume infinitésimal
de rencontrer l'état[2] du système dans le volume infinitésimal 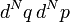 .
.Lorsqu'on calcule l'évolution temporelle cette densité de probabilité ρ(p,q), on obtient :
On utilise alors les équations canoniques de Hamilton, en les remplaçant dans l'équation précédente :
d'où :
en utilisant les crochets de Poisson.
DémonstrationOn considère l'équation de continuité d'un système conservatif :
or le second terme vaut[3] :
On obtient bien :
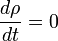
En mécanique quantique
D'après le principe de correspondance, on peut rapidement en déduire l'équation de Liouville en mécanique quantique :
d'où on déduit :
Ici,
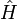 est l'opérateur hamiltonien et ρ la matrice densité. Parfois cette équation est aussi nommée l'équation de Von Neumann.
est l'opérateur hamiltonien et ρ la matrice densité. Parfois cette équation est aussi nommée l'équation de Von Neumann.Théorème de Liouville
De l'équation de Liouville, on peut prouver le théorème de Liouville, qui peut se formuler comme :
Théorème de Liouville — La fonction de distribution est constante le long de n'importe quelle trajectoire de l'espace des phases
ou bien :
Théorème de Liouville — Le volume d'une région de l'espace des phases reste constant lorqu'on suit cette région dans le temps
On peut montrer que le volume Γest constant :
Démonstrationoù
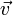 est le vecteur vitesse et
est le vecteur vitesse et 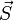 un vecteur surface de Γ
un vecteur surface de Γ
et à l'aide du théorème de Green-Ostrogradski, on trouvecar divergence du vecteur vitesse est nul[4].
Notes
- ↑ q = q1,...,qN et p = p1,...,pN.
- ↑ Un état est défini par l'ensemble des coordonnées généralisées qi et qi.
- ↑ d'après les équations canoniques de Hamilton.
- ↑ voir démonstration précédente
Voir aussi
Bibliographie
- C. Cohen-Tannoudji, B. Diu et F. Laloë, Mécanique quantique [détail des éditions]
- Albert Messiah, Mécanique quantique [détail des éditions]
- Portail de la physique
Catégories : Mécanique classique | Mécanique quantique | Physique statistique
Wikimedia Foundation. 2010.

![\frac{d \rho }{dt}=\frac{\partial \rho }{\partial t}+\sum_{i=1}^{N}\left[ \frac{\partial \rho }{\partial q_{i}}\dot{q}_{i}+\frac{\partial \rho }{\partial p_{i}}\dot{p}_{i}\right] = 0](/pictures/frwiki/102/f454ff658268ee5a08ef2c0c49c6a923.png)
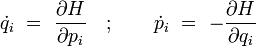
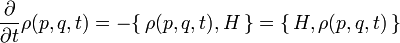
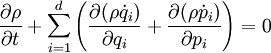
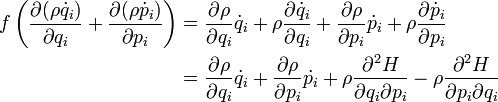
![\frac{1}{i\hbar} [\hat H,\hat A(t)] = \left\{ \hat H,\hat A \right\} + O(\hbar^2)](/pictures/frwiki/102/f91903673ad0d4fef3d0b824bc3a91c6.png)
![\frac{\partial}{\partial t}\hat \rho=\frac{i}{\hbar}[\hat\rho,\hat H]](/pictures/frwiki/53/5c89b1ce19809939cd2f2a3f5d991541.png)