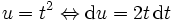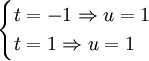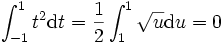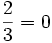- Preuve que 1 est égal à -1
-
Pseudo-démonstration d'égalité entre nombres
Le terme Pseudo-démonstration d'égalité renvoie à l'apparente exactitude de démonstrations d'égalités qui à l'évidence sont fausses. Étant donné que toute proposition fausse est équivalente à une autre proposition fausse, n'importe quel résultat faux est équivalent à
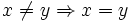 (un exemple célèbre est celui de Bertrand Russell avec l'égalité 2 + 2 = 5).
(un exemple célèbre est celui de Bertrand Russell avec l'égalité 2 + 2 = 5).Nous nous contenterons ici de regarder le cas d'égalités entre nombres, et nous détaillerons différents vices parmi les plus répandus qui conduisent à ces erreurs. Les méthodes proposées dans cet article se veulent en outre les méthodes les plus courantes, les plus instructives, et dans la mesure du possible, les plus directes.
Pseudo-démonstration via des identités remarquables et division par zéro
Principe
Cette pseudo-démonstration s'appuie sur l'erreur suivante :
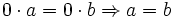
Elle s'effectue généralement en deux étapes :
- former via une identité remarquable un produit dans les deux membres d'une égalité dont l'un des facteurs est nul ;
- via une division par zéro obtenir un résultat absurde.
À noter que suivant l'identité remarquable utilisée et la manière dont on s'y prend, on peut obtenir n'importe quelle égalité fausse.
Le jeu consiste surtout à dissimuler la division par zéro dans des opérations très compliquées impliquant un grand nombre d'inconnues, ce qui rend difficile l'identification de la ligne fausse de la démonstration.
Cette technique est notamment utilisée pour « démontrer » que 1 + 1 = 3 dans L'Encyclopédie du savoir relatif et absolu de Bernard Werber.
Exemple
ExempleÉtape 1:
- Soit a et b deux réels non nuls, on pose
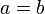
- On multiplie chaque membre par a
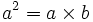
- On soustrait b2
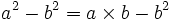
- On factorise chaque membre ( dans le premier on utilise une identité remarquable)
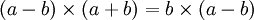
Étape 2:
- On divise par (a − b)
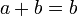
- Comme a = b, on remplace a par b
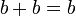
- Soit
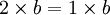
- On divise par b
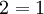
L'erreur est commise au moment ou l'on effectue la division par (a − b), car comme a = b alors a − b = 0 donc on divise par 0 ce qui est interdit.
Variante sans identité remarquable- On commence avec la proposition suivante :
2 = 1 + 1 - On multiplie chaque membre par (2 − 1) :
2(2 − 1) = (1 + 1)(2 − 1) - On développe :
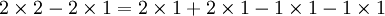
- On soustrait
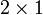 à chaque membre :
à chaque membre :
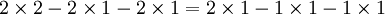
- On factorise :
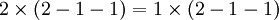
- On peut simplifier et on obtient :
2 = 1 - Il suffit d'ajouter 1 pour finalement avoir :
3 = 1 + 1
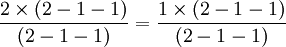
Pseudo-démonstration via des équations et confusion condition nécessaire et suffisante
Principe
Une autre pseudo-démonstration courante est de restreindre l'ensemble des solutions possibles d'une équation puis d'affirmer qu'un des éléments de l'ensemble est racine. Cela revient à faire l'erreur de logique suivante :
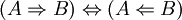 .
.Elle se déroule ainsi :
- étude de l'équation (restriction de l'ensemble des solutions possibles à un faible nombre, une ou deux) ;
- affirmation de l'ensemble des solutions possibles comme ensemble des solutions ;
- test de l'une des supposés racines et résultat absurde.
Exemple
ExempleÉtape 1 :
Considérons l'équation :
- x2 + x + 1 = 0
Ses solutions sont également celles (à l'exception de zéro) de :
Or d'après l'équation initiale :
Donc :
- x3 = − ( − x − 1) − x = 1
Étape 2 : La seule racine réelle possible est 1.
Étape 3 : En remplaçant x par 1 dans l'équation initiale, on obtient l'égalité 3 = 0.
Pseudo-démonstration via des racines carrées non définies
Principe
Il s'agit ici de l'erreur courante
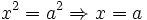 , l'implication correcte étant
, l'implication correcte étant 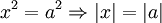 .
.Deux étapes :
- écrire une égalité vraie entre carrés ;
- appliquer l'implication fausse en écrivant l'égalité sans les carrés (en invoquant une fonction racine non définie, par exemple dans
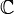 ).
).
On peut généraliser ce principe aux exponentielles complexes en invoquant une fonction logarithme non définie dans l'ensemble de travail, par exemple
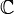 . Les racines carrées s'écrivent
. Les racines carrées s'écrivent 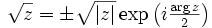 dans ce dernier ensemble.
dans ce dernier ensemble.Exemples
ExempleÉtape 1 :
Considérons l'égalité − 1 = − 1, qui peut s'écrire sous forme de quotients :
Or − 1 = i2 (voir nombre imaginaire), d'où
Étape 2 :
On prend la racine carrée des deux côtés ce qui donne :
En multipliant par i de part et d'autre, on obtient
- 1 = i2
Et puisque i2 = − 1, nous avons alors
- 1 = − 1
- ln( − 1) + ln( − 1) = ln(( − 1)2) = ln(1) = 0
Ainsi,
Et comme l'exponentielle est l'application réciproque du logarithme népérien :
- i = 1
Pseudo-démonstration via une sommation floue
Principe
En écrivant une somme de manière floue, c’est-à-dire non pas de manière formelle :
mais avec des points de suspensions :
la variable muette de sommation (notée ici k) est véritablement passée sous silence et le manque de formalisme des points de suspensions sert à masquer l'erreur.
Méthodologie :
- faire des calculs sur une somme ;
- générer une erreur via l'ensemble de définition de la variable muette, autrement dit le nombre de termes ;
- aboutissement à un résultat absurde.
Variantes
Variante via dérivationLa dérivation va s'effectuer différemment suivant le membre de l'égalité, à gauche il sera question d'une dérivation correcte, et à droite une dérivation sans tenir compte que la variable x est aussi le cardinal de l'ensemble des termes.
Étape 1 : Soit x un entier. Par définition de la fonction carrée :
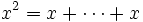 (x termes)
(x termes)
Étape 2 : En dérivant par rapport à x :
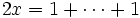 (x termes),
(x termes),
Étape 3 : d'où en simplifiant par x :
- 2 = 1
Variante via une suite arithmétiqueCette variante joue sur le nombre de termes de la somme des termes d'une suite arithmétique (ici la suite des n premiers entiers).
Étape 1 :
La somme des termes des n premiers entiers s'écrit :
Cela est vrai également au rang n − 1 :
D'où en ajoutant 1 dans chacun des membres :
Étape 2 :
Cette égalité peut aussi s'écrire :
D'après l'égalité au rang n, on a donc :
D'où :
Étape 3 :
Finalement :
L'erreur vient du fait que l'on compare les sommes
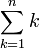 et
et 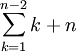 .
.Pseudo-démonstration via un changement de variable non licite lors d'une intégration
Principe
Lorsque l'on effectue un changement de variable lors d'une intégration sur un segment, il faut que le changement de variable soit un C1-difféomorphisme. Si le changement de variable est effectué trop hâtivement, il n'est pas rare de trouver un résultat absurde en fin d'intégration.
Démarche :
- calculer l'intégrale de manière correcte ;
- effectuer un changement de variable erroné ;
- confronter les deux résultats.
Exemple
ExempleÉtape 1 :
Considérons l'intégrale :
Par intégration en tant que monôme du second degré :
Étape 2 :
Effectuons le changement de variable de classe
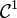 (mais qui n'est pas un
(mais qui n'est pas un 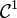 -difféomorphisme) :
-difféomorphisme) :Ainsi :
D'où :
Étape 3 :
Des deux calculs de l'intégrale on en déduit :
Voir aussi
- Portail des mathématiques
Catégorie : Raisonnement fallacieux
Wikimedia Foundation. 2010.

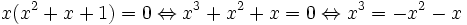
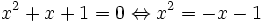
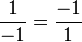
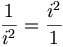
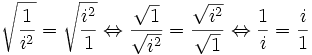
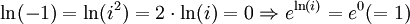
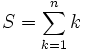
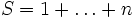
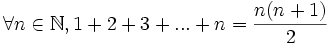
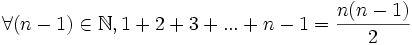
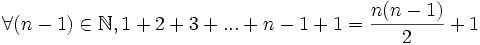
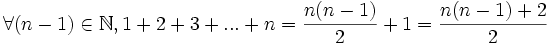
![\forall (n - 1) \in \mathbb{N}, \left[ \frac{n(n+1)}{2} = \frac{n(n-1) + 2}{2} \Leftrightarrow n(n+1) = n(n-1) + 2 \right]](/pictures/frwiki/102/f5176c9c07faee57c7b04c5d09a2a67e.png)
![\forall (n - 1) \in \mathbb{N}, \left[ n^2 + n = n^2 - n + 2 \Leftrightarrow 2n = 2 \right]](/pictures/frwiki/54/6a7da32ae9632342b85cf2e2e61ae932.png)
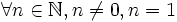
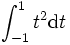
![\int_{-1}^1 t^2 {\rm d}t=\left[\frac{t^3}{3}\right]_{-1}^{1}=\frac{2}{3}](/pictures/frwiki/53/5550a80b7f059e0d0e21a231a0427120.png)