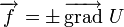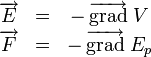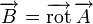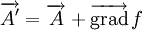Potentiel scalaire

Articles d'analyse vectorielle
Objets d'étude
Champ vectoriel	Champ scalaire
Équation aux dérivées partielles
de Laplace	de Poisson
Opérateurs
Nabla	Gradient
Rotationnel	Divergence
Laplacien scalaire	Bilaplacien
Laplacien vectoriel	D'alembertien
Théorèmes
de Green	de Stokes
de Helmholtz	de flux-divergence
du gradient	du rotationnel

En physique, le potentiel d'un champ vectoriel est une fonction scalaire ou vectorielle qui donne des représentations alternatives de champs vectoriels aux propriétés remarquables. Ainsi, un champ vectoriel irrotationnel peut être représenté par un potentiel scalaire tandis qu'un champ vectoriel dont la divergence est nulle peut être représenté par un potentiel vecteur. L'utilisation des potentiels permet bien souvent de simplifier les manipulations de ces champs vectoriels, et de là calculer plus facilement les grandeurs physiques associées.

Potentiel scalaire

Si le rotationnel d'un champ vectoriel est nul, alors on peut écrire ce champ vectoriel sous forme du gradient d'une fonction scalaire, c'est le potentiel scalaire (dans la pratique, on omet souvent l'adjectif). L'existence de ce potentiel scalaire est un résultat du théorème de Stokes. Plus précisément, en notant 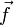le champ vectoriel et U le potentiel, on dit que le champ 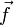dérive du potentiel U et on a

Pour un champ vectoriel donné, le potentiel scalaire n'est pas unique, il est défini à une constante près. D'autre part le signe est choisi par convention ou commodité.

On utilise des potentiels scalaires dans différentes situations.

• En mécanique, le champ gravitationnel dérive du potentiel gravitationnel.
• En électromagnétisme, le champ électrique dérive du potentiel électrique.
• En mécanique des fluides, le champ des vitesses d'un écoulement irrotationnel dérive d'un potentiel, on parle d'écoulement à potentiel des vitesses

Les deux premiers cas correspondent au cas particulièrement important des forces conservatives. La constante arbitraire est souvent choisie en fonction des conditions aux limites du problème, et on choisit le signe moins, de sorte qu'une position d'équilibre stable correspond à un minimum de l'énergie potentielle associée.

Dans ce contexte, on confond souvent potentiel et énergie potentielle. En prenant en exemple le cas du potentiel électrique, cette confusion vient du fait que la même relation relie le champ électrique 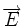et le potentiel V d'une part, la force 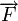et l'énergie potentielle E_p d'autre part :

On peut donc dire que la force dérive de l'énergie potentielle comme le champ dérive du potentiel, ou en d'autres termes que l'énergie potentielle est le potentiel scalaire associé à la force.

Notons toutefois que la seconde relation n'a un sens qu'à partir du moment où une particule chargée est placé dans le champ électrique. L'énergie potentielle E_p de la particule de charge q placée en un point et le potentiel V en ce point sont alors reliés par E_p = qV. La même relation relie la force et le champ électrique.

La situation est analogue pour le potentiel gravitationnel.

Potentiel vecteur

Si un champ vectoriel est de divergence nulle, alors on peut l'écrire comme le rotationnel d'un autre champ vectoriel, c'est le potentiel vecteur. Ce résultat nous est donné par le Théorème de Green-Ostrogradsky. En notant 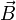le champ vectoriel et 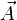le potentiel vecteur, on a :

De même que le potentiel scalaire, le potentiel vecteur n'est pas unique. En effet, le rotationnel d'un gradient étant toujours nul, on peut définir le potentiel vecteur à un gradient près. En d'autres termes, deux potentiels vecteurs reliés par une relation du type

représentent le même champ vectoriel.

Le potentiel vecteur le plus couramment utilisé est celui du champ magnétique en électromagnétisme. Il est également possible de définir un potentiel vecteur en mécanique des fluides dans le cas des écoulements de fluides incompressibles.

Voir aussi

• Potentiel vecteur du champ magnétique

• Portail de la physique