Ordre de grandeur (nombre)

Ordre de grandeur (nombres)

Cette liste compare les diverses tailles des nombres positifs, incluant le décompte des choses, les nombres sans dimension et les probabilités.

Plus petit que 10^-36

Informatique - Nombre à virgule flottante : 5x10^-324 est approximativement égal à la plus petite valeur positive différente de zéro qui peut être représentée par une valeur à virgule flottante IEEE à double précision.
Informatique - Nombre à virgule flottante : 1,4012985x10^-45 est approximativement égal à la plus petite valeur positive différente de zéro qui peut être représentée par une valeur à virgule flottante IEEE à simple précision.

10^-36

(0,000 000 000 000 000 000 000 000 000 000 000 001)

10^-33

(0,000 000 000 000 000 000 000 000 000 000 001)

10^-30

(0,000 000 000 000 000 000 000 000 000 001)

10^-27

(0,000 000 000 000 000 000 000 000 001)

10^-24

(0,000 000 000 000 000 000 000 001)

ISO : yocto - y

10^-21

(0,000 000 000 000 000 000 001, échelle courte: un sextillionnième, échelle longue : un trilliardième)

ISO : zepto - z

10^-18

(0,000 000 000 000 000 001, échelle courte : un quintillionnième, échelle longue : un trillionnième)

ISO : atto - a

10^-15

(0,000 000 000 000 001, échelle courte: un quadrillionnième, échelle longue : un billiardième)

ISO : femto - f

10^-12

(0,000 000 000 001, échelle courte : un trillionnième, échelle longue : un billionnième)

ISO : pico - p

mathématiques : Globalement, les chances d'obtenir face 40 fois de suite avec une pièce classique.

10^-9

(0.000 000 001; échelle courte : un billionnième; échelle longue : un milliardième)

ISO : nano - n

Loterie : Les chances de gagner le Grand prix (en ayant les 6 numéros) à la loterie US Powerball Multistate Lottery, avec un seul ticket, avec les règles de 2006, sont de 146 107 962 contre 1, pour une probabilité de 7 x 10^-9.
Loterie : Les chances de gagner le Jackpot (en ayant les 6 numéros principaux) à la loterie UK National Lottery, avec un seul ticket, avec les règles de 2003, sont de 13 983 816 contre 1, pour une probabilité de 7 x 10^-8.
Probabilités: la probabilité qu'un adulte de 20 à 60 ans pris au hasard meure dans l'heure qui suit est de l'ordre de 10^-8

10^-6

(0,000 001; échelle courte et échelle longue : un millionnième

ISO : micro - μ

Poker : Les chances d'obtenir une quinte flush royale (à l'as) servie en cinq cartes au poker avec un jeu de 52 cartes sont de 1,54 x 10^-6, soit 649 739 contre 1.

10^-5

(0,000 01; un cent millième)

Poker : La probabilité d'obtenir une quinte flush (autre qu'à l'as) au poker à 52 cartes est de 1,385 x 10^-5 (quand on admet les suites blanches) soit une chance à 72 192 contre 1.

10^-4

(0,000 1; un dix millième)

probabilité : Une vie humaine moyenne étant de trente mille jours, la probabilité qu'un être humain quelconque meure le lendemain, toutes choses égales par ailleurs, se situe quelque part entre 10^-4 et 10^-5.
Poker : Les chances d'obtenir un carré servi avec un jeu de 52 cartes au poker sont de 2,4 x 10^-4, soit à 4 164 contre 1.

10^-3

(0,001; un millième)

ISO: milli - m

Poker : Les chances d'obtenir un full au poker sont de 693 contre 1, pour une probabilité de 1,4 x 10^-3.
Poker : Les chances d'obtenir une couleur au poker sont de 508 contre 1, pour une probabilité de 1,9 x 10^-3.
Poker : Les chances d'obtenir une suite au poker sont de 254 contre 1, pour une probabilité de 4 x 10^-3
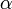$\alpha\,$ = 0,007 297 352 533(27), la constante de structure fine.

10^-2

(0,01; un centième)

ISO: centi - c

VIH : Environ 1,2 % de tous les humains de la tranche d'age 15-49 ans ont été infectés par le virus du SIDA à la fin de l'année 2001.
Poker : Les chances d'obtenir un brelan au poker sont de 46 contre 1, pour une probabilité de 0,021 (2,1 %)
Poker : Les chances d'obtenir deux paires au poker sont de 20 contre 1, pour une probabilité de 0,048 (4,8 %).

10^-1

(0,1; un dixième)

ISO: déci - d

Poker : Les chances d'obtenir seulement une paire au poker sont de 4 contre 3 (1,37 contre 1), pour une probabilité de 0,42 (42 %).
Poker : Les chances d'obtenir aucune paire au poker sont proche de 1 contre 2, pour une probabilité d'environ 0,5 (50 %)

10⁰

(1; un)

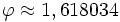$\varphi \approx 1,618034\,$ , c'est le nombre d'or.
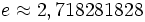$e \approx 2,718281828\,$ , la base des logarithmes naturels.
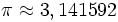$\pi \approx 3,141592\,$ , le rapport du diamètre d'un cercle avec sa circonférence.
7 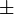$\pm\,$ 2, en sciences cognitives, l'estimation de George A. Miller du nombre d'objets qui peuvent être contenus simultanément dans la mémoire humaine.
Les huit planètes du système solaire, depuis 2006.

10¹

(10; dix)

ISO : deca - da

Il y a 10 doigts dans une paire de mains humaines.
Il y a 26 lettres dans l'alphabet latin.
Il y a 40 immortels à l'Académie française.

10²

(100; cent)

ISO : hecto - h

Dans les sports professionnels nord-américains, les joueurs portent typiquement des numéros d'uniformes allant de 1 à 99. Dans certains sports, 0 et 00 sont aussi permis, donnant 101 combinaisons différentes.
Il y a 128 caractères dans la table ASCII.
En 2006, il existe 192 états membres aux Nations unies.

10³

(1 000; mille)

ISO : kilo - k

Il y a 2 000-3 000 lettres dans une page de texte dactylographiée.
L'ADN des virus à ADN les plus simples possède environ 5 000 paires de bases.

10⁴

(10 000; dix mille)

10 000 : considéré dans la Grèce antique comme un très grand nombre. Les grecs l'appelaient murias, ce qui a donné en français, le mot myriade. C'est l'acte de naissance de la notion de grand nombre dans la civilisation occidentale.
Chaque neurone dans le cerveau humain est estimé être connecté à 10 000 autres.
Il existe 20 000 à 40 000 idéogrammes chinois, dépendant de la façon de les compter.
Chaque être humain est estimé avoir 30 000 à 40 000 gènes.
En juillet 2004, le plus grand nombre de décimales de 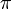$\pi\,$ π qui ont été récitées de mémoire - > 42 000.

10⁵

(100 000; cent mille)

Cheveux sur la tête : une chevelure humaine moyenne possède environ 100 000 à 150 000 cheveux.
Il y a 564 000 mots dans Guerre et paix.
Poker: on peut distribuer 201 376 mains différentes avec un jeu de 32 cartes.

10⁶

(1 000 000; échelle courte et échelle longue : un million)

ISO : mega (méga en français) - M

Espèces : Le World Resources Institute indique qu'approximativement 1,4 million d'espèces ont été nommées, en dehors d'un nombre inconnu d'espèces totales (intervalle estimé entre 2 et 100 millions d'espèces).
Échecs : Il existe 2 279 184 solutions pour le problème des n-reines pour n = 15.
Cartes à jouer : Il existe 2 598 960 mains de poker différentes de 5 cartes qui peuvent être distribuées à partir d'un jeu standard de 52 cartes.
Sites Web : en juillet 2003, le Netcraft web survey a estimé qu'il existait 42 millions de sites web distincts.
88 179 840 : le nombre de positions distinctes pour le Rubik's mini cube 2x2x2
Livres : La British Library indique qu'elle possède plus de 150 millions d'ouvrages. La Library of Congress indique qu'elle possède approximativement 119 millions d'ouvrage. Voir Gutenberg galaxy.
La base de données Freedb contient les informations (titres, artistes) d'environ 1 750 000 compact discs différents, en 2005.

10⁹

(1 000 000 000; échelle courte : 1 billion; échelle longue : 1 milliard)

ISO : giga - G

Étoiles cataloguées : Le Guide Star Catalog II possède des entrées pour 998 402 801 objets astronomiques distincts.
Limite calculatoire d'un CPU 32-bit : 2 147 483 647 est égal à 2³¹-1, et en tant que tel est le plus grand nombre qui peut être signé (complément à deux) en tant que nombre entier à 32-bit pour un ordinateur, et ainsi marque la limite supérieure calculatoire pour un CPU 32-bit.
1,5 à 3 milliards: nombre de secondes dans une vie humaine.
Paires de bases dans le génome : il y a approximativement 3 x 10⁹ paires de bases dans le génome humain.
1 065 000 000 - Population approximative de l'Inde en 2003.
1 300 000 000 - Population approximative de la République populaire de Chine en 2004.
6 378 000 000 - Population totale mondiale estimée en milieu d'année 2004.
Pages Web : il y a approximativement 8 x 10⁹ pages web indexées par Google en 2005.
Galaxies observables : il y a entre 1 x 10¹⁰ et 8 x 10¹⁰ galaxies dans l'univers observable (en 2003).
Neurones dans le cerveau : il y a approximativement 10¹¹ neurones dans le cerveau humain.
Étoiles dans notre galaxie : il y a approximativement 4 x 10¹¹ étoiles dans notre Galaxie.

10¹²

(1 000 000 000 000; échelle courte : 1 trillion; échelle longue : 1 billion)

ISO : téra - T

Chiffres connus de 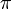$\pi\,$ : En 2002, le nombre de chiffres connus de 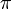$\pi\,$ était de 1 241 100 000 000.
Cellules dans le corps humain : le corps humain est constitué globalement de 10¹⁴ cellules

10¹⁵

(1 000 000 000 000 000; échelle courte : 1 quadrillion; échelle longue : 1 billiard)

ISO: Peta - P

Bactéries dans le corps humain : il y a globalement 10¹⁵ bactéries dans le corps humain.
Grains de sable : toutes les plages du monde mises ensemble font globalement 2 x 10¹⁵ grains de sable (Cette évaluation est totalement fantaisiste)

10¹⁸

(1 000 000 000 000 000 000; échelle courte : 1 quintillion; échelle longue : 1 trillion)

ISO: exa - E

Insectes : il a été estimé que la population des insectes sur Terre comprenait globalement 10¹⁸ insectes.
Rubik's Cube : il y a 4,3 x 10¹⁹ positions différentes d'un Rubik's Cube.

10²¹

(1 000 000 000 000 000 000 000; échelle courte : 1 sextillion; échelle longue : 1 trilliard)

ISO: zetta - Z

Étoiles dans l'univers observable : il a été estimé très approximativement à 7 x 10²² étoiles dans l'univers observable, basé sur le compte des galaxies et l'estimation des étoiles : (en anglais)
Il y a globalement 6,022 x 10²³ molécules dans une mole de n'importe quelle substance (nombre d'Avogadro).

10²⁴

(1 000 000 000 000 000 000 000 000; échelle courte : 1 septillion; échelle longue : 1 quadrillion)

ISO: yotta - Y

10²⁷

(1 000 000 000 000 000 000 000 000 000; échelle courte : 1 octillion; échelle longue : 1 quadrilliard)

Atomes dans le corps humain : le corps humain moyen contient globalement 7 x 10²⁷ atomes, voir (en anglais)

10³⁰

(1 000 000 000 000 000 000 000 000 000 000; échelle courte : 1 nonillion; échelle longue : 1 quintillion)

Mathématiques : La partition de 1 000 est égale à 24 061 467 864 032 622 473 692 149 727 991.

10³³

(1 000 000 000 000 000 000 000 000 000 000 000; échelle courte : 1 décillion; échelle longue : 1 quintilliard)

Mathématiques : 1 298 074 214 633 706 835 075 030 044 377 087 (≈ 1,3x10³⁴) est un nombre premier de Carol

10³⁶

(1 000 000 000 000 000 000 000 000 000 000 000 000; échelle courte : 1 undécillion; échelle longue : 1 sextillion)

Informatique - Intervalle d'adresses de l'IPv6 : (2¹²⁸) est approximativement égal à 3,410³⁸ et est le maximum théorique d'adresses internet qui peuvent être allouées avec le système d'adressage IPv6.
Informatique - Nombre à virgule flottante : 3,4028235x10³⁸ est approximativement égal à la plus grande valeur qui peut être représentée par une valeur à virgule flottante IEEE à simple précision.

10³⁹ à 10¹⁰⁰

Voir Nom des grands nombres pour les noms de ceux-ci et de nombres plus grands.

Mathématiques : 170 141 183 460 469 231 731 687 303 715 884 105 727 (≈1,7x10³⁹) est un nombre double de Mersenne premier.
Cosmologie : le nombre d'Eddington-Dirac est globalement égal à 10⁴⁰.
Physique : 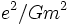$e^2/Gm^2 \,$ , le rapport électromagnétique des forces gravitationnelles entre deux protons, est globalement égal à 10⁴⁰.
Mathématiques : 53 694 226 297 143 959 644 031 344 050 777 763 036 004 353 (≈5.4x10⁴³ est un nombre premier de Pierpont
Mathématiques : 393 050 634 124 102 232 869 567 034 555 427 371 542 904 833 (≈3.910⁴⁴) est un nombre premier de Cullen
Géographie : il y a environ 10⁴⁷ molécules d'eau sur Terre
Géographie : la Terre est constituée globalement de 10⁵⁰ atomes
Mathématiques : 2,35x10⁵² : le nombre de positions distinctes pour le Rubik's Revenge 4x4x4.
Mathématiques : 359 334 085 968 622 831 041 960 188 598 043 661 065 388 726 959 079 837 (≈3,6x10⁵³ est un nombre de Bell premier.
Mathématiques : 808 017 424 794 512 875 886 459 904 961 710 757 005 754 368 000 000 000 est l'ordre du groupe Monstre
Cosmologie : 8x10⁶⁰ est globalement le nombre d'intervalles de temps de Planck puisque l'univers est reconnu comme étant créé par le Big Bang, il y a 13,7 ± 0.2 milliards d'années
Mathématiques : 709 601 635 082 267 320 966 424 084 955 776 789 770 864 725 643 996 885 415 676 682 297 (≈7x10⁶⁵ - Le plus grand nombre premier connu trouvé par la factorisation ECM en août 2005 [1]
Mathématiques - Cartes : 52! = 80 658 175 170 943 878 571 660 636 856 403 766 975 289 505 440 883 277 824 000 000 000 000 (≈8x10⁶⁷) = le nombre de manières d'ordonner les cartes d'un jeu de 52 cartes.
Mathématiques : 475 420 437 734 698 220 747 368 027 166 749 382 927 701 417 016 557 193 662 268 716 376 935 476 241 (≈4.8x10⁷¹) est un nombre de Fibonacci premier.
Astronomie : - particules fondamentales dans l'univers observable - Diverses sources estiment le nombre total de particules fondamentales dans l'univers observable dans l'intervalle 10⁸⁰; 10⁸⁵. Néanmoins, ces estimations sont vues comme des conjectures.
Mathématiques : 4,98x10⁸⁴ : le nombre de positions distinctes pour le Super Revenge ou Professor cube (5x5x5).
Mathématiques : 10¹⁰⁰, un gogol.

Plus grand que 10¹⁰⁰

10^{7 235 733}, l'ordre de grandeur du plus grand nombre premier connu, en janvier 2005. La valeur exacte de ce nombre premier record est 2^{24 036 583} - 1. Prouver la primalité des nombres avec un millier à plusieurs dizaines de milliers de chiffres, dépendant d'une forme spéciale, peut être faite en quelques minutes sur les ordinateurs modernes.
10^{80 000 000 000 000 000}, le plus grand nombre nommé dans Le compteur de sable du système d'Archimède.
10^gogol ( 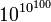$10^{10^{100}}$ ), un gogolplex
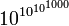$10^{\,\!10^{10^{1000}}}$ , ordre de grandeur d'une borne supérieure dans une démonstration de Skewes.

Note : Pour interpréter correctement les dernières entrées, garder à l'esprit que l'exponentiation est exécutée de droite à gauche. Par exemple,

$10^{\,\!10^{100}} \mbox{ veut dire } 10^{\,\!(10^{100})}$

Voir aussi

Liens externes

L'article de Seth Lloyd Computational capacity of the universe fournit un nombre de quantités sans dimension intéressantes (en anglais)

Ordres de grandeur
Densité · Données · Énergie · Fréquence · Longueur · Masse · Monétaire · Nombres · Pression · Puissance · Superficie · Température · Temps · Vitesse · Volume

Ce document provient de « Ordre de grandeur (nombres) ».

Catégorie : Nombre

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Ordre de grandeur (nombre) de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Ordre de grandeur — Un ordre de grandeur permet une représentation simplifiée et synthétique d une grandeur physique. Cette notion est utilisée pour communiquer sur des grandeurs de l infiniment grand ou de l infiniment petit. Scientifiquement, un ordre de grandeur… … Wikipédia en Français
Ordre de grandeur (donnees) — Ordre de grandeur (données) Cette liste compare les ordres de grandeur pour les données (ou l information), mesurée en bits. Cette article suppose une attitude formelle par rapport à la terminologie. Ce qui signifie deux choses : Un groupe… … Wikipédia en Français
Ordre de grandeur (donnée) — Ordre de grandeur (données) Cette liste compare les ordres de grandeur pour les données (ou l information), mesurée en bits. Cette article suppose une attitude formelle par rapport à la terminologie. Ce qui signifie deux choses : Un groupe… … Wikipédia en Français
Ordre de grandeur (nombres) — Cette liste compare les diverses tailles des nombres positifs. Elle inclut le décompte de choses, des nombres sans dimension et des probabilités. Sommaire Plus petit que 10 36 10 36 10 33 10 30 10 27 10 24 10 21 10 18 10 15 10 12 10 9 10 6 10 5 … Wikipédia en Français
Ordre de grandeur (données) — Cette liste compare les ordres de grandeur pour les données (ou l information), mesurée en bits. Cet article suppose une attitude formelle par rapport à la terminologie. Ce qui signifie deux choses : un groupe de 8 bits dans un ordinateur… … Wikipédia en Français
Ordre de grandeur (densité surfacique) — Ordres de grandeur de densité surfacique Facteur (m 2) Valeur (m 2) Exemple 10 6 1,3 x 10 6 Densité humaine sur toute la surface de la planète terre[1] 10 4 1,12 x 10 4 Nombre d habitant au mètre carré en France … Wikipédia en Français
Ordre de grandeur (temps) — Cet article présente une comparaison des ordres de grandeur de temps. Sommaire 1 Secondes 2 Années 3 Voir aussi 4 Références … Wikipédia en Français
ordre — [ ɔrdr ] n. m. • 1080 sens II; lat. ordo, ordinis I ♦ (1155) Relation intelligible entre une pluralité de termes. ⇒ organisation, structure; économie. « L idée de la forme se confond avec l idée de l ordre » (A. Cournot). 1 ♦ Didact. Disposition … Encyclopédie Universelle
nombre — [ nɔ̃br ] n. m. • déb. XIIe; lat. numerus I ♦ 1 ♦ Concept de base des mathématiques, une des notions fondamentales de l entendement que l on peut rapporter à d autres idées (de pluralité, d ensemble, de correspondance), mais non définir.… … Encyclopédie Universelle
grandeur — [ grɑ̃dɶr ] n. f. • mil. XIIe; de grand I ♦ (Sens absolu) 1 ♦ Vx Caractère de ce qui est de grande taille, de grande dimension. ♢ Mod. Loc. Regarder qqn du haut de sa grandeur, de haut en bas, avec un air de supériorité, de dédain. 2 ♦ (XIIe) … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Ordre de grandeur (nombre)