Nom Des Grands Nombres

Nom Des Grands Nombres

Nom des grands nombres

Les noms des grands nombres (supérieurs au trillion) ne sont pratiquement jamais utilisés, du moins dans un contexte de communication normale. De nombreux systèmes ont été proposés pour nommer des grands nombres, mais aucun ne semble avoir eu d'utilité pratique.

Sommaire

Usage des grands nombres

Quelques grands nombres ont réellement un sens pour l'homme, et sont d'un usage relativement courant jusqu'au trillion. Au delà, les noms de grands nombres n'ont plus guère qu'une existence artificielle, dans les définitions mathématiques, et il n'y pas d'occurrence de ces mots dans le langage courant.

Dans l'usage courant, ces grands nombres sont exprimés avec la notation scientifique. Avec cette notation, qui existe depuis les années 1800, les grands nombres sont exprimés par un dix et un nombre en exposant. On dira par exemple : « L'émission en rayons X de cette radio-galaxie est de 1,3·1045 erg ». Le nombre 1045 se lit simplement « dix puissance quarante-cinq » : c'est facile à lire, facile à comprendre, et beaucoup plus parlant que « quattuordécillion » (qui présente de plus l'inconvénient de signifier deux choses différentes, suivant que la convention utilisée est l'échelle longue ou courte).

Quand c'est une quantité physique qui doit être désignée, ce sont les préfixes du système international qui sont préférentiellement utilisés. Tout le monde comprendra ce qu'est une « femtoseconde », alors qu'un « billiardième de seconde » sera difficile à comprendre.

Ce n'est donc pas pour leur utilité pratique que les grands nombres sont nommés, mais ils ont de tous temps fasciné ceux qui se sont penchés sur eux en essayant d'appréhender ce que « grand nombre » pouvait bien signifier.

Système d'Archimède

Un des premiers exemples connus est le décompte que fit Archimède du nombre de grains de sable que pouvait contenir l'univers, dans l'Arénaire (Ψάμμιτης). Pour cela, il généralisa le système de numération grec, dont le terme le plus élevé s'appelait la myriade (104), ce qui permettait donc aux grecs de compter jusqu'à 99 999 999 (soit 108-1, la myriade de myriade n'ayant pas de nom).

Archimède appela ces nombres nommables en grec des « nombres de premier ordre » ; et appela la myriade de myriade, soit 108, l'unité de base des « nombres de deuxième ordre ». En prenant ce nombre comme nouvelle unité, Archimèdes était capable de nommer 99 999 999 nombres « de deuxième ordre », jusqu'à 108·108=1016. Ce nombre est à son tour pris comme l'unité des « nombres de troisième ordre », et ainsi de suite.

Archimède continua sa construction logique pour tous les « ordres » qui pouvaient être nommés en grec, c’est-à-dire jusqu'au nombre d'ordre une myriade de myriade, soit 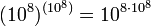(10^8)^{(10^8)}=10^{8\cdot 10^8}, fin naturelle de cette série de désignation.

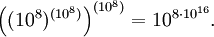
Archimède prolongea cette construction en prenant à nouveau ce nombre comme unité de base, ce qui lui permit d'étendre le système de dénomination jusqu'à \left((10^8)^{(10^8)}\right)^{(10^8)}=10^{8\cdot 10^{16}}.

À ce point, Archimède se servit de ce système de désignation pour estimer le nombre de grains de sable que pouvait contenir l'univers, parce que « innombrable comme les grains de sable » représentait pour les grecs l'exemple archétypal de quelque chose qui ne pouvait pas être compté. Il trouva comme ordre de grandeur « mille myriades du huitième ordre » (soit 1063).

Famille des -llions

Système de Nicolas Chuquet

Chuquet.gif

Nicolas Chuquet écrivit un livre, Triparty en la science des nombres, où l'on trouve le premier exposé de l'usage moderne de grouper les grands nombres par paquets de six chiffres, qu'il séparait par des points (on remarquera que les noms employés par Chuquet ne sont pas tout à fait les noms modernes).

Ou qui veut le premier point peult signiffier million Le second point byllion Le tiers poit tryllion Le quart quadrillion Le cinqe quyllion Le sixe sixlion Le sept.e septyllion Le huyte ottyllion Le neufe nonyllion et ainsi des ault's se plus oultre on vouloit preceder. Item lon doit savoir que ung million vault mille milliers de unitez, et ung byllion vault mille milliers de millions, et [ung] tryllion vault mille milliers de byllions, et ung quadrillion vault mille milliers de tryllions et ainsi des aultres : Et de ce en est pose ung exemple nombre divise et punctoye ainsi que devant est dit, tout lequel nombre monte 7 quadrillions 453248 tryllions 043000 byllions 700023 millions 654321. Exemple : 7'453248'043000'700023'654321.

Cependant, l'ouvrage de Chuquet ne fut pas publié de son vivant. Une bonne partie en fut copiée par Estienne de La Roche dans un ouvrage qu'il publia en 1520, L'arismetique.

Cette description est celle qui correspond au système dit de l'échelle longue, où les préfixes correspondent aux puissances du million. Le bymillion de Adam (byllion pour Chuquet) correspond donc à 1012, et le trimillion / tryllion vaut 1018.

C'est à Chuquet que l'on attribue l'invention du système, mais les premiers termes existaient avant lui. Les mots bymillion et trimillion apparaissent en 1475 dans un manuscrit de en:Jehan Adam.

  • Le terme Million existait avant Adam et Chuquet. C'est un mot d'origine probablement italienne, millione, forme intensifiée du mot mille: un million est étymologiquement un gros millier, rappelant les unités de second ordre d'Archimèdes.
  • La manière dont Adam et Chuquet présentent ces termes suggère qu'ils décrivent un usage préexistant, plutôt qu'une invention personnelle. Il est probable que des termes comme billion et trillion étaient déjà connus à cette époque, mais que Chuquet (expert dans l'art de manier les exposants) en a généralisé le système, inventant les noms correspondants aux puissances plus élevées.

Chuquet ne précisa que les dix premiers préfixes; l'extension de son système aux nombres supérieurs a toujours provoqué des variantes dans les solutions retenues pour adapter les noms latins au suffixe -llion.

Formation des noms en -llion

Le système de Nicolas Chuquet consiste à faire suivre les préfixes bi-, tri-,... du suffixe -llion, pour former les noms d'unité successifs. Dans le système original, qui correspond à l'échelle longue, chaque unité vaut 106 fois l'unité précédente. On a donc, de manière régulière :

Rang Désignation Valeur Déduction
1 mi-llion 106 =  1 000 000 1
2 bi-llion 1012 =  1 000 000 2
3 tri-llion 1018 =  1 000 000 3
4 quadri-llion 1024 =  1 000 000 4
5 quinti-llion 1030 =  1 000 000 5
6 sexti-llion 1036 =  1 000 000 6
7 septi-llion 1042 =  1 000 000 7
8 octi-llion 1048 =  1 000 000 8
9 noni-llion 1054 =  1 000 000 9
10 deci-llion 1060 =  1 000 00010  

Ces dix unités permettent d'atteindre 1060, ce qui suffit largement aux usages physiques normaux. C'est le système recommandé en 1948 par la neuvième conférence générale des poids et mesures (et rendu légal en France par le décret 61-501 du 3 mai 1961). Ce système régulier est celui dit de l'échelle longue. Les pays anglo-saxons tendent à utiliser un système irrégulier, l'échelle courte, où un billion vaut 109 et un trillion 1012 (les autres unités étant sans applications pratiques).

Article détaillé : Échelles longue et courte.

Les billiards, trilliards,... d'utilisation moins fréquente, se forment régulièrement sur les préfixes précédents: de manière régulière, un X-illiard vaut mille X-illions.

Au delà de dix, les noms sont régulièrement composés en utilisant comme préfixe le terme latin désignant le rang. La difficulté est alors de savoir compter en latin, et les termes correspondants souffrent souvent d'une orthographe mal stabilisée. Ainsi, on peut noter que le décret français introduit l'orthographe quatrillion au lieu du quadrillion traditionnel, sans que l'on puisse savoir si c'est un changement délibéré ou une simple erreur typographique.

Normalisation proposée par Conway et Wechsler

Proposé par John Horton Conway et Allan Wechsler, ce système régularise et prolonge celui de Nicolas Chuquet. La première étape de son système consiste à normaliser l'écriture des préfixes latins, de 1 à 999 (dans le tableau qui suit, les tirets ne sont destinés qu'à faciliter la lecture, et ne font pas partie du nom de nombre).

N° Unité isolée Unité préfixe Dizaine Centaine
1 mi- un- (n)déci- (n)(x)centi-
2 bi- duo- (n)vinginti- (n)du-centi-
3 tri- tre(s)- (n)(s)tri-ginta- (n)(s)tre-centi-
4 quadri- quattuor- (n)(s)quadra-ginta- (n)(s)quadri-ngenti-
5 quinti- quinqua- (n)(s)quinqua-ginta- (n)(s)qui-ngenti-
6 sexti- se(x)(s)- (n)sexa-ginta- (n)ses-centi-
7 septi- septe(m)(n)- (n)septua-ginta- (n)septi-ngenti-
8 octi- octo- (m)(x)octo-ginta- (m)(x)octi-ngenti-
9 noni- nove(m)(n)- nona-ginta- no-ngenti-

Les radicaux des unités peuvent prendre ou perdre des consonnes de liaisons:

  • tre devient tres devant les mots précédés d'un s: ainsi, 303=trestrecenti.
  • se devient ses devant les mots précédés d'un s: ainsi, 306=sestrecenti.
  • se devient sex devant les mots précédés d'un x: ainsi, 106=sexcenti, tandis que 600 = sescenti.
  • septe devient septem devant les mots précédés d'un m, et septen devant les mots précédés d'un n: ainsi, 107=septencenti et 87=septemoctoginta.
  • De même, nove devient novem devant les mots précédés d'un m, et noven devant les mots précédés d'un n: ainsi, 109=novencenti et 89=novemoctoginta.

Les chiffres sont énoncés dans l'ordre unité, dizaine, centaine; et quand le chiffre est un zéro, le terme correspondant est simplement omis.

Avec cette construction, un 421-llion s'appelle un un-vinginti-quadringenti-llion.

Extension proposée par Conway

Dans la même publication, Conway propose de construire les radicaux latins pour les nombres supérieurs à mille de la manière suivante :

  • Soit N le préfixe latin recherché pour écrire un N-illion.
  • Regrouper les chiffres de N par blocs de trois chiffres.
  • Utiliser le codage précédent pour chacun des blocs de trois chiffres, ou ni-lli si les trois chiffres sont nuls.
  • Intercaler lli entre chaque bloc ainsi obtenu.

Ainsi, avec cette méthode, un 3_000_102-llion s'appelle un tri-lli-ni-lli-duo-centi-lli-on.

Autres systèmes de grands nombres

Système Gillion

Proposé par Russ Rowlett, basé sur les préfixes numériques grecs, et les puissances de mille :

Valeur Expression Nom
103 10001 Mille
106 10002 Million
109 10003 Milliard
1012 10004 Tetrillion
1015 10005 Pentillion
1018 10006 Hexillion
1021 10007 Heptillion
1024 10008 Oktillion
1027 10009 Ennillion
1030 100010 Dekillion
Valeur Expression Nom
1033 100011 Hendekillion
1036 100012 Dodekillion
1039 100013 Trisdekillion
1042 100014 Tetradekillion
1045 100015 Pentadekillion
1048 100016 Hexadekillion
1051 100017 Heptadekillion
1054 100018 Oktadekillion
1057 100019 Enneadekillion
1060 100020 Icosillion
Valeur Expression Nom
1063 100021 Icosihenillion
1066 100022 Icosidillion
1069 100023 Icositrillion
1072 100024 Icositetrillion
1075 100025 Icosipentillion
1078 100026 Icosihexillion
1081 100027 Icosiheptillion
1084 100028 Icosioktillion
1087 100029 Icosiennillion
1090 100030 Triacontillion

Système Myriade

Proposé par Donald E. Knuth, ce système est une autre manière de généraliser les myriades grecques: au lieu que chaque « ordre de grandeur » corresponde à un regroupement de quatre chiffres, comme pour Archimède, Knuth considère que chaque ordre de grandeur peut avoir deux fois plus de chiffres que le précédent.

Au delà des noms où l'on reconnaît la présence du « y » caractéristique, il utilise des séparateurs différents pour des groupes de 4, 8, 16, 32 ou 64 chiffres (respectivement la virgule, le point-virgule, et les deux points, l'espace et l'apostrophe ; le séparateur décimal reste le point dans cette notation). Ils sont formés sur des puissances de deux successives des puissances de dix mille (myriade). Ce système permet d'écrire et nommer des nombres énormes (le premier grand nombre qui ne peut être exprimé avec les dénominations classiques est l'oktyllion, la mille-vingt-quatrième puissance de la myriade). Toutefois, le nom « myriade » reste le plus connu car il correspond à une dénomination historique.

Toutefois les noms sont rarement utilisés car ils sont souvent homonymes et homophones d’autres nombres (y compris en anglais où ces noms ont été définis), et créent de nouvelles ambiguïtés avec les échelles courtes et longues.

Valeur Nom Notation
100 Un 1
101 Dix 10
102 Cent 100
103 Mille 1000
104 Myriade 1,0000
105 Dix myriades 10,0000
106 Cent myriades 100,0000
107 Mille myriades 1000,0000
108 Myllion 1;0000,0000
1012 Myriade de myllions 1,0000;0000,0000
1016 Byllion 1:0000,0000;0000,0000
1024 Myllion de byllions 1;0000,0000:0000,0000;0000,0000
1032 Tryllion 1 0000,0000;0000,0000:0000,0000;0000,0000
1064 Quadryllion 1'0000,0000;0000,0000:0000,0000;0000,0000 0000,0000;0000,0000:0000,0000;0000,0000
10128 Quintyllion
10256 Sextyllion
10512 Septyllion
101024 Octyllion
102048 Nonyllion
104096 Decyllion
108192 Undecyllion
1016,384 Duodecyllion
1032,768 Tredecyllion
1065,536 Quattuordecyllion
10131,072 Quindecyllion
10262,144 Sexdecyllion
10524,288 Septendecyllion
101,048,576 Octodecyllion
102,097,152 Novemdecyllion
104,194,304 Vigintyllion
104,294,967,296 Trigintyllion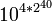
{10}^{\,\! 4 * 2^{40}} Quadragintyllion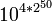
{10}^{\,\! 4 * 2^{50}} Quinquagintyllion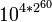
{10}^{\,\! 4 * 2^{60}} Sexagintyllion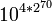
{10}^{\,\! 4 * 2^{70}} Septuagintyllion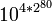
{10}^{\,\! 4 * 2^{80}} Octogintyllion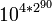
{10}^{\,\! 4 * 2^{90}} Nonagintyllion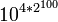
{10}^{\,\! 4 * 2^{100}} Centyllion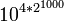
{10}^{\,\! 4 * 2^{1000}} Millyllion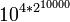
{10}^{\,\! 4 * 2^{10000}} Myryllion

Le système Googol

Les termes googol et googolplex furent inventés par Milton Sirotta, neveu du mathématicien Edward Kasner, qui les introduisit dans une publication de 1940, Mathematics and the Imagination,[1] où il décrit cette invention :

Le terme « googol » a été inventé par un enfant, le neveu du Dr Kasner, alors âgé de huit ans. On lui avait demandé d'imaginer un nom pour un nombre très grand, par exemple un 1 suivi d'une centaine de zéros. Il était sûr que ce nombre n'était pas infini, et tout aussi certain qu'il n'avait pas de nom propre. Il suggéra le terme « googol », et dans la foulée en proposa un autre pour un nombre encore plus grand: le « googolplex ». Un googolplex est beaucoup plus grand qu'un googol, mais reste fini, ce que l'inventeur du terme fit rapidement remarquer. Au départ, la définition proposée était un 1, suivi d'autant de zéro qu'on pourrait en écrire sans tomber de fatigue. C'est certainement ce qui risquerait d'arriver si quelqu'un essaye d'écrire un googolplex, mais deux personnes différentes seraient fatiguées au bout d'un temps différent, et ça n'aurait pas de sens que Carnera soit un meilleur mathématicien que Einstein simplement parce qu'il a une meilleure endurance. Pour cette raison, le googolplex est un nombre spécifique, mais avec tellement de zéros derrière son « un » que le nombre de zéros est lui-même d'un googol.

Par la suite, Conway et Guy [2] ont suggéré comme extension que un N-plex corresponde par convention à 10N. Avec ce système, un googol-plex vaut bien 10googol, et un googolplexplex vaut 10googolplex.

D'autres auteurs ont proposé les formes googolduplex, googoltriplex, etc., pour désigner respectivement 10googolplex, 10googolduplex, et ainsi de suite.

10100 Googol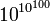
{10}^{\,\!10^{100}} Googolplex
10-N N-minex
10N N-plex

Notes et références

  1. ↑ Kasner, Edward and James Newman, Mathematics and the Imagination, 1940, Simon and Schuster, New York.
  2. ↑ The Book of Numbers, J. H. Conway and R. K. Guy, New York: Springer-Verlag, 1996, pp. 15–16. ISBN 0-387-97993-X.

Voir aussi

Articles connexes

Liens externes

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nom des grands nombres ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Nom Des Grands Nombres de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Nom des grands nombres — Les noms des grands nombres (supérieurs au trillion) ne sont pratiquement jamais utilisés, du moins dans un contexte de communication normale. De nombreux systèmes ont été proposés pour nommer des grands nombres, mais aucun ne semble avoir eu d… …   Wikipédia en Français

  • Liste Des Grands Nombres — En mathématiques, grand nombre n a pas de sens bien défini[1]. Liste de grands nombres finis 10100 est le gogol (101 chiffres) est le gogolplex (un 1 avec 10100 zéros) …   Wikipédia en Français

  • Liste des grands nombres — En mathématiques, grand nombre n a pas de sens bien défini[1]. Liste de grands nombres finis 10100 est le gogol (101 chiffres) est le gogolplex (un 1 avec 10100 zéros) …   Wikipédia en Français

  • Noms des grands nombres — Pour les articles homonymes, voir Grand nombre. Jusqu au trillion, les grands nombres sont généralement nommés (en français) selon deux systèmes : les échelles longue et courte (le premier étant de loin le plus utilisé, et d ailleurs le seul …   Wikipédia en Français

  • Liste de grands nombres — En mathématiques, grand nombre n a pas de sens bien défini[1] : d une part, l ensemble des grands nombres entiers admettrait un plus petit élément, créant un paradoxe analogue à celui du paradoxe des nombres intéressants ; d autre part …   Wikipédia en Français

  • Nombres En Français — Cet article traite de la dénomination littérale des nombres en langue française. Sommaire 1 Adjectifs ou noms numéraux les plus courants 2 Variantes des adjectifs selon les pays 2.1 France et Canada …   Wikipédia en Français

  • Nombres en francais — Nombres en français Cet article traite de la dénomination littérale des nombres en langue française. Sommaire 1 Adjectifs ou noms numéraux les plus courants 2 Variantes des adjectifs selon les pays 2.1 France et Canada …   Wikipédia en Français

  • Nombres en français — Cet article traite de la dénomination littérale des nombres en langue française. Sommaire 1 Adjectifs ou noms numéraux les plus courants 2 Variantes des adjectifs 2.1 France et Canada …   Wikipédia en Français

  • Nombres 2 000 à 2 999 — Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de deux mille (2 000) à deux mille neuf cent quatre vingt dix neuf (2 999). Sommaire 1 Nombres dans le 2e millier (2 000 2 999) 1.1… …   Wikipédia en Français

  • Liste Des Nombres — Ceci est une liste d articles concernant les nombres. Sommaire 1 Nombres rationnels 1.1 Entiers naturels remarquables 1.2 Puissances de dix 1.3 Entiers relatifs …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”