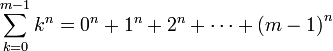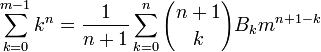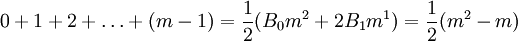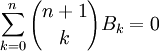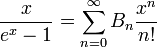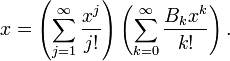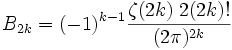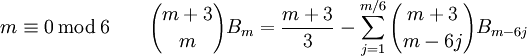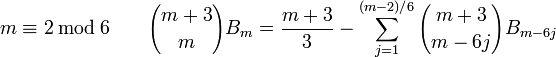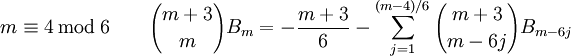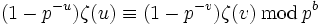- Nombres de Bernoulli
-
Nombre de Bernoulli
En mathématiques, les nombres de Bernoulli, notés
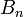 , ont d'abord été étudiés en cherchant des formules pour exprimer les sommes du type :
, ont d'abord été étudiés en cherchant des formules pour exprimer les sommes du type :pour différentes valeurs de l'entier n.
Sommaire
Introduction
De telles expressions sont toujours des polynômes en m, de degré
 dont les coefficients sont liés aux nombres de Bernoulli de la façon suivante :
dont les coefficients sont liés aux nombres de Bernoulli de la façon suivante :Par exemple, en donnant à n la valeur 1, on obtient :
Les nombres de Bernoulli ont d'abord été étudiés par Jacques Bernoulli, ce qui a conduit Abraham de Moivre à leur donner le nom que nous connaissons aujourd'hui.
Il est possible de calculer les nombres de Bernoulli en utilisant la formule de récurrence suivante :
en plus de la condition initiale :
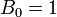 .
.Les nombres de Bernoulli peuvent aussi être définis en utilisant la technique des fonctions génératrices. Leur fonction génératrice exponentielle est
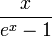 , de telle sorte que :
, de telle sorte que :pour tout x de valeur absolue inférieure à
 (le rayon de convergence de cette série entière).
(le rayon de convergence de cette série entière).Ces définitions peuvent être montrées comme équivalentes en utilisant l'induction mathématique. La condition initiale B0 = 1 est immédiate à partir de la règle de L'Hôpital. Pour obtenir la récurrence, on multiplie les deux cotés de l'équation par ex − 1. Alors, en utilisant les séries de Taylor pour la fonction exponentielle,
En développant ceci comme un produit de Cauchy et en réarrangeant légèrement, on obtient
Il est clair, à partir de cette dernière égalité, que les coefficients dans cette série de puissances satisfont la même récurrence en tant que nombres de Bernoulli.
Parfois, la notation
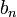 est utilisée pour distinguer les nombres de Bernoulli des nombres de Bell.
est utilisée pour distinguer les nombres de Bernoulli des nombres de Bell.Valeurs
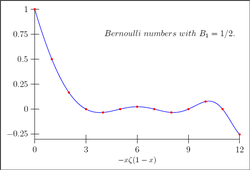
Les premiers nombres de Bernoulli sont les suivants :
n Bn 0 1 1 −1/2 = −0,5 2 1/6 ≈ 0,1667 4 −1/30 ≈ −0,0333 6 1/42 ≈ 0,02381 8 −1/30 ≈ −0,0333 10 5/66 ≈ 0,07576 12 −691/2730 ≈ −0,2531 14 7/6 ≈ 1,1667 n Bn 16 −3617/510 ≈ −7,0922 18 43867/798 ≈ 54,9712 20 −174611/330 ≈ −529,124 22 854513/138 ≈ 6192,12 24 −236364091/2730 ≈ −86580,3 26 8553103/6 ≈ 1425517 28 −23749461029/870 ≈ −27298231 30 8615841276005/14322 ≈ 601580874 32 −7709321041217/510 ≈ −15116315767 On peut démontrer que
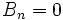 lorsque n est impair et différent de 1.
lorsque n est impair et différent de 1.L'apparition de la valeur de
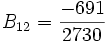 montre bien que la valeur des nombres de Bernoulli ne peuvent pas être décrits simplement ; en fait, ce sont essentiellement des valeurs de la fonction ζ de Riemann pour des valeurs entières négatives de la variable, (puisque
montre bien que la valeur des nombres de Bernoulli ne peuvent pas être décrits simplement ; en fait, ce sont essentiellement des valeurs de la fonction ζ de Riemann pour des valeurs entières négatives de la variable, (puisque 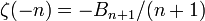 pour tous les entiers positifs n), et sont en conséquence, associés à des propriétés profondes de la théorie des nombres, et ne peuvent pas espérer avoir de formulation triviale.
pour tous les entiers positifs n), et sont en conséquence, associés à des propriétés profondes de la théorie des nombres, et ne peuvent pas espérer avoir de formulation triviale.Les nombres de Bernoulli apparaissent également dans le développement en série de Taylor des fonctions tangentes circulaire et hyperbolique, dans la formule d'Euler-Maclaurin ainsi que dans des expressions de certaines valeurs de la fonction zeta de Riemann.
Identités remarquables
Leonhard Euler a exprimé les nombres de Bernoulli en termes de fonction zeta de Riemann :
Les relations suivantes, dues à Ramanujan, fournissent une méthode plus efficace pour le calcul des nombres de Bernoulli :
Une identité de Carlitz :
Propriétés arithmétiques
Il est possible d'exprimer les nombres de Bernoulli grâce à la fonction zêta de Riemann de la façon suivante :
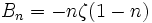 ;
;
C'est la raison pour laquelle les nombres de Bernoulli possèdent des propriétés arithmétiques profondes, comme l'a découvert Kummer dans ses travaux sur le dernier théorème de Fermat.
Les propriétés de divisibilité des nombres de Bernoulli sont liées aux groupes des classes d'idéaux des corps cyclotomiques par un théorème de Kummer et son renforcement dans le théorème de Herbrand-Ribet, et aux nombres de classes des corps quadratiques par la congruence d'Ankeny-Artin-Chowla. Nous avons aussi un lien de parenté avec la K-théorie algébrique; si
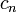 est le numérateur de
est le numérateur de 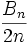 , alors l'ordre de
, alors l'ordre de 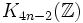 est
est 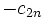 si n est pair, et
si n est pair, et 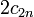 si n est impair.
si n est impair.Le théorème de von Staudt-Clausen est aussi relié à la divisibilité. Il énonce ceci : si nous ajoutons
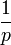 à
à 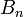 pour chaque nombre premier p tel que p − 1 divise n, nous obtenons un nombre entier. Ce fait nous permet immédiatement de caractériser les dénominateurs des nombres de Bernoulli différents de zéro
pour chaque nombre premier p tel que p − 1 divise n, nous obtenons un nombre entier. Ce fait nous permet immédiatement de caractériser les dénominateurs des nombres de Bernoulli différents de zéro 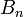 comme le produit de tous les nombres premiers p tels que p − 1 divise n; en conséquence, les dénominateurs sont sans carré et divisibles par 6.
comme le produit de tous les nombres premiers p tels que p − 1 divise n; en conséquence, les dénominateurs sont sans carré et divisibles par 6.La conjecture d'Agoh-Giuga postule que p est un nombre premier si et seulement si
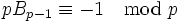 .
.Continuité p-adique
Une propriété de congruence spécialement importante des nombres de Bernoulli peut être caractérisée comme une propriété de continuité p-adique. Si b, m et n sont des nombres entiers positifs tels que m et n ne sont pas divisibles par
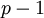 et
et  , alors
, alors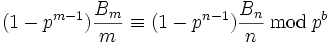 .
.
Puisque
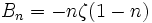 , ceci peut être aussi écrit
, ceci peut être aussi écritoù
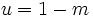 et
et  , c’est-à-dire u et v sont négatifs et non congru à 1 mod p-1. Ceci nous indique que la fonction zeta de Riemann, avec
, c’est-à-dire u et v sont négatifs et non congru à 1 mod p-1. Ceci nous indique que la fonction zeta de Riemann, avec 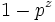 prise hors de la formule du produit d'Euler, est continue pour les nombres p-adiques sur les nombres entiers négatifs congrus mod p-1, en particulier
prise hors de la formule du produit d'Euler, est continue pour les nombres p-adiques sur les nombres entiers négatifs congrus mod p-1, en particulier 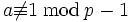 , et donc, peut être étendu à une fonction continue
, et donc, peut être étendu à une fonction continue 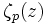 pour tous les nombres entiers p-adiques
pour tous les nombres entiers p-adiques 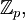 la fonction zeta p-adique.
la fonction zeta p-adique.Propriétés géométriques
La formule de Kervaire-Milnor pour l'ordre du groupe cyclique des classes de difféomorphismes des (4n−1)-sphères exotiques qui bornent des variétés parallélisables pour
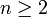 impliquent les nombres de Bernoulli : si B est le numérateur de
impliquent les nombres de Bernoulli : si B est le numérateur de 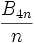 , alors
, alors 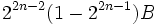 est le nombre de ces sphères exotiques. (La formule dans les articles topologiques diffère parce que les topologistes utilisent une convention différente pour nommer les nombres de Bernoulli ; cet article utilise la convention de la théorie des nombres).
est le nombre de ces sphères exotiques. (La formule dans les articles topologiques diffère parce que les topologistes utilisent une convention différente pour nommer les nombres de Bernoulli ; cet article utilise la convention de la théorie des nombres).Bibliographie
- John H. Conway, Richard K. Guy; Le livre des Nombres (Eyrolles, 1998 - ISBN 2-212-03638-8)
- Portail des mathématiques
Catégories : Analyse réelle | Suite d'entiers
Wikimedia Foundation. 2010.