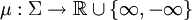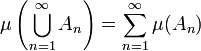Mesure Signée

Mesure Signée

Mesure signée

En mathématiques, on définit une mesure signée comme étant une mesure pouvant prendre des valeurs négatives.

Définition

Soit un espace mesurable (X, Σ), c'est-à-dire un ensemble X muni d'une tribu Σ, une mesure signée est une fonction

\mu:\Sigma\to \mathbb {R}\cup\{\infty,-\infty\}

qui est également sigma additive, c'est-à-dire remplissant la propriété:

\mu\left(\bigcup_{n=1}^\infty A_n\right) = \sum_{n=1}^\infty \mu(A_n)

pour toute suite A1, A2, ..., An, ... d'ensembles disjoints dans Σ. A noter qu'une mesure signée peut prendre comme valeur +∞ mais pas −∞, ou inversement, puisque l'expression ∞−∞ n'est pas définie (voir Droite réelle achevée), et doit donc être évitée.

Pour clarifier, on explicitera le terme de mesure non-négatives pour des mesures n'ayant pas de valeurs négatives, a contrario des mesures signées pouvant prendre des valeurs négatives. On supposera que la valeur -∞ n'est prise par aucune mesure signée (le cas inverse se traitant de manière similaire).

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Mesure sign%C3%A9e ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Mesure Signée de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Mesure signee — Mesure signée En mathématiques, on définit une mesure signée comme étant une mesure pouvant prendre des valeurs négatives. Définition Soit un espace mesurable (X, Σ), c est à dire un ensemble X muni d une tribu Σ, une mesure signée est une… …   Wikipédia en Français

  • Mesure signée — En mathématiques, on définit une mesure signée comme étant une mesure pouvant prendre des valeurs négatives. Définition Soit un espace mesurable (X, Σ), c est à dire un ensemble X muni d une tribu Σ, une mesure signée est une fonction qui est… …   Wikipédia en Français

  • Mesure (mathematiques) — Mesure (mathématiques) Pour les articles homonymes, voir mesure. En mathématiques, une mesure est une fonction qui associe une « longueur », un « volume » ou encore une « probabilité » à certaines parties d un… …   Wikipédia en Français

  • Mesure (mathématique) — Mesure (mathématiques) Pour les articles homonymes, voir mesure. En mathématiques, une mesure est une fonction qui associe une « longueur », un « volume » ou encore une « probabilité » à certaines parties d un… …   Wikipédia en Français

  • Mesure de dénombrement — Mesure (mathématiques) Pour les articles homonymes, voir mesure. En mathématiques, une mesure est une fonction qui associe une « longueur », un « volume » ou encore une « probabilité » à certaines parties d un… …   Wikipédia en Français

  • Mesure (mathématiques) — Pour les articles homonymes, voir mesure. Pour une introduction à cette notion, consulter l article : Superficie. En mathématiques, une mesure positive (ou simplement mesure quand il n y a pas de risque de confusion) est une fonction qui… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Champ (mathématiques) — Pour les articles homonymes, voir Champ. Un champ est une application qui associe aux points d un objet, généralement multidimensionnel, des valeurs scalaires, vectorielles ou tensorielles. Sommaire 1 Vision physique et vision mathématique des… …   Wikipédia en Français

  • Courant (Mathématiques) — Sommaire 1 Introduction 2 Topologie 3 Cas particuliers 4 Exemples 5 Bibliographie …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”