Sigma-algèbre

En mathématiques, une tribu ou σ-algèbre 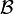sur un ensemble Ω est un ensemble de parties de Ω contenant la partie vide, stable par complémentarité et par union dénombrable. La notion de σ-algèbre est plus forte que celle d'algèbre de Boole, où l'on impose simplement la stabilité par réunion finie. Les tribus sont principalement utilisées afin de définir des mesures sur Ω et ainsi permettre l'intégration telle que Lebesgue l'a créée. Le concept est important en analyse et en théorie des probabilités.

Sommaire 1 Définition 2 Propriétés 3 Remarque 4 Exemples 5 Tribu engendrée 6 Tribu borélienne 7 Tribu produit 8 Étymologie 9 Voir aussi 9.1 Articles connexes 9.2 Liens externes 9.3 Bibliographie 9.4 Références

Définition

Soit 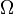un ensemble. On appelle tribu (ou σ-algèbre) sur 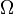un ensemble 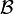de parties de 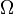qui vérifie :

1. l'ensemble vide est dans
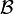
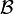2. est stable par complémentaire
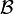3. est stable par union dénombrable

Formellement :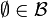

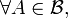
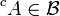
1. 
2. 
3. si 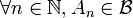alors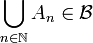

Le couple 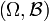est appelé espace mesurable ou espace probabilisable en fonction du contexte. La notion de mesure est définie à l'intérieur d'un espace mesurable et celle de probabilité à l'intérieur d'un espace probabilisable.

Propriétés

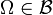• (d'après 1 et 2)
• une tribu est également stable pour l'opération d'intersection dénombrable (d'après 2 et 3) :
  si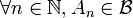 alors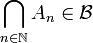
• Si 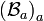est une famille de tribus sur Ω, alors 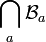est aussi une tribu sur Ω.

Remarque

Si 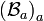est une famille de tribus sur Ω, alors 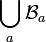n'est pas une tribu sur Ω en général.

Par exemple, pour Ω = {1,2,3}, en prenant 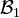engendrée (voir ci-dessous) par {1,2} et {3} et 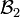par {1} et {2,3}, on remarque que {1,2}∩{2,3}={2} n'est pas dans .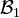

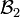Exemples

• tribu triviale (aussi appelée discrète) : 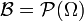où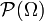 représente l'ensemble de toutes les parties de Ω
• tribu grossière :

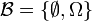
La tribu triviale est la plus grande possible, et la tribu grossière la plus petite possible, au sens de l'inclusion.

• Si Ω = {a,b,c,d} alors 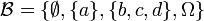est une tribu sur Ω. C'est la plus petite tribu contenant l'ensemble {a}.

Tribu engendrée

Si U est un ensemble arbitraire de parties de Ω alors il existe une plus petite tribu (au sens de l'inclusion) contenant U, notée σ(U) et appelée la tribu engendrée par U.

D'abord remarquons qu'il existe une tribu sur Ω qui contient U, la tribu discrète sur Ω. Soit Φ l'ensemble de toutes les tribus sur Ω qui contiennent U (cela signifie qu'une tribu 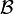sur Ω appartient à Φ si et seulement si U est un sous-ensemble de 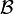). Alors nous définissons σ(U) comme étant l'intersection de toutes les tribus de Φ : σ(U) est la plus petite tribu sur Ω contenant U ; ses éléments sont tous les ensembles qui peuvent être obtenus à partir des éléments de U en utilisant les opérations d'intersection, de réunion dénombrable, ou de passage au complémentaire transfiniment.

Exemples :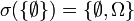

• 
• Soi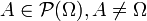t et 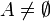, alors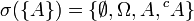
• Soit 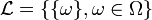l'ensemble des singletons de l'univers 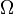. On a 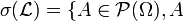ou 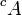dénombrable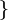

Tribu borélienne

Cela nous mène à l'exemple le plus important : la tribu de Borel sur n'importe quel espace topologique, qui est la tribu engendrée par les ensembles ouverts (ou, de manière équivalente, par les ensembles fermés), appelée tribu borélienne. Cette tribu n'est pas, en général, l'ensemble de toutes les parties ; par exemple, la tribu borélienne de Rⁿ a la puissance du continu, alors que P(Rⁿ) a une puissance strictement supérieure.

Sur l'espace euclidien 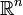, une autre tribu importante : celle des ensembles Lebesgue-mesurables. Cette tribu contient « plus » d'ensembles que la tribu de Borel sur 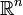et est privilégiée dans la théorie de l'intégration. Elle ne contient pas non plus l'ensemble des parties de 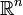, mais l'argument de cardinalité ne suffit plus ; voir Ensemble non mesurable.

Tribu produit

Soi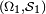t et 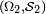deux ensembles, chacun muni d'une tribu. La tribu-produit 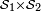est la tribu de parties du produit cartésien 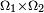engendrée par les pavés 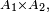où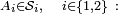

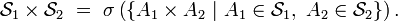
Étymologie

Il semble que c'est Nicolas Bourbaki qui ait proposé (chapitre IX de l'opus Topologie générale) l'appellation tribu^[1][2] le premier. Il est avancé^[1] que Bourbaki n'était pas féru de théorie de la mesure, d'où une certaine propension à nommer avec des noms primitifs les objets de cette théorie (tribu, clan). D'un autre côté, tous les mots synonymes (groupe, corps...) sont déjà pris, il fallait bien trouver un mot qui fasse sens. Dont acte.

Voir aussi

Articles connexes

• Paradoxe de Banach-Tarski

Liens externes

• cours en ligne sur les ensembles mesurables

Bibliographie

• Théorie de l'intégration de Marc Briane et Gilles Pagès, édition Vuibert, chapitre 4

Références

• Portail des mathématiques
• Portail des probabilités et des statistiques