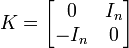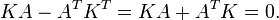Matrice de Hamilton
- Matrice de Hamilton
-
Matrice hamiltonienne
En mathématiques, une matrice hamiltonienne (ou de Hamilton) A est une matrice réelle 2n×2n satisfaisant la condition que le produit KA soit symétrique, K étant la matrice antisymétrique :
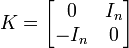
et In étant la matrice identité n×n. En d'autres termes, A est hamiltonienne si et seulement si :
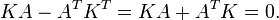
Dans l'espace vectoriel des matrices 2n×2n, les matrices hamiltoniennes forment un sous-espace vectoriel de dimension 2n2 + n.
Propriétés
- Soit M une matrice par bloc 2n×2n donnée par :
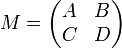
- où A,B,C,D sont des matrices n×n. Alors M est une matrice hamiltonienne à condition que B,C soient symétriques et que A + DT = 0.
- La transposée d'une matrice hamiltonienne est hamiltonienne.
- La trace d'une matrice hamiltonienne est nulle.
- Le commutateur de deux matrices hamiltoniennes est hamiltonien.
- Les valeurs propres de M sont symétriques par rapport à l'axe imaginaire.
L'espace des matrices hamiltoniennes est une algèbre de Lie 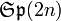 [1].
[1].
Opérateurs hamiltoniens
Soit V un espace vectoriel, doté d'une forme symplectique Ω. Une application linéaire 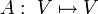 est appelée opérateur hamiltonien par rapport à Ω si l'application
est appelée opérateur hamiltonien par rapport à Ω si l'application 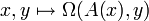 est symétrique. De manière équivalente, elle doit satisfaire :
est symétrique. De manière équivalente, elle doit satisfaire :
- Ω(A(x),y) = − Ω(x,A(y))
Soit une base e1,...e2n de V telle que Ω soit écrite 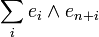 . un opérateur linéaire est hamiltonien par rapport à Ω si et seulement si sa matrice dans cette base est hamiltonienne[2]. Cette définition implique que le carré d'une matrice hamiltonienne est anti-hamiltonien. L'exponentiel d'une matrice hamiltonienne est symplectique, et le logarithme d'une matrice symplectique est hamiltonien.
. un opérateur linéaire est hamiltonien par rapport à Ω si et seulement si sa matrice dans cette base est hamiltonienne[2]. Cette définition implique que le carré d'une matrice hamiltonienne est anti-hamiltonien. L'exponentiel d'une matrice hamiltonienne est symplectique, et le logarithme d'une matrice symplectique est hamiltonien.
Voir aussi
Références
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Hamiltonian matrix ».
 Portail des mathématiques
Portail des mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Matrice de Hamilton de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Matrice quaternionique — Une matrice quaternionique est une matrice dont les éléments sont des quaternions. Sommaire 1 Produit de matrices quaternioniques 1.1 Produit hamiltonien 1.2 Produit octonionique … Wikipédia en Français
Matrice (algèbre) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice (mathematiques) — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice carrée — Matrice (mathématiques) Pour les articles homonymes, voir Matrice. En mathématiques, les matrices servent à interpréter en termes calculatoire … Wikipédia en Français
Matrice Diagonalisable — En algèbre linéaire, une matrice carrée M d ordre n ( ) à coefficients dans un corps commutatif K, est dite diagonalisable si elle est semblable à une matrice diagonale, c est à dire s il existe une matrice inversible P et une matrice diagonale D … Wikipédia en Français
Matrice Nilpotente — Une matrice nilpotente est une matrice dont il existe une puissance égale à la matrice nulle. Elle correspond à la notion d endomorphisme nilpotent. Cette notion joue un rôle important dans le monde des matrices. En effet, pour un maniement plus… … Wikipédia en Français
Matrice De Transition — Définition Notons l ensemble des applications bornées de E dans On appelle matrice de transition sur E une famille telle que Ainsi, une matrice positive … Wikipédia en Français
Matrice (mathématiques) — Pour les articles homonymes, voir Matrice. En mathématiques, les matrices sont des tableaux de nombres qui servent à interpréter en termes calculatoires et donc opérationnels les résultats … Wikipédia en Français
Matrice diagonalisable — Exemple de matrice diagonalisable sur le corps des complexes mais pas sur celui des réels, son polynôme caractéristique étant X2 + 1. En mathématiques, une matrice diagonalisable est une matrice carrée semblable à une matrice diagonale. Cette p … Wikipédia en Français
Matrice nilpotente — Une matrice nilpotente est une matrice dont il existe une puissance égale à la matrice nulle. Elle correspond à la notion d endomorphisme nilpotent sur un espace vectoriel de dimension finie. Cette notion facilite souvent le calcul matriciel. En… … Wikipédia en Français
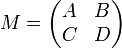
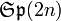 [1].
[1].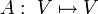 est appelée opérateur hamiltonien par rapport à Ω si l'application
est appelée opérateur hamiltonien par rapport à Ω si l'application 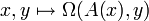 est symétrique. De manière équivalente, elle doit satisfaire :
est symétrique. De manière équivalente, elle doit satisfaire :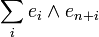 . un opérateur linéaire est hamiltonien par rapport à Ω si et seulement si sa matrice dans cette base est hamiltonienne[2]. Cette définition implique que le carré d'une matrice hamiltonienne est anti-hamiltonien. L'exponentiel d'une matrice hamiltonienne est symplectique, et le logarithme d'une matrice symplectique est hamiltonien.
. un opérateur linéaire est hamiltonien par rapport à Ω si et seulement si sa matrice dans cette base est hamiltonienne[2]. Cette définition implique que le carré d'une matrice hamiltonienne est anti-hamiltonien. L'exponentiel d'une matrice hamiltonienne est symplectique, et le logarithme d'une matrice symplectique est hamiltonien.