Forme Symplectique

Forme symplectique

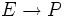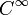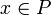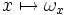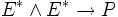En géométrie différentielle, sur un fibré vectoriel réel $E\rightarrow P$ , une forme symplectique $ω$ est la donnée d'une famille de formes bilinéaires non dégénérées $ω x$ sur les fibres $E x$ dépendant de manière $C^{\infty}$ du point $x \in P$ . De manière plus rigoureuse, une forme symplectique est une section globale $x\mapsto \omega_x$ de $E^*\wedge E^*\rightarrow P$ qui soit en tout point non dégénérée.

Cependant, sur une variété différentielle $M$ , une forme symplectique $ω$ est une 2-forme différentielle non dégénérée et fermée. Plus explicitement, on impose les conditions suivantes :

La forme $ω$ est non dégénérée, id est, en tout point $x$ , la forme bilinéaire antisymétrique $ω x$ est non dégénérée.

La forme $ω$ est fermée, au sens où : $d ω$ .

En particulier, $(T M,ω)$ est un fibré symplectique, mais la définition d'une forme symplectique ne se limite pas à cette simple propriété. La condition d'être fermée implique l'unicité locale fournie par le théorème de Darboux.

Exemples

Si 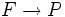$F\rightarrow P$ est un fibré vectoriel, alors il existe une forme symplectique sur le fibré vectoriel 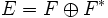$E=F\oplus F^*$ donnée par :

$\omega\left[f_1\oplus f_1^*,f_2\oplus f_2^*\right]=f_1^*(f_2)-f_2^*(f_1)$

Ce premier exemple montre la naturalité des formes symplectiques. Contrairement aux métriques riemanniennes, leur existence est mal comprise, mais au moins, elles viennent naturellement.

Si (M,ω) est une variété symplectique de dimension 2n, et que P est une sous-variété différentielle de M, alors :
- Le fibré tangent de $M$ se restreint en un fibré de rang $2 n$ sur $P$ , noté 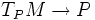$T_PM\rightarrow P$ . Et $(T P M,ω)$ est un fibré symplectique.
- Si en tout point x de P, la forme bilineaire $ω x$ est non degeneree en restriction a l'espace tangent $T x P$ , alors, $ι * ω$ est une forme symplectique sur P.

Existence

L'existence des formes symplectiques sur les varietes differentielles est une question ouverte.

Ce document provient de « Forme symplectique ».

Catégorie : Géométrie symplectique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Forme Symplectique de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Forme symplectique — En géométrie différentielle, sur un fibré vectoriel réel E → P , une forme symplectique ω est la donnée d une famille de formes bilinéaires non dégénérées alternées ωx sur les fibres Ex dépendant de manière C∞ du point x de P. De manière plus… … Wikipédia en Français
Forme Volume — En géométrie différentielle, une forme volume généralise la notion de déterminant aux variétés différentielles. Elle définit une mesure sur la variété, permet le calcul des volumes généralisés, et la définition générale des orientations. Une… … Wikipédia en Français
Forme d'aire — Forme volume En géométrie différentielle, une forme volume généralise la notion de déterminant aux variétés différentielles. Elle définit une mesure sur la variété, permet le calcul des volumes généralisés, et la définition générale des… … Wikipédia en Français
Forme De Liouville — En géométrie différentielle, la forme de Liouville est une 1 forme différentielle naturelle sur les variétés cotangentes. Sa différentielle est une forme symplectique Elle joue un rôle central en mécanique classique. L étude de la géométrie des… … Wikipédia en Français
Forme de liouville — En géométrie différentielle, la forme de Liouville est une 1 forme différentielle naturelle sur les variétés cotangentes. Sa différentielle est une forme symplectique Elle joue un rôle central en mécanique classique. L étude de la géométrie des… … Wikipédia en Français
Forme volume — En géométrie différentielle, une forme volume généralise la notion de déterminant aux variétés différentielles. Elle définit une mesure sur la variété, permet le calcul des volumes généralisés, et la définition générale des orientations. Une… … Wikipédia en Français
Forme de Liouville — En géométrie différentielle, la forme de Liouville est une 1 forme différentielle naturelle sur les variétés cotangentes. Sa différentielle est une forme symplectique Elle joue un rôle central en mécanique classique. L étude de la géométrie des… … Wikipédia en Français
FORME — L’histoire du concept de forme et des théories de la forme est des plus singulières. Nous vivons dans un monde constitué de formes naturelles. Celles ci sont omniprésentes dans notre environnement et dans les représentations que nous nous en… … Encyclopédie Universelle
symplectique — [ sɛ̃plɛktik ] adj. • 1842 minér.; lat. sc. symplecticus; gr. sumplektikos « qui entrelace » ♦ Didact. Qui est entrelacé (avec un autre corps, une autre partie). ⇒SYMPLECTIQUE, adj. et subst. masc. I. Adj., HIST. NAT. Qui est entrelacé avec un… … Encyclopédie Universelle
Forme de contact — Géométrie de contact Structure standard sur ℝ3 : champ de plans La géométrie de contact est la partie de la géométrie différentielle qui étudie les formes et structures de contact. Elle entretient d étroits liens avec la géométrie… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Forme Symplectique