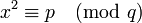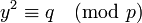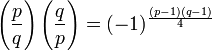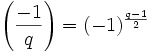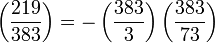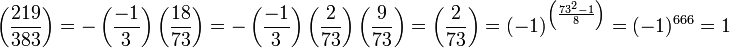Loi de reciprocite quadratique

Loi de reciprocite quadratique

Loi de réciprocité quadratique

En mathématiques, et plus précisément en théorie algébrique des nombres, la loi de réciprocité quadratique, conjecturée par Euler et Legendre et correctement démontrée pour la première fois par Gauss, établit un lien entre la résolubilité de deux équations diophantiennes quadratiques voisines d'arithmétique modulaire. Cette loi permet en fait de déterminer la résolubilité de n'importe quelle équation quadratique en arithmétique modulaire.

Sommaire

Énoncés

Premier énoncé

Étant donné des nombres premiers distincts p et q impairs, la loi de réciprocité quadratique comprend deux résultats qui dépendent chacun des valeurs respectives de p et de q :

  • si au moins l'un des nombres p et q est congru à 1 modulo 4, alors l'équation d'inconnue x :
x^2\equiv p \pmod{q}
a une solution si et seulement si l'équation d'inconnue y :
y^2\equiv q \pmod{p}
a une solution (les deux solutions sont en général différentes).
  • si p et q sont congrus à 3 modulo 4, alors l'équation d'inconnue x :
x^2\equiv p \pmod{q}
a une solution si et seulement si l'équation d'inconnue y :
y^2\equiv q \pmod{p}
n'a pas de solution.

Énoncé avec le Symbole de Legendre

En utilisant le symbole de Legendre, ces deux résultats peuvent être résumés par l'énoncé unique suivant :

\left(\frac{p}{q}\right) \left(\frac{q}{p}\right) = (-1)^{\frac{(p-1)(q-1)}{4}}

De plus -1 est un résidu quadratique modulo p si et seulement si le reste de la division de p par 4 est égal à 1. Et 2 est un résidu quadratique modulo p si et seulement si le reste de la division de p par 8 est égal à 1 ou 7.

Exemples

Avec des nombres premiers

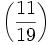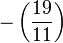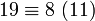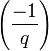Par exemple, si p vaut 11 et q vaut 19, il est possible de ramener le calcul de \left(\frac{11}{19}\right) à celui de -\left(\frac{19}{11}\right), qui est égal à -\left(\frac{8}{11}\right) (puisque 19\equiv 8\ (11)). Pour aller plus loin, nous avons besoin de propriétés supplémentaires qui permettent de calculer \left(\frac{2}{q}\right) et \left(\frac{-1}{q}\right) explicitement, par exemple :

\left(\frac{-1}{q}\right) = (-1)^{\frac{q-1}{2}}

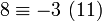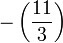En utilisant cela, nous ramenons successivement le calcul de -\left(\frac{8}{11}\right) à -\left(\frac{-3}{11}\right) (car 8\equiv -3\ (11)), puis à -\left(\frac{11}{3}\right) et enfin à 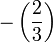-\left(\frac{2}{3}\right), ce qui termine le calcul, puisque 2 n'est pas résidu quadratique modulo 3.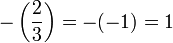-\left(\frac{2}{3}\right)=-(-1)= 1. Conclusion: Le résultat étant 1, on en déduit que 11 est résidu quadratique modulo 19. D'ailleurs on le vérifie immédiatement :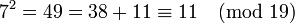 7^2 =49=38+11 \equiv 11 \pmod{19}

Cas général

Déterminons si 219 est un carré modulo 383. Les propriétés du symbole de Legendre montrent que :

\left(\frac{219}{383}\right)= \left(\frac{3}{383}\right)\left(\frac{73}{383}\right)

Une première application de la loi de réciprocité quadratique montre que :

\left(\frac{219}{383}\right)= -\left(\frac{383}{3}\right)\left(\frac{383}{73}\right)

En appliquant encore la loi de réciprocité quadratique et les propriétés du symbole de Legendre, on obtient :

\left(\frac{219}{383}\right)=-\left(\frac{-1}{3}\right)\left(\frac{18}{73}\right) = -\left(\frac{-1}{3}\right) \left(\frac{2}{73}\right) \left(\frac{9}{73}\right) = \left(\frac{2}{73}\right)=(-1)^{\left(\frac{73^2-1}{8}\right)}=(-1)^{666}=1

Outil de démonstration

Si p est un nombre premier, 5 est-il un carré modulo p ? La loi de réciprocité quadratique nous permet d'affirmer que cela arrive lorsque p est lui-même un carré modulo 5, c'est-à-dire quand p\equiv \pm 1 \pmod{5}

Démonstrations de la loi de réciprocité quadratique

Dans un livre publié en 2000, Lemmermeyer expose l'histoire mathématique des lois de réciprocité en couvrant leurs développements et rassemble des citations de la littérature pour 196 différentes démonstrations de cette loi de réciprocité quadratique.

Les premières démonstrations aujourd'hui considérées comme complètes sont publiées par Gauss dans ses Disquisitiones arithmeticae en 1801. Gauss disposait des preuves dès 1796 (à l'âge de 19 ans). La première de ces preuves repose sur un raisonnement par récurrence. Dans sa correspondance avec son élève Ferdinand Eisenstein, Gauss qualifie cette preuve de laborieuse[1].

Une autre démonstration est donnée dans l'article Somme de Gauss. Elle se fonde sur les outils de l'analyse harmonique sur un groupe abélien fini et utilise les caractères des groupes abéliens additif et multiplicatif du corps fini Fp à p éléments.

Une des nombreuses démonstrations, fondée sur un calcul de dénombrement, permit à Thomas Joannes Stieltjes d'élucider le caractère quadratique de -1 et 2 avec une approche élémentaire et élégante[2]. Cette démonstration est proposée ici.

Détails des démonstrations pour -1 et 2

Soit p un nombre premier différent de 2. L'objectif est de déterminer le statut quadratique de -1 et 2 dans le corps fini Z/pZ ou encore Fp. La notation Fp désigne l'unique corps fini contenant p éléments, à un isomorphisme près. Ici, Fp* désigne le groupe multiplicatif du corps Fp. C'est un groupe cyclique contenant p - 1 éléments (cf l'article Anneau Z/nZ). Comme p est premier différent de deux, l'ordre du groupe multiplicatif est toujours pair.

  • Structure de l'ensemble Q des résidus quadratiques de Fp* :
Soit φ l'endomorphisme de groupe de Fp* qui à x associe x2. Son noyau est composé des deux éléments 1 et -1. L'image d'un morphisme de groupe est toujours un sous-groupe. Cette image, par définition égal à l'ensemble des résidus quadratiques Q, est donc un sous-groupe. Le théorème de Lagrange montre que l'ordre de Q est égal à (p - 1 )/2, car 2 est l'ordre du noyau.
Soit ψ le morphisme canonique de Fp* dans Fp*/Q. C'est un morphisme dans un groupe à deux éléments dont le noyau est l'ensemble des résidus quadratique, ainsi a est un résidu quadratique si et seulement si ψ(a) = 1. Cette propriété montre que le produit a.b de deux éléments de Fp* est quadratique si a et b sont simultanément quadratiques ou si aucun des deux ne l'est.

Soit A l'ensemble des résidus quadratiques de Fp* différents de - 1 et B celui des résidus non quadratiques différents de - 1. On remarque que si b est un élément de B, alors b-1 est différent de b. En effet, les seuls éléments égaux à leurs inverses sont 1 et -1 et aucun élément de B n'est égal à l'un de ceux là. Le produit de b par b-1 est égal à 1 donc à un résidu quadratique, ce qui montre que b-1 n'est pas quadratique car b ne l'est pas non plus. En regroupant dans B les éléments avec leurs inverses, on remarque que l'ordre de B est nécessairement pair.

  • Caractère quadratique de -1 dans Fp* :
Comme p est impair, il est congru soit à 1, soit à 3 modulo 4. Supposons qu'il existe n tel que p - 1 = 4.n. Il existe exactement 2.n résidus quadratiques et donc aussi 2.n résidus non quadratiques. De plus, B est de cardinal pair tout comme l'ensemble des résidus non quadratiques. L'élément -1 est donc nécessairement quadratique.
Supposons qu'il existe n tel que p - 1 = 4.n + 2. Alors il existe exactement 2.n + 1 résidus non quadratiques. B est de cardinal pair, donc -1 est un résidu non quadratique, ce qui termine la démonstration.

Étudions à présent le polynôme formel P(X) de Fp[X] défini par :

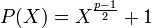
P(X) = X^{\frac{p-1}2} +1
  • Racines du polynôme P(X) :
Il admet au plus (p - 1)/2 racines. Le petit théorème de Fermat montre que tout résidu quadratique à la puissance (p - 1)/2 est égal à 1 et tout résidu non quadratique à la même puissance donne une valeur dont le carré est égal à 1 et qui est différent de 1. En conséquence tout résidu non quadratique à la puissance (p - 1)/2 est égal à -1. Et tout résidu non quadratique est racine de P(X). Comme le cardinal de Fp* - Q est exactement (p - 1)/2, on obtient l'égalité suivante :
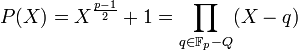
P(X) = X^{\frac{p-1}2} +1 = \prod_{q\in \mathbb F_p - Q}(X -q)

Considérons alors l'ensemble C égal à B + 1, c'est-à-dire l'ensemble des éléments de B auxquels on ajoute 1. L'égalité suivante montre que la moitié des éléments de C sont des résidus quadratiques et l'autre non :

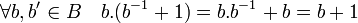
\forall b, b' \in B\quad b.(b^{-1}+1) = b.b^{-1} + b = b + 1

En effet, si b + 1 est un résidu quadratique, comme b ne l'est pas, b-1 - 1 ne l'est pas non plus. Inversement, si b + 1 n'est pas un résidu quadratique, comme b ne l'est pas, b-1 + 1 l'est nécessairement. Analysons p en fonction de son reste modulo 8. Soit n et r les deux entiers tel que p = 8.n + r, avec r élément de {1, 3, 5, 7}.

  • Caractère quadratique de 2 si r est égal à 1 ou 5 :
Si r est égal à 1 ou 5, alors p - 1 est un multiple de 4. En conséquence, -1 est un résidu quadratique et B est l'ensemble des non résidus quadratiques. Comme (p - 1)/2 est pair, le calcul de P(1) montre que :
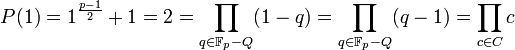
P(1) = 1^{\frac{p-1}2} +1=2=\prod_{q\in \mathbb F_p - Q}(1 -q)=\prod_{q\in \mathbb F_p - Q}(q-1)=\prod_{c\in C} c
Si r est égal à 1, le cardinal de C, égal à celui de B est égal à 4.n et C contient exactement 2.n résidus non quadratiques. Le produit de tous les éléments de C est donc quadratique, ce qui permet de conclure au caractère quadratique de 2. Si r est égal à 5, le cardinal de C est 4.n + 2 et C contient exactement 2n + 1 résidus non quadratiques. Le produit de tous les éléments de C est non quadratique, ce qui permet de conclure au caractère non quadratique de 2.
  • Caractère quadratique de 2 si r est égal à 3 ou 7 :
Pour ces cas, -1 n'est pas dans B et n'est pas un résidu quadratique. Le polynôme X + 1 divise P(X). Notons Q(X) le polynôme défini par :
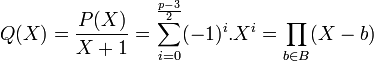
Q(X) = \frac {P(X)}{X+1}=\sum_{i=0}^{\frac {p-3}2}(-1)^i.X^i=\prod_{b\in B}(X - b)
Comme B est de cardinal pair, on obtient :
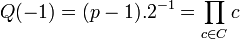
Q(-1)=(p-1).2^{-1}=\prod_{c\in C} c
L'élément p - 1 n'est pas un résidu quadratique dans ce cas, et l'inverse de 2 est un résidu quadratique si et seulement si 2 l'est. En conséquence, 2 est un résidu quadratique si le produit des éléments de C ne l'est pas et réciproquement.
C contient exactement 4.n +(r - 3)/2 éléments, donc si r est égal à 3, C contient 2.n résidus non quadratiques le produit des éléments de C est quadratique, donc 2 ne l'est pas. Si r est égal à 7, C contient 2.n + 1 résidus non quadratiques et le produit des éléments de C n'est pas quadratique, donc 2 l'est, ce qui termine l'analyse des différents cas.
 

Généralisations

Il existe des lois de réciprocité cubique, biquadratique (c'est-à-dire de degré 4) et ainsi de suite. Cependant la véritable généralisation de toutes ces lois, généralisation monumentale, est la théorie des corps de classes.

Le lemme de Gauss concerne les propriétés des résidus quadratiques et sert dans la démonstration établie par Gauss de la loi de réciprocité quadratique.

Liens externes

  • Portail des mathématiques Portail des mathématiques

Notes et références

Références

  1. ↑ Gauß, Eisenstein, and the ``third'' proof of the Quadratic Reciprocity Theorem: Ein kleines Schauspiel
  2. ↑ Cette démonstration fut publiée dans l'article : T. J. Stieltjes Sur le caractère quadratique de deux Annales de la faculté des sciences de Toulouse 1ière série Tome 11 N° 1 1897 p 5-8 lire
Ce document provient de « Loi de r%C3%A9ciprocit%C3%A9 quadratique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Loi de reciprocite quadratique de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Loi De Réciprocité Quadratique — En mathématiques, et plus précisément en théorie algébrique des nombres, la loi de réciprocité quadratique, conjecturée par Euler et Legendre et correctement démontrée pour la première fois par Gauss, établit un lien entre la résolubilité de deux …   Wikipédia en Français

  • Loi de réciprocité quadratique — En mathématiques, et plus précisément en théorie algébrique des nombres, la loi de réciprocité quadratique, conjecturée par Euler et Legendre et correctement démontrée pour la première fois par Gauss, établit un lien entre la résolubilité de deux …   Wikipédia en Français

  • Quadratique — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Quadratique », sur le Wiktionnaire (dictionnaire universel) Le terme de quadratique recouvre plusieurs …   Wikipédia en Français

  • réciprocité — [ resiprɔsite ] n. f. • 1729; bas lat. reciprocitas ♦ Caractère, état de ce qui est réciproque (I, 1o). La réciprocité d un sentiment d estime, d antipathie. À charge, à titre de réciprocité. Dr. internat. Traité de réciprocité (entre pays). ●… …   Encyclopédie Universelle

  • Corps Quadratique — Entier quadratique Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier quadratique est un nombre réel ou complexe racine d un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du …   Wikipédia en Français

  • Corps quadratique — Entier quadratique Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier quadratique est un nombre réel ou complexe racine d un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du …   Wikipédia en Français

  • Corps quadratique imaginaire — Entier quadratique Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier quadratique est un nombre réel ou complexe racine d un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du …   Wikipédia en Français

  • Entier quadratique — Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier quadratique est un nombre réel ou complexe, racine d un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du terme du plus… …   Wikipédia en Français

  • Irrationnel Quadratique — Entier quadratique Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier quadratique est un nombre réel ou complexe racine d un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du …   Wikipédia en Français

  • Irrationnel quadratique — Entier quadratique Pour les articles homonymes, voir Entier (homonymie). En mathématiques, un entier quadratique est un nombre réel ou complexe racine d un polynôme du second degré à coefficients dans les nombres entiers et dont le coefficient du …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”