- Loi de hubble
-
Loi de Hubble
 Pour les articles homonymes, voir Hubble.
Pour les articles homonymes, voir Hubble. Le télescope Hooker de l'observatoire du Mont Wilson, en Californie. Edwin Hubble a utilisé cet instrument pour découvrir la loi qui porte son nom.
Le télescope Hooker de l'observatoire du Mont Wilson, en Californie. Edwin Hubble a utilisé cet instrument pour découvrir la loi qui porte son nom.
En astronomie, la loi de Hubble énonce que les galaxies s'éloignent les unes des autres à une vitesse (approximativement, voir ci-dessous) proportionnelle à leur distance. Autrement dit, plus une galaxie est loin de nous, plus elle semble s'éloigner rapidement. Cette loi ne concerne bien évidemment que la partie de l'univers accessible aux observations (univers observable). L'extrapolation de la loi de Hubble sur des distances plus grandes est possible, mais uniquement si l'univers demeure homogène et isotrope sur de plus grandes distances.
Sommaire
Expansion de l'univers et mouvements propres
Il s'agit là d'un mouvement d'ensemble des galaxies de l'univers. À celui-ci se superposent les mouvements propres acquis par les galaxies du fait de leurs interactions gravitationnelles avec leurs voisines. Par exemple, la Voie lactée forme un système gravitationnellement lié avec la galaxie d'Andromède qui ont toutes deux une orbite elliptique très allongée qui fait qu'actuellement, la galaxie d'Andromède s'approche de nous. De même, la Voie lactée et la galaxie d'Andromède se rapprochent peu à peu du superamas de la Vierge. Néanmoins, au-delà d'une certaine distance, le mouvement général d'expansion l'emporte sur les mouvements propres, et toutes les galaxies lointaines s'éloignent de nous.
Genèse de la loi de Hubble
La loi de Hubble tire son nom de l'astronome américain Edwin Hubble qui la publia en 1929. Elle fut la première preuve de l'expansion de l'univers, un phénomène générique prédit par la relativité générale, et du Big Bang, le modèle cosmologique qui en résulte le plus naturellement. Hubble découvrit cette loi en observant un décalage vers le rouge presque systématique dans les galaxies dont il avait découvert auparavant la nature exacte à l'aide de l'observation d'un certain type d'étoiles variables, les céphéides. Ces étoiles sont sujettes à des variations de luminosité dont la période est reliée à la luminosité absolue suivant une loi établie par l'astronome Henrietta Leavitt au début du XXe siècle. L'observation de la période de variation des céphéides dans une autre galaxie permettait ainsi de déduire leur distance relative. La vitesse de fuite de ces mêmes galaxies était, elle, mesurée par l'observation d'un décalage vers le rouge de leur spectre, effet interprété comme étant dû à leur mouvement de fuite (voir effet Doppler-Fizeau).
C'est en comparant ce décalage à la distance de ces galaxies, qu'il trouva une relation linéaire entre les deux, annoncée en 1929[1]. Pour cette raison, la paternité de la loi de Hubble est attribuée à Edwin Hubble, d'où son nom. Cependant, deux ans plus tôt, Georges Lemaître avait prédit l'existence de cette loi en étudiant un type de modèle issu de la relativité générale. Dans son article écrit en français et publié dans les Annales de la société scientifique de Bruxelles, il indique clairement que cette loi qu'il a prédite est vérifiée par les observations dont il dispose (pour la plupart œuvres de Hubble et Gustaf Strömberg)[2]. Étant publié en français, et traduit en anglais par Arthur Eddington après la publication des résultats de Hubble (en 1931), ce résultat de Lemaître est resté inaperçu, d'autant que la traduction anglaise de son article par Eddington est étrangement amputée de la phrase clé qui énonce la relation[3].
Formule de la loi de Hubble
La vitesse de récession apparente v des galaxies étant déduite de la formule Doppler et sa distance d mesurée par les céphéides, la loi de Hubble s'écrit simplement
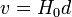 ,
,
où H0 est la constante de Hubble, la lettre H étant bien sûr utilisée en l'honneur de Hubble. L'indice 0 est utilisé pour indiquer la valeur de la constante à l'instant présent. Celle-ci en effet n'est pas constante dans le temps. Elle était plus élevée par le passé (bien que certaines observations semblent indiquer qu'elle serait en augmentation depuis quelques milliards d'années).
On peut le cas échéant remplacer la vitesse v par sa valeur déduite du décalage vers le rouge z et la vitesse de la lumière c pour obtenir
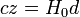 .
.
Ces deux lois ne sont valables que pour de faibles valeurs de la vitesse, donc pour des distances relativement faibles. On sait de nos jours que l'interprétation du décalage vers le rouge en termes d'effet Doppler n'est pas correcte physiquement puisque l'augmentation de distance au cours du temps entre deux galaxies n'est pas due à la vitesse des galaxies dans un espace fixe mais plutôt à un étirement de l'espace lui-même, les galaxies restant fixes dans cet espace. Il faut donc faire une analyse différente. On trouvera plus loin des détails sur l'interprétation physique de la loi de Hubble et les modifications à la loi de Hubble qui en résultent.
Interprétation physique de la loi de Hubble
Article détaillé : Expansion de l'univers.Si l'on se restreint à l'application de la loi de Hubble dans l'univers local (quelques centaines de millions d'années lumière), alors il est tout à fait possible d'interpréter la loi de Hubble comme un mouvement des galaxies dans l'espace. Néanmoins, la loi énonçant une vitesse de récession apparente proportionnelle à la distance, son extrapolation conduit à conclure que des galaxies suffisamment lointaines s'éloignent de nous à une vitesse plus grande que la vitesse de la lumière, en contradiction apparente avec la relativité restreinte. De fait, ce n'est pas dans le cadre de la relativité restreinte que l'on doit appliquer la loi de Hubble, mais celui de la relativité générale. Celle-ci stipule entre autres que le concept de vitesse relative entre deux objets (deux galaxies distantes, par exemple), est un concept purement local : on ne peut mesurer la différence de vitesse entre deux objets que si leur trajectoires sont « suffisamment proches » l'une de l'autre. Il convient bien sûr de préciser ce dernier terme, qui en l'occurrence dit essentiellement que la notion de vitesse relative n'a de sens que dans une région de l'espace-temps qui peut être correctement décrite par une métrique de Minkowski. Il est en effet possible de montrer (voir Expansion de l'univers) que l'échelle de longueur au-delà de laquelle on ne peut plus décrire localement un espace en expansion par une métrique de Minkowski est précisément le rayon de Hubble, soit la distance au-delà de laquelle les vitesses de récession apparentes sont précisément relativistes.
L'interprétation en termes de mouvement dans l'espace décrit par la relativité restreinte devient donc précisément invalide au moment où surgit le paradoxe d'une vitesse de récession supérieure à la vitesse de la lumière. Ce paradoxe est résolu dans le cadre de la relativité générale qui permet d'interpréter la loi de Hubble non pas comme un mouvement dans l'espace, mais une expansion de l'espace lui-même. Dans ce cadre-là, le postulat d'impossibilité de dépassement de la vitesse de la lumière fréquemment (et improprement) employé en relativité restreinte se reformule de façon plus exacte en énonçant qu'aucun signal ne peut se déplacer à une vitesse supérieure à celle de la lumière, les vitesses étant localement mesurées par des observateurs dans des régions où l'espace peut être décrit par la relativité restreinte (soit à petite échelle).
Valeur de la constante de Hubble
Article détaillé : Constante de Hubble.La valeur actuelle de la constante de Hubble est aujourd'hui (2006) mesurée à 72 kilomètres par seconde et par mégaparsec, avec une incertitude d'environ 10 % (8 kilomètres par seconde et par mégaparsec)[4]. Ce résultat est obtenu de façon consistante par de nombreuses méthodes :
- La méthode historique de Hubble à l'aide de céphéides ;
- Des méthodes similaires basées sur l'utilisation de supernovae de type Ia et de type II ;
- L'étude du plan fondamental des galaxies ;
- L'étude des décalages des fluctuations de luminosité des images multiples des quasars dont plusieurs images sont produites par des effets de lentille gravitationnelle.
La valeur actuelle est considérablement plus basse que la valeur initiale trouvée par Hubble (de l'ordre de 500 km s-1 Mpc-1). L'erreur commise par Hubble était due à une mauvaise estimation de la magnitude absolue des céphéides, aujourd'hui considérablement mieux connue (voir mesure des distances en astronomie).
Modifications à la loi de Hubble
Tant que l'on considère des galaxies dont la vitesse de récession est faible, leur distance à un observateur varie peu entre le moment où elles émettent leur lumière et le moment où celle-ci est reçue par l'observateur. De même tant que le temps de propagation du signal lumineux est petit devant le temps caractéristique de l'expansion, le temps de Hubble la vitesse de récession et le taux d'expansion varient peu sur cet intervalle. Ainsi, il n'y a pas d'ambiguïté dans la définition des quantité v, H0, et d. À grande distance, il convient de préciser ce que l'on entend par distance, et vitesse de récession. De plus, rien ne garantit a priori que la relation linéaire mentionnée plus haut reste valable. Il existe en fait des corrections à la loi de Hubble. Celles-ci jouent un rôle crucial en cosmologie car elles permettent en principe de reconstituer directement l'histoire récente de l'expansion.
Si l'on appelle d la distance qui nous sépare actuellement de la galaxie observé, on peut montrer que pour des décalages vers le rouge modérés, ces deux quantités sont reliées par la formule[5]
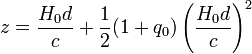 ,
,
où la quantité q0 est le paramètre de décélération de l'expansion, proportionnelle à la dérivée seconde du facteur d'échelle.
DémonstrationLa métrique considérée étant de type Friedmann-Lemaître-Robertson-Walker, l'élément de longueur s'écrit, en supposant la courbure spatiale nulle,
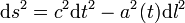 ,
,
où dl2 représente l'élément de longueur en coordonnées comobiles, par rapport auxquelles les galaxies ont un mouvement négligeable. Cette relation peut se réécrire en introduisant le temps conforme η en :
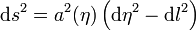 .
.
Un photon est une particule de genre lumière, sa propagation se fait selon
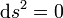 ,
,
ce qui s'écrit immédiatement :
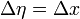 ,
,
c'est-à-dire que la distance en coordonnées comobile de la galaxie est exactement égale à l'intervalle en temps conforme. La distance physique se déduisant de la distance comobile par la formule
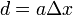 ,
,
la distance de la galaxie peut s'écrire
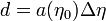 ,
,
où l'on précise que le facteur d'échelle aujourd'hui est évalué à la valeur actuelle du temps conforme, η0. De plus, le facteur d'échelle aeau moment de l'émission de la lumière de la galaxie est relié à la valeur actuelle a0 et au redshift par la formule
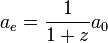 ,
,
mais cette formule correspond aussi à la valeur du facteur d'échelle à l'époque où le temps conforme valait η0 − Δη. On a donc
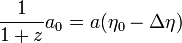 .
.
Il suffit désormais d'effectuer un développement limité de cette expression. On pose
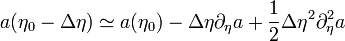 .
.
D'après la définition du temps conforme, les dérivée par rapport à celui-ci se relient à celles par rapport au temps cosmique t par
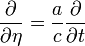 .
.
En utilisant l'expression ci-dessus, il vient :
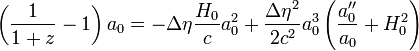 .
.
En introduisant le paramètre de décélération q0 défini par
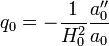 ,
,
il vient
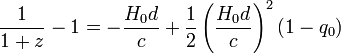 .
.
En développant le terme de gauche en z et en ne gardant que les termes d'ordre 2 en z et en d, on trouve finalement
Cette relation est importante car elle permet de mesurer le paramètre de décélération et par suite déduire la pression moyenne des différentes formes de matière qui composent l'univers.
En pratique, la quantité d n'est pas mesurable directement. Ce que l'on mesure, c'est soit la distance obtenue en comparant la luminosité apparente d'un astre à sa luminosité intrinsèque supposée connue, dL (on parle alors de distance de luminosité), soit la distance obtenu en mesurant son diamètre apparent, sa taille réelle étant dans ce cas supposée connue, dA(on parle alors de distance angulaire). Dans ce cas, on exprime généralement les distances en fonction du redshift et non le contraire, et les formules s'écrivent :
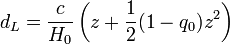 ,
,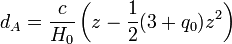 .
.
DémonstrationEn l'absence de courbure spatiale, ces deux distances se déduisent de d par les formules
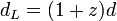 ,
,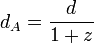 .
.
En remplaçant d par l'une ou l'autre de ces expression dans la formule trouvée précédemment, on trouve immédiatement les résultats énoncés.
En pratique pour des objets lointains, on n'utilise pas les formules ci-dessus, qui ne sont valides que pour des petits décalages vers le rouge. Voir les articles distance angulaire et distance de luminosité pour plus de détails.
Autres hypothèses proposées
Des réticences, initiées par Albert Einstein lui-même du fait de sa préférence pour un univers statique (voir univers d'Einstein), ont été formulées vis-à-vis de l'interprétation du décalage vers le rouge en termes de fuite des galaxies ou d'expansion de l'espace. Aucune des alternatives proposées n'est considérée comme viable aujourd'hui, en raison du manque de motivations théoriques sous-jacentes (il s'agit essentiellement de phénomènes ad hoc invoqués uniquement pour réinterpréter ces résultats, comme la lumière fatiguée) et qui échouent à proposer un modèle cosmologique rendant compte de l'ensemble des observations désormais disponibles (voir l'article expansion de l'univers). Par exemple, la théorie de la lumière fatiguée échoue à expliquer le fait que le fond diffus cosmologique a un spectre de type corps noir.
Références
- Jean-Pierre Luminet, L'invention du Big Bang, Seuil, coll. « Points Sciences » (2004) (ISBN 2020611481). En particulier pages 102 et 108.
Notes
- ↑ (en) Edwin Hubble, A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae, Proceedings of the National Academy of Sciences of the United States of America, 15, 168-173 (1929) Lire en ligne
- ↑ Georges Lemaître, Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extragalactiques, Annales de la société scientifique de Bruxelles A47, 49-59 (1927)
- ↑ (en) Georges Lemaître, Expansion of the universe, A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulae, Monthly Notices of the Royal Astronomical Society, 91 483-490 (1931) Lire en ligne
- ↑ (en) Wendy L. Freedman et al., Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant, Astrophysical Journal, 553, 47-72 (2001) Lire en ligne
- ↑ Voir par exemple (en) Jochen Weller, Dark Energy — Observational Evidence and Theoretical Modeling, Lectures I+II, p. 12-13
Voir aussi
Articles connexes
- Céphéide
- Constante de Hubble
- Distance angulaire
- Distance de luminosité
- Edwin Hubble
- Effet Doppler-Fizeau
- Expansion de l'univers
- Mesure des distances en astronomie
- Modèle standard de la cosmologie
- Paramètre de décélération
- Portail de la cosmologie
- Portail de l’astronomie
Catégorie : Cosmologie
Wikimedia Foundation. 2010.
