Loi de hotelling

A ne pas confondre avec la Rente d'Hotelling.

La loi de Hotelling affirme que sur la plupart des marchés, la rationalité conduit les producteurs à réduire la différence entre leurs produits. Cette loi est aussi appelée principe de différentiation minimale. Elle a été formulée par le statisticien et économiste américain Harold Hotelling (1895-1973)^[1]. Le phénomène inverse est la différenciation des produits, généralement considérée comme un avantage commercial si elle s'effectue dans les bonnes conditions.

Il s'agit d'une première approche pour les problèmes de différentiation spatiale en utilisant la géométrie. Le modèle de Hotelling aussi appelé modèle de la ville linéaire est étendu par le modèle de Salop dit de la ville circulaire qui considère non plus une droite, mais un cercle-unité. Alors que la droite permet de modéliser une autoroute, le cercle modélise plus facilement une ville autour d'un lac ou une périphérie urbaine.

Sommaire 1 Exemple 2 Le modèle 3 Application 4 Notes 5 Bibliographie

Exemple

Supposons que deux magasins concurrents s'installent dans une même rue orientée nord-sud. Chaque magasin va chercher une implantation lui permettant de maximiser ses parts de marché en attirant à lui le plus grand nombre de consommateurs possible (dans cet exemple, c'est le magasin qui joue le rôle du « produit » évoqué dans la loi de Hotelling). Les consommateurs sont uniformément répartis tout au long de la rue. Supposons également que chaque consommateur se dirige toujours vers le magasin le plus proche.

Pour un magasin unique, l'implantation optimale est exactement à mi-rue, à égale distance des deux extrémités de l'axe. D'un point de vue strictement économique (celui du propriétaire du magasin), le magasin peut se trouver n'importe où puisqu'en raison de sa situation de monopole, les consommateurs iront obligatoirement vers lui. D'un point de vue social (celui du consommateur), implanter le magasin au milieu de l'axe permet de minimiser (en moyenne) les déplacements des consommateurs. La loi de Hotelling prévoit que si deux magasins sont en concurrence pour s'installer dans une même rue, alors ils s'installeront plutôt vers le milieu de l'axe. L'un attirera les consommateurs situés sur le tronçon nord, l'autre les consommateurs situé sur le tronçon sud.

Il est évident que d'un point de vue social, il serait plus avantageux que les deux magasins ne soient pas côte à côte mais plutôt décalés chacun d'un quart de la longueur disponible vers chaque extrémité de l'axe. Chacun des magasins drainerait toujours une moitié du marché (la moitié nord pour le magasin implanté au milieu du tronçon nord, la moitié sud pour celui implanté au milieu du tronçon sud) et les consommateurs auraient en moyenne moins de distance à parcourir pour s'approvisionner. Pourtant, aucun des deux propriétaires ne prendra spontanément cette initiative puisque cela permettrait à l'autre magasin de s'implanter au milieu de la rue et de s'approprier plus de la moitié du marché.

Ce phénomène est observé sur de nombreux marchés, en particulier sur ceux des marchandises (par opposition aux services) et a pour conséquence une diminution de la variété des choix disponibles pour le consommateur.

Le modèle

Hotelling prend le cas de deux magasins (A et B) qui se trouvent sur une route rectiligne de longueur L. A se trouve à a kilomètres du début de la route et B se trouve à b kilomètres avant la fin de la route :

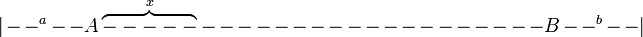
Le bien vendu est homogène et le prix de revient est de u $ par unité. Les consommateurs sont distribués uniformément le long de la route à raison d’un consommateur par kilomètre. Chaque consommateur achète une unité du bien. Son choix du magasin dépend du prix de vente et du coût de transport qui est de c $ par kilomètre. Il s’agit donc d’un cas de duopole avec biens différenciés car les frais de transport rendent les deux biens différents.

Si les prix étaient les mêmes, A aurait les consommateurs à gauche (a) et la moitié des consommateurs entre A et B. Dans le cas général, la répartition des consommateurs dépendra des prix fixés par A et B.

Soit x la distance entre A et un consommateur qui se trouve entre A et B (voir graphique). Si d est la distance entre A et B, le consommateur est indifférent entre aller chez A ou chez B lorsque :

p_A + cx = p_B + c(d − x)

où 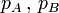sont les prix de vente respectifs pratiqués par les deux magasins et 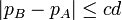. On obtient :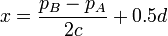

Les profits des deux magasins seront alors:

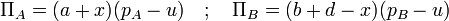
L’équilibre de Cournot-Nash est obtenu en utilisant les deux courbes de réaction (ou de meilleure réponse) :

Le point de rencontre de ces deux courbes donne la solution (Hotelling suppose que u=0, comme Cournot avec l’eau minérale):

Hotelling constate que le profit de A augmente s’il se rapproche de B (c’est-à-dire lorsque a augmente). Les deux entreprises ont alors intérêt à se rapprocher. Hotelling suggère que ce résultat peut expliquer aussi la standardisation des produits ou des programmes des partis politiques aux États-Unis (différence entre Républicains et Démocrates).

Il ne faut pas que les deux magasins soient trop proches l’un de l’autre car alors on est dans le cas du modèle de Bertrand avec un prix d’équilibre égal au coût unitaire et un profit nul. Si a=b et L > 2a, alors A ne peut pas dépasser le premier quart de la route. Si, comme dans l’exemple de Hotelling, b=1 et L=35, alors A peut aller jusqu’à environ 10 Km. Il ne doit pas aller jusqu’au milieu de la route.

Si les coûts de transport sont quadratiques, A a intérêt à s’éloigner de B (différenciation des produits).

Application

Dans les faits, les entreprises sont soumises à la fois à la loi de Hotelling et au principe opposé de différenciation des produits. Ainsi, une nouvelle compagnie d'aviation fera-t-elle sa promotion en insistant sur ce qui la différencie de la concurrence : trajets moins onéreux, places plus confortables, etc. Mais elle adoptera également une politique très proche de celle de ses concurrents : services et grilles horaires similaires.

Notes

Bibliographie

• C. d’Aspremont, J.J. Gabszewicz, J.F. Thisse, “On Hotelling’s ‘Stability in Competition’”, Econometrica, 1979, pp. 1145-1150
• Harold Hotelling, « Stability in Competition », Economic Journal, vol. xxxix (1929), 41-57.

• Portail de l’économie