- Formule de stirling
-
Formule de Stirling
 Pour les articles homonymes, voir Stirling.
Pour les articles homonymes, voir Stirling.La formule de Stirling, du nom du mathématicien James Stirling, donne un équivalent de la factorielle au voisinage de l'infini réel (quand n tend vers l'infini) :
que l'on trouve souvent écrit ainsi :
Sommaire
Version continue
La formule précédente est un cas particulier, pour un argument entier, de la formule asymptotique de Stirling pour la fonction Γ d'Euler.
Histoire
La formule a d'abord été découverte par Abraham de Moivre sous la forme
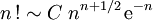 ,
,
- où C est une constante réelle (non nulle).
L'apport de Stirling[1] fut de donner un développement de ln(n!) à tout ordre et d'attribuer la valeur
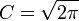 à la constante. La démonstration classique de ceci est donné dans l'article intégrales de Wallis.Démonstration du résultat de Moivre
à la constante. La démonstration classique de ceci est donné dans l'article intégrales de Wallis.Démonstration du résultat de MoivreLa détermination de la constante n'est pas immédiate, mais il est facile de montrer le résultat de Moivre. En effet, en posant
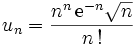 , il suffit de montrer que la suite (un) converge, et que sa limite est non nulle. Or (un) étant à termes strictement positifs pour
, il suffit de montrer que la suite (un) converge, et que sa limite est non nulle. Or (un) étant à termes strictement positifs pour 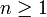 , on peut définir :
, on peut définir :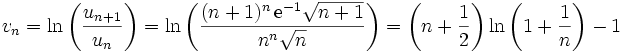
de telle sorte qu'en utilisant le développement limité de ln(1 + x) en 0 à l'ordre 3, on obtient :
![v_n = \left(n+ \frac{1}{2}\right)\left[\frac{1}{n}-\frac{1}{2n^2}+\frac{1}{3n^3}+ o\left(\frac{1}{n^3}\right) \right] -1 = 1-\frac{1}{2n}+ \frac{1}{3n^2}+ O\left(\frac{1}{n^2}\right)+\frac{1}{2n}-\frac{1}{4n^2}+O\left(\frac{1}{n^3}\right)-1 = \frac{1}{12n^2}+O\left(\frac{1}{n^2}\right)](/pictures/frwiki/102/fc73b7d29a35f80201e9f652876e00a3.png)
On en déduit que
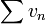 est une série absolument convergente, donc en écrivant vn sous la forme : vn = ln(un + 1) − ln(un), on trouve que la suite (ln(un)) converge (vers une limite que nous notons L), donc la suite (un) aussi, et vers la limite non nulle exp(L), ce qu'on voulait démontrer.
est une série absolument convergente, donc en écrivant vn sous la forme : vn = ln(un + 1) − ln(un), on trouve que la suite (ln(un)) converge (vers une limite que nous notons L), donc la suite (un) aussi, et vers la limite non nulle exp(L), ce qu'on voulait démontrer.- pour introduire le facteur de deMoivre, une autre manière de présenter est la suivante : la formule d'Euler-Maclaurin appliquée à la fonction ln x entre 1 et n donne ln n! = sigma ( ln k ) = somme ( ln x), de x=1 à x= n) + 1/2 . ln 1 + 1/2. ln n +reste(n) .
Soit, ln (n!) = n.ln(n) - n +1 + 1/2. ln(n) +petitreste(n). On prend alors l'exponentielle et cela donne l'idée du calcul ci-dessus.
-
- On peut même introduire le facteur sqrt( 2.Pi) par la méthode de la descente-rapide ( appelée aussi méthode du col). Cette méthode est assez puissante et en l'appliquant, on "comprend" l'apparition du sqrt(2.Pi) et on trouve immédiatement le résultat de Stirling.
Généralisation
On peut améliorer la qualité de l'approximation de Stirling en utilisant le développement asymptotique de la fonction gamma Γ ; on trouve :
En fait, Abraham de Moivre généralisa le résultat de Stirling sous la forme
![\ln [n!] = (n+\frac12)\ln(n)-n + \ln(2\pi)+\sum_{k\ge 1}\frac{B_{2k}}{2k(2k-1)n^{2k-1}},](/pictures/frwiki/51/30ad48da470f8522bc6cf3e41de277f8.png)
où les nombres B2k sont les nombres de Bernoulli. Écrite sous la forme
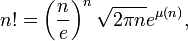
on trouve la formule (et la fonction) de Binet.
La formule d'Euler-MacLaurin permet d'aboutir au résultat à l'ordre que l'on veut.
(Sloane's A001163 and A001164).
Calculs numériques
Pour juger de sa précision, on peut faire le tableau des premières valeurs de n
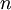
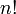
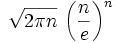
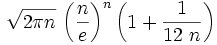
1
2
3
4
5
6
7
8
9
10
15
20
25
30
401
2
6
24
120
720
5 040
40 320
362 880
3 628 800
1 307 674 368 000
2 432 902 008 176 640 000
15 511 210 043 330 985 984 000 000
265 252 859 812 191 058 636 308 480 000 000
815 915 283 247 897 734 345 611 269 596 115 894 272 000 000 0000,93
1,92
5,84
23,51
118,02
710,08
4 980,4
39 902,4
359 536,9
3,598 696 x 106
1,300 431 x 1012
2,422 787 x 1018
1,545 959 x 1025
2,645 171 x 1032
8,142 173 x 10470,999
1,999
5,998
23,996
119,99
719,94
5 039,7
40 318,1
362 866,0
3,628 685 x 106
1,307 665 x 1012
2,432 882 x 1018
1,551 113 x 1025
2,652 519 x 1032
8,159 136 x 1047- faire attention : tableau à regarder en plein écran, sinon réajuster.
- Note : dans la sqrt(n), si on remplace n par n+1/6 les calculs sont nettement améliorés, pour les petites valeurs de n (approximation de Gosper); on peut aussi préférer un encadrement : cf Wolfram ; enfin on peut prendre la suite Sloane A 055 775.
Notes et références
- ↑ Jacobo Stirling, Methodus Differentialis sive Tractatus de Summatione et Interpolatione Serierum Infinitarum, (1730), proposition 28, p.135
- Portail des mathématiques
Catégorie : Analyse réelle
Wikimedia Foundation. 2010.

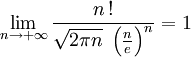
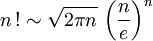
![n\,! = \sqrt{2\pi n}\,\left({n \over e}\right)^n \left[1 + \frac{1}{12\ n} + \frac{1}{288\ n^2} - \frac{139}{51\ 840\ n^3} - \frac{571}{2\ 488\ 320\ n^4} + \frac {163\ 879}{209\ 018\ 880\ n^5} + \mathcal{O} \left(\frac{1}{n^6} \right) \right]](/pictures/frwiki/100/d5b98e78ef255c3da0de81e51570e77c.png)