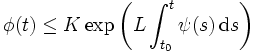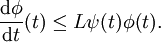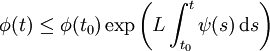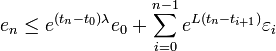Inégalité de Grönwall

Inégalité de Grönwall

Lemme de Grönwall

En mathématiques, le lemme de Grönwall, nommé d'après Thomas Hakon Grönwall (1877-1932) qui l'établit en 1919, permet l'estimation d'une fonction qui vérifie une certaine inégalité différentielle. Le lemme existe sous deux formes, intégrale et différentielle.

Le lemme de Grönwall constitue la justification et l'outil d'obtention de nombreuses approximations des solutions d'équations différentielles ordinaires. En particulier, il est utilisé pour démontrer l'unicité d'une solution au problème de Cauchy, au travers du théorème de Cauchy-Lipschitz.

Sommaire

Forme intégrale

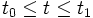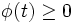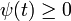Si, pour t_0\leq t\leq t_1, \phi(t)\geq 0 et \psi(t)\geq 0 sont des fonctions continues qui vérifient :

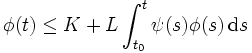\phi(t)\leq K+L\int_{t_0}^t \psi(s)\phi(s) \, \mathrm{d} s ,

où K et L sont des constantes positives, alors :

\phi(t)\leq K\exp\left(L\int_{t_0}^t \psi(s)\, \mathrm{d} s\right)

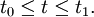
pour t_0\leq t\leq t_1.

Le principe de démonstration est le suivant: il s'agit de voir qu'en t0, on a égalité entre les deux majorants, puis, en dérivant le rapport 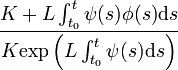\frac{K+L\int_{t_0}^t\psi(s)\phi(s)\mathrm{d}s}{K\mathrm{exp}\left(L\int_{t_0}^t \psi(s)\mathrm{d}s\right)}, voir que ce rapport est décroissant, ce qui prouve le résultat.

Forme différentielle

Si la relation suivante est vérifiée :

\frac{\mathrm{d} \phi}{\mathrm{d} t} (t) \leq L \psi(t) \phi (t).

Alors on a l'inégalité :

\phi(t)\leq K+L\int_{t_0}^t \psi(s)\phi(s) \, \mathrm{d} s


Ce qui permet de conclure que

\phi(t)\leq \phi(t_0) \exp\left(L\int_{t_0}^t \psi(s)\, \mathrm{d} s\right)

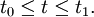
pour t_0 \leq t \leq t_1.

Forme discrète

La version discrète du lemme de Grönwall se présente dans la littérature en une multitude de déclinaisons. Elle est couramment utilisée pour étudier la stabilité numérique des schémas d'intégration.

Considérons les trois suites de nombres réels positifs suivantes :

Δtn le pas de temps à chaque itération,
en l'erreur totale (accumulée) à l'itération n,
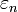\varepsilon _n l'erreur supplémentaire contribuée par l'itération n.

Considérons de plus le nombre réel positif λ qui représente un facteur d'amplification de l'erreur.

Finalement ajoutons pour simplifier l'écriture :

tn le temps à l'itération n,

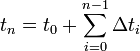de sorte que t_n=t_0+\sum_{i=0}^{n-1}\Delta t_i .

Si de plus les erreurs successives sont liées par la relation suivante :

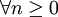
\forall n \geq 0

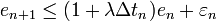e_{n+1}\leq(1+\lambda \Delta t_n)e_n+\varepsilon _n,

alors on a:

e_n \leq e^{(t_n - t_0)\lambda}e_0+\sum_{i=0}^{n-1}e^{L(t_n-t_{i+1})}\varepsilon _i

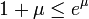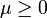La démonstration se fait par récurrence en notant que 1+\mu\leq e^{\mu} pour tout \mu\geq0.


Voir aussi

Liens externes

http://jipam.vu.edu.au/article.php?sid=125

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Lemme de Gr%C3%B6nwall ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Inégalité de Grönwall de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Lemme de Grönwall — En mathématiques, le lemme de Grönwall, nommé d après Thomas Hakon Grönwall (en) qui l établit en 1919, permet l estimation d une fonction qui vérifie une certaine inégalité différentielle. Le lemme existe sous deux formes, intégrale et… …   Wikipédia en Français

  • Lemme De Grönwall — En mathématiques, le lemme de Grönwall, nommé d après Thomas Hakon Grönwall (1877 1932) qui l établit en 1919, permet l estimation d une fonction qui vérifie une certaine inégalité différentielle. Le lemme existe sous deux formes, intégrale et… …   Wikipédia en Français

  • Lemme de Gronwall — Lemme de Grönwall En mathématiques, le lemme de Grönwall, nommé d après Thomas Hakon Grönwall (1877 1932) qui l établit en 1919, permet l estimation d une fonction qui vérifie une certaine inégalité différentielle. Le lemme existe sous deux… …   Wikipédia en Français

  • Lemme de grönwall — En mathématiques, le lemme de Grönwall, nommé d après Thomas Hakon Grönwall (1877 1932) qui l établit en 1919, permet l estimation d une fonction qui vérifie une certaine inégalité différentielle. Le lemme existe sous deux formes, intégrale et… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Somme des diviseurs — En arithmétique, la somme des diviseurs d un nombre entier strictement positif est l entier obtenu en effectuant la somme de tous les diviseurs positifs de cet entier. La fonction qui, à l entier n, associe la somme de ses diviseurs est souvent… …   Wikipédia en Français

  • Liste de théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”