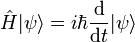- Inégalité de Heisenberg
-
Principe d'incertitude
 Vues spatiale (position) et fréquentielle (impulsion) de (a) une onde, (b) un paquet d'onde et (c) un corpuscule.L'onde étant de fréquence pure, son impulsion est définie mais elle n'est pas localisée dans l'espace. Inversement, le corpuscule est localisé mais n'a pas de fréquence déterminée. Le cas général est celui du paquet d'onde qui est distribué en fréquence comme en espace. Du fait de la dualité entre les deux représentations l'étalement spatial est inversement proportionnel à l'étalement fréquentiel.
Vues spatiale (position) et fréquentielle (impulsion) de (a) une onde, (b) un paquet d'onde et (c) un corpuscule.L'onde étant de fréquence pure, son impulsion est définie mais elle n'est pas localisée dans l'espace. Inversement, le corpuscule est localisé mais n'a pas de fréquence déterminée. Le cas général est celui du paquet d'onde qui est distribué en fréquence comme en espace. Du fait de la dualité entre les deux représentations l'étalement spatial est inversement proportionnel à l'étalement fréquentiel.
Le principe d'incertitude fut énoncé au printemps 1927 par Heisenberg lors des balbutiements de la mécanique quantique.
Le terme "incertitude" est le terme historique pour ce principe. Le nom de Théorème d'indétermination est parfois préféré car le principe ne porte pas sur l'ignorance par l'expérimentateur de grandeurs, mais bien sur l'impossibilité de les déterminer, et même d'affirmer qu'une détermination plus précise existe. De plus, ce principe étant prouvé par les équations, il devient un théorème.
Les travaux de Planck, Einstein et De Broglie avaient mis à jour que la nature quantique de la matière entraînait l'équivalence entre des propriétés ondulatoires (fréquence et vecteur d'onde) et corpusculaires (énergie et impulsion) selon les lois :
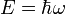 et
et 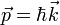 .
.La dualité onde-corpuscule confirmée alors par de nombreuses expérimentations posait un problème de fond aux physiciens. En effet, pour posséder une fréquence et un vecteur d'onde, un objet doit avoir une certaine extension en espace et en temps. Un objet quantique ne peut donc être ni parfaitement localisé, ni avoir une énergie parfaitement définie.
De manière simplifiée, ce principe d'indétermination énonce donc que — de façon assez contre-intuitive du point de vue de la mécanique classique — pour une particule massive donnée, on ne peut pas connaître simultanément sa position et sa vitesse. Soit on peut connaître précisément sa position (par ex: à ± 1 mm) contre une grande incertitude sur la valeur de sa vitesse (par ex: à ± 100 m/s), soit on peut connaître précisément sa vitesse (par ex: à ± 0,0001 m/s) contre une grande incertitude sur la valeur de sa position (par ex: à ± 1 km).
Cependant, si on renonce à considérer la particule en tant qu'objet corpusculaire, l'énoncé de ce principe devient plus intuitif. L'objet quantique ayant une certaine extension dans l'espace et une certaine durée de vie en temps, on le représente alors, non plus par un ensemble de valeurs scalaires (position, vitesse), mais par une fonction décrivant sa distribution spatiale. Toute l'information relative à la particule est contenue dans cette fonction d'onde. Les mesures scalaires effectuées sur cette particule consistent à extraire seulement une partie de cette information, par l'intermédiaire d'opérateurs mathématiques.
Sommaire
Historique du terme
Le principe d'incertitude est souvent appelé principe d'indétermination. L'emploi de ces deux termes pour désigner la même notion résulte d'un problème lors de la traduction en anglais de l'article de Heisenberg. En effet, lors de la première rédaction de son article, Heisenberg emploie les termes Unsicherheit (incertitude) et Ungenauigkeit (imprécision), puis, comprenant que ces termes peuvent prêter à confusion, il décide d'utiliser finalement le terme Unbestimmtheit (indétermination). Mais l'article est déja traduit et c'est le terme "principe d'incertitude" qui sera consacré.[1]
Bien que la dénomination « principe d'incertitude » soit la plus usitée, on devrait en toute rigueur parler de « principe d'indétermination ». Cependant l'expression s'est répandue à tel point qu'elle est aujourd'hui acceptée par tous les physiciens. Le terme de « principe » est aussi inapproprié, quoique souvent encore usité. Il conviendrait de parler de relations d'incertitude ou mieux de relations d'indétermination.En raison de ces connotations philosophiques, aujourd'hui les physiciens parlent des relations d'incertitude, ou des inégalités de Heisenberg, car il s'agit d'une inégalité portant sur des grandeurs physiques non-commutatives.
Les relations de Heisenberg
Considérons une particule massive non relativiste se déplaçant sur un axe.
Description classique
La mécanique classique de Newton affirme que la dynamique de la particule est entièrement déterminée si l'on connaît à chaque instant : sa position x et sa quantité de mouvement p = mv (également appelée : impulsion). Ces deux grandeurs physiques réelles ont des valeurs appartenant à
 , variant de -∞ à +∞. On dit que le couple (x,p) définit l'espace des phases de la particule. Toute grandeur physique est représentable par une fonction f (x,p) réelle. Cette théorie est conforme à la logique aristotélicienne, incluant la notion de tiers exclu : « il faut qu'une porte soit ouverte ou bien fermée. » Du point de vue mathématique, on décrit l'état de la particule par un nombre fini de grandeurs scalaires.
, variant de -∞ à +∞. On dit que le couple (x,p) définit l'espace des phases de la particule. Toute grandeur physique est représentable par une fonction f (x,p) réelle. Cette théorie est conforme à la logique aristotélicienne, incluant la notion de tiers exclu : « il faut qu'une porte soit ouverte ou bien fermée. » Du point de vue mathématique, on décrit l'état de la particule par un nombre fini de grandeurs scalaires.Description quantique
En mécanique quantique, la valeur précise des paramètres physiques tels que la position ou la vitesse n'est pas déterminée tant qu'elle n'est pas mesurée. Seule la distribution statistique de ces valeurs est parfaitement déterminée à tout instant. Cela peut mener au point de vue (qui est un abus de langage) selon lequel un objet quantique pourrait être "à plusieurs endroits en même temps". Un point de vue plus juste serait de dire que l'objet quantique n'a pas de localisation tant que la position n'est pas mesurée.
Cela dit, le paradoxe n'est qu'apparent. Il vient du fait que les grandeurs scalaires classiques sont insuffisantes pour décrire la réalité quantique. On doit faire appel à des fonctions d'onde qui sont des vecteurs appartenant à un espace de Hilbert de dimension infinie.
Les grandeurs classiques ne sont donc en fait que des vues partielles de l'objet, potentiellement corrélées.Notion d'observable
Très curieusement, une grandeur physique, appelée une observable, n'est plus une fonction f (x,p) réelle, mais est représentée par un opérateur hermitien
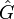 agissant sur un espace de Hilbert
agissant sur un espace de Hilbert  . La valeur de cette grandeur physique est l'une des valeurs propres réelles de cet opérateur [2] :
. La valeur de cette grandeur physique est l'une des valeurs propres réelles de cet opérateur [2] :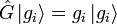
Si l'état du système à l'instant de la mesure est un vecteur
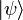 de l'espace
de l'espace  , alors ce vecteur admet la décomposition :
, alors ce vecteur admet la décomposition :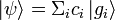
où les ci sont des nombres complexes.
Interprétation probabiliste
Le nombre complexe ci permet de calculer la probabilité pi d'obtenir la valeur gi :
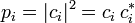 .
.La mesure de la grandeur est donc une variable aléatoire (v.a.) avec une espérance E(g) et un écart type σ(g) [3]. La mesure est donc de nature probabiliste, ce qui implique beaucoup de paradoxes apparents en logique aristotélicienne. L'un d'entre eux a été immédiatement remarqué par Heisenberg : comme l'opérateur position
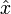 et l'opérateur quantité de mouvement
et l'opérateur quantité de mouvement 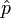 ne commutent pas :
ne commutent pas :![\left[ \hat{q} , \hat{p} \right] = i \, \hbar \,\hat{\Bbb{I}}](/pictures/frwiki/55/7a55238103043d11b06bc2325aac9c5f.png)
on ne peut pas mesurer simultanément ces deux grandeurs : la notion d'espace des phases disparaît en mécanique quantique. L'objet quantique est en fait complètement décrit par sa fonction d'onde. Les grandeurs scalaires utilisées en physique classique sont insuffisantes et inadéquates.
L'évolution déterministe de Newton est remplacée par une équation d'évolution déterministe de Schrödinger, permettant de prédire de façon certaine l'évolution temporelle des fonctions d'onde (dont le module carré est la probabilité, la phase n'étant pas connue a priori).
Inégalité de Heisenberg
Des mesures répétées de la position et de l'impulsion donneront des résultats en général différents à chaque mesure : chaque échantillon de valeurs sera caractérisé par un écart type : σx pour la position, et σp pour l'impulsion. Le théorème de Heisenberg démontre que :
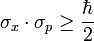 ,
,
où
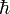 est la constante de Planck réduite. Cette notion est fréquemment vulgarisée par des phrases du type : « Il est impossible de connaître à la fois la position et la quantité de mouvement d’un objet de manière précise ». En effet, si par exemple la position d'une particule est exactement connue, la dispersion en position est identiquement nulle : σx = 0. L'inégalité de Heisenberg implique alors que
est la constante de Planck réduite. Cette notion est fréquemment vulgarisée par des phrases du type : « Il est impossible de connaître à la fois la position et la quantité de mouvement d’un objet de manière précise ». En effet, si par exemple la position d'une particule est exactement connue, la dispersion en position est identiquement nulle : σx = 0. L'inégalité de Heisenberg implique alors que 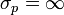 : la dispersion en impulsion doit être maximale.
: la dispersion en impulsion doit être maximale.Principe général de Heisenberg
Le théorème de Heisenberg ne s’applique pas seulement au couple de valeurs position et quantité de mouvement. Dans sa forme générale, il s’applique à chaque couple d'opérateurs
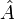 et
et 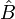 ne commutant pas :
ne commutant pas :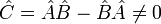
Énoncé du principe de Heisenberg
Pour un état
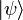 donné, on a :
donné, on a :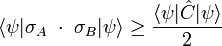
où la valeur moyenne du commutateur
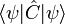 dépend bien sûr de l'état
dépend bien sûr de l'état 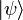 choisi.
choisi.Ce théorème général, conséquence de l’inégalité de Cauchy-Schwarz, fut mis en évidence en 1930 par Robertson et (indépendamment) par Schrödinger ; l'inégalité est donc aussi connue comme la relation de Robertson-Schrödinger.
Principe ou théorème ?
Les puristes réservent parfois le nom de principe au cas où un minorant non nul de
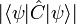 existe quel que soit l'état
existe quel que soit l'état 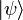 . Cela n'est possible que si l'espace de Hilbert est de dimension infinie. En effet, dans le cas d'un espace de dimension finie, on a :
. Cela n'est possible que si l'espace de Hilbert est de dimension infinie. En effet, dans le cas d'un espace de dimension finie, on a :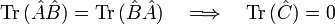
Il n'y a alors que théorème de Heisenberg, et non pas principe; c'est par exemple le cas d'un spin 1/2.
Autre formulation du principe de Heisenberg
L'inégalité de Heisenberg est souvent écrite :
![\Delta{A} \cdot \Delta{B} \ge \frac{1}{2} \left| \left\langle \left[ \hat{A}, \hat{B} \ \right] \right\rangle_\gamma \right|](/pictures/frwiki/55/7cb2703eac36a28d1371aec39fb4f194.png)
où :
- A et B sont deux observables,
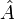 et
et 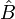 les opérateurs correspondants,
les opérateurs correspondants,
![[\hat{A},\hat{B}]](/pictures/frwiki/99/c081d8bf21108f8283f018b863a75393.png) représente le commutateur de
représente le commutateur de 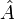 et
et 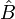 ,
,
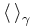 est la moyenne sur l’état notation bra-ket :
est la moyenne sur l’état notation bra-ket : 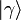 , et
, et
- Δ X est l’écart type de X :
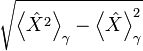 .
.
Relation temps-énergie
Il existe également une relation d'incertitude portant sur l'énergie d'une particule et la variable temps. Ainsi, la durée Δt nécessaire à la détection d'une particule d'énergie E à ΔE près[4] vérifie la relation :
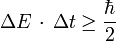
Cependant, la déduction de cette inégalité énergie-temps est assez différente de celle des inégalités position-impulsion[5]. En effet, si le Hamiltonien est bien le générateur des translations dans le temps en mécanique hamiltonienne, indiquant que temps et énergie sont conjugués[6], il n'existe pas d'opérateur temps en mécanique quantique (« théorème » de Pauli), c’est-à-dire qu'on ne peut pas construire d'opérateur
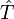 qui obéirait à une relation de commutation canonique avec l'opérateur Hamiltonien
qui obéirait à une relation de commutation canonique avec l'opérateur Hamiltonien 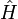 :
:![\left[ \hat{H} , \hat{T} \right] = i \hbar \hat{\Bbb{I}}](/pictures/frwiki/102/f34f47b6cc3414bcd9345b4893806846.png)
ceci pour une raison très fondamentale : la mécanique quantique a en effet été inventée pour que chaque système physique stable possède un état fondamental d'énergie mininum[7].
Perspective historique
Il est clair que l'abandon de la logique d'Aristote à cause de la nature probabiliste de la mesure a suscité un vif émoi dans la communauté scientifique : John von Neumann est un des tous premiers à écrire sur la logique quantique[8], suivi par Mackey[9].
La controverse Einstein-Bohr est par ailleurs célèbre : pour Einstein, « Dieu ne joue pas aux dés ! », ce à quoi Bohr répondra : « Einstein, cessez de dire à Dieu ce qu'Il doit faire ». Le paradoxe EPR entraînera Bell via ses inégalités à renoncer à la notion classique de localité[10]. Cette hypothèse sera confirmée par l'expérience d'Aspect en 1982; cette expérience sera encore raffinée par Anton Zeilinger en 1998[11]. Le paradoxe du chat de Schrödinger conduira à une réflexion profonde sur le rôle du couplage à l'environnement et la décohérence des intricats[12],[13],[14]. D'où la progression fulgurante de la cryptologie quantique, de la téléportation quantique, réalités techniques en 2005, et de l'informatique quantique, encore balbutiante en 2005.
Difficulté d'interprétation
Exemples
Cette corrélation d'incertitudes est parfois expliquée de manière erronée en affirmant que la mesure de la position modifie obligatoirement la quantité de mouvement d'une particule. Heisenberg lui même offrit initialement cette explication en 1927. Cette modification ne joue aucun rôle, car le théorème s'applique même si la position est mesurée dans une copie du système, et la quantité de mouvement dans une autre copie parfaitement identique.
Une meilleure analogie serait la suivante : soit un signal variable dans le temps, comme une onde sonore, et soit à connaître la fréquence exacte de ce signal à un instant t précis. Ceci est impossible en général, car pour déterminer précisément la fréquence, il faut échantillonner le signal pendant une certaine durée [15]. En traitement du signal, cet aspect est au cœur de l'approche temps-fréquence du spectrogramme où l'on utilise le principe d'incertitude sous la formulation de Gabor.
Le théorème d'Heisenberg s'applique en particulier à l'expérience cruciale des fentes d'Young avec un photon unique : toutes les ruses qu'inventent les physiciens pour tenter de voir passer la "particule" à travers un des trous, détruisent la phase et donc les interférences de l'onde : il y a complémentarité de Bohr, c’est-à-dire que si avant toute mesure , l'état quantique | ψ > décrit à la fois un aspect ondulatoire et un aspect corpusculaire, après la mesure , il subsiste un aspect ondulatoire ou un aspect corpusculaire. Selon la phrase célèbre de Dirac , la « particlonde[16] » a interféré avec elle-même.
Cette expérience est présentée au Palais de la Découverte avec une source de photon unique. Le motif produit par des millions de photons passant à travers les fentes peut être calculé à l'aide de la mécanique quantique, mais le chemin de chaque photon ne peut être prédit par aucune méthode connue. L'interprétation de Copenhague dit qu'il ne pourra être calculé par aucune méthode. En 2005, on a même réussi cette expérience avec des fullerènes, ces grosses molécules de carbone contenant 60 atomes !
La controverse Bohr-Einstein
Einstein n'aimait pas le théorème d'incertitude. Lors du 5e congrès Solvay (1927), il soumit à Bohr un fameux défi expérimental : nous remplissons une boîte avec un matériau radioactif qui émet de manière aléatoire une radiation. La boîte a une fente qui est ouverte et immédiatement fermée par une horloge de précision, permettant à quelques radiations de sortir. Donc le temps est connu avec précision. Nous voulons toujours mesurer précisément l'énergie qui est une variable conjuguée. Aucun problème, répond Einstein, il suffit de peser la boîte avant et après. Le principe d'équivalence entre la masse et l'énergie donnée par la relativité restreinte permet ainsi de déterminer précisément l'énergie qui a quitté la boîte. Bohr lui répondit ceci : si de l'énergie avait quitté le système alors la boîte plus légère serait montée sur la balance. Ce qui aurait modifié la position de l'horloge. Si l'horloge dévie de notre référentiel stationnaire, par la relativité restreinte il s'ensuit que sa mesure du temps diffère de la nôtre, ce qui conduit inévitablement à une marge d'erreur. En fait l'analyse détaillée montre que l'imprécision est donnée correctement par la relation d'Heisenberg. Voir par exemple le site de la fondation Nobel pour une figure de cette « horloge dans la boîte ».
Dans l'interprétation de Copenhague de la mécanique quantique, largement acceptée mais pas universellement, le théorème d'incertitude implique qu'à un niveau élémentaire, l'univers physique ne « vit » pas dans un espace des phases, mais plutôt comme un ensemble de réalisations potentielles, exactement déterminées en probabilité : les probabilités sont, elles, déterminées avec une précision absolue, pour autant que l'état du système soit pur (c’est-à-dire qu'il ne soit pas lui-même déterminé approximativement !)
États comprimés
Pour contourner les inégalités d'Heisenberg, les physiciens réalisent des états dits comprimés (en franglais : états « squeezés »), où il n'y a aucune incertitude sur la phase (mais alors le nombre de particules est indéterminé) ou, au contraire, un nombre bien déterminé de particules (en particulier de photons), mais on perd l'information sur la phase. Il a été montré par les travaux de Glauber que l'information quantique n'est pas entachée par le théorème d'Heisenberg. On peut donc espérer tirer le maximum d'information quantique d'une photographie numérique, tout en respectant le deuxième principe de la thermodynamique[17].
Notes
- ↑ Jean-Marc Lévy- Leblond et Françoise Balibar, When did the indeterminacy principle become the uncertainty principle ?, Physics 66, 1998, p. 278- 279, cité par Etienne Klein dans [1] page 6
- ↑ On note gi la valeur propre associée au vecteur propre
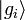 . Par souci de simplification, on néglige ici la notion de multiplicité des valeurs propres.
. Par souci de simplification, on néglige ici la notion de multiplicité des valeurs propres. - ↑ Plus généralement, tous les moments peuvent être définis.
- ↑ Ce concept est primordial en théorie quantique des champs, théorie qui fait appel à la notion de particule virtuelle.
- ↑ Pour une dérivation rigoureuse de l'inégalité énergie-temps, consulter par exemple : Albert Messiah, Mécanique quantique [détail des éditions] vol. 1 p. 114-117, p. 269-270, et enfin, pour l'oscillateur harmonique, p. 280.
- ↑ De même que la composante pi de l'impulsion est le générateur des translations d'espace dans la direction xi.
- ↑ L'argument de Pauli est le suivant : si l'opérateur temps existait, il posséderait un spectre continu. Or, l'opérateur temps, obéissant à la relation de commutation canonique, serait aussi le générateur des translations en énergie. Ceci entraîne alors que l'opérateur hamiltonien posséderait lui aussi un spectre continu et infini dans les deux sens, en contradiction avec le fait que l'énergie de tout système physique stable se doit d'être bornée inférieurement. Concernant la validité de ce « théorème », lire les travaux très récents d'Eric Galapon : quant-ph/9908033 et quant-ph/0303106.
- ↑ George Birkhoff and John von Neumann, The Logic of Quantum Mechanics, Annals of Mathematics 37 (1936), pp. 823-843.
- ↑ George Mackey, Mathematical Foundations of Quantum Mechanics, W. A. Benjamin (1963). Réédité par Dover (2004), ISBN 0-486-43517-2.
- ↑ John S. Bell ; Phys 1 (1964) 195.
- ↑ Alain Aspect ; Quelques tests expérimentaux des fondements de la mécanique quantique (en optique), Qu'est-ce que l'Univers ?, Vol. 4 de l'Université de Tous les Savoirs (sous la direction d'Yves Michaux), Odile Jacob (2001), ISBN 2-7381-0917-9, pp. 589. Dualité onde-corpuscule, intrication quantique & paradoxe E.P.R., par un professeur d'optique à l'Université de Paris-Sud (Orsay), auteur en 1982 d'une remarquable expérience testant les inégalités de Bell des corrélations E.P.R. (expérience en faveur des prédictions de la mécanique quantique. Cette expérience fût améliorée en 1998 par Anton Zeilinger et ses collaborateurs de l'Université d'Innsbrück, Autriche).
- ↑ Serge Haroche, Jean-Michel Raimond & Michel Brune ; Le chat de Schrödinger se prête à l'expérience - Voir en direct le passage du monde quantique au monde classique, La Recherche 301 (Septembre 1997) 50. Lire aussi : Serge Haroche ; Une exploration au cœur du monde quantique, dans : Qu'est-ce que l'Univers ?, Vol. 4 de l'Université de Tous les Savoirs (sous la direction d'Yves Michaux), Odile Jacob (2001), ISBN 2-7381-0917-9, pp. 571.
- ↑ Roland Omnès ; Comprendre la mécanique quantique, EDP Sciences (2000) ISBN 2-86883-470-1. Par un professeur de physique théorique émérite de l'Université de Paris-Sud (Orsay), une discussion de l' interprétation de Copenhague de la mécanique quantique, du problème de la mesure et de la théorie des histoires consistantes de Griffiths et de la décohérence, par l'un de ses pionniers.
- ↑ La décohérence, Séminaire Poincaré (19 novembre 2005).
- ↑ Techniquement, le temps et la fréquence sont ici des variables conjuguées au sens de la transformée de Fourier.
- ↑ Jean-Marc Lévy-Leblond a proposé d'utiliser plutôt le terme de quanton : Jean-Marc Lévy-Leblond & Françoise Balibar ; Quantique : rudiments, InterEditions/Editions du CNRS (1984). Réédité par Masson (1997) ISBN 2-225-85521-8, aujourd'hui racheté par Dunod : ISBN 2-225-85521-8.
- ↑ Voir par exemple les travaux de Claude Fabre (Laboratoire Kastler-Brossel, université Paris 6).
Voir aussi
- Mécanique quantique
- Dualité onde-particule
- Louis de Broglie
- Werner Heisenberg
- Saturation des inégalités d'Heisenberg
- Logique quantique
- paradoxe de la flèche
Bibliothèque virtuelle
- David C. Cassidy ; Werner Heisenberg and the uncertainty principle. Site proposé par l'auteur (Université Hofstra) et le Center for History of Physics de l' American Institute of Physics.
Bibliographie
- David C. Cassidy ; Uncertainty - The life & science of Werner Heisenberg, Freeman & Co. (1992) ISBN 0-7167-2503-7
- Werner Heisenberg ; Les principes physiques de la théorie des quanta, Gauthier-Villars (1932). Réédition par Jacques Gabay (1989) ISBN 2-87647-080-2
- John von Neumann ; Les fondements mathématiques de la mécanique quantique, Springer-Verlag (1932). Traduction française : Librairie Alcan (1946), réédité par Jacques Gabay (1988), ISBN 2-87647-047-0.
- George Birkhoff and John von Neumann, The Logic of Quantum Mechanics, Annals of Mathematics 37 (1936), pp. 823-843.
- George Mackey, Mathematical Foundations of Quantum Mechanics, W. A. Benjamin (1963). Réédité par Dover (2004), ISBN 0-486-43517-2.
- John S. Bell ; Phys 1 (1964) 195.
- Alain Aspect ; Quelques tests expérimentaux des fondements de la mécanique quantique (en optique), Qu'est-ce que l'Univers ?, Vol. 4 de l'Université de Tous les Savoirs (sous la direction d'Yves Michaux), Odile Jacob (2001), ISBN 2-7381-0917-9, pp. 589. Dualité onde-corpuscule, intrication quantique & paradoxe E.P.R., par un professeur d'optique à l'Université de Paris-Sud (Orsay), auteur en 1982 d'une remarquable expérience testant les inégalités de Bell des corrélations E.P.R. (expérience en faveur des prédictions de la mécanique quantique. Cette expérience fût améliorée en 1998 par Anton Zeilinger et ses collaborateurs de l'Université d'Innsbrück, Autriche).
- Serge Haroche, Jean-Michel Raimond & Michel Brune ; Le chat de Schrödinger se prête à l'expérience - Voir en direct le passage du monde quantique au monde classique, La Recherche 301 (Septembre 1997) 50. Lire aussi : Serge Haroche ; Une exploration au cœur du monde quantique, dans : Qu'est-ce que l'Univers ?, Vol. 4 de l'Université de Tous les Savoirs (sous la direction d'Yves Michaux), Odile Jacob (2001), ISBN 2-7381-0917-9, pp. 571.
- Roland Omnès ; Comprendre la mécanique quantique, EDP Sciences (2000) ISBN 2-86883-470-1. Par un professeur de physique théorique émérite de l'Université de Paris-Sud (Orsay), une discussion de l' interprétation de Copenhague de la mécanique quantique, du problème de la mesure et de la théorie des histoires consistantes de Griffiths et de la décohérence, par l'un de ses pionniers.
- La décohérence, Séminaire Poincaré (19 novembre 2005).
Liens externes
- (en) The certainty principle, revue
- Portail de la physique
Catégories : Physique théorique | Mécanique quantique | Principe physique
Wikimedia Foundation. 2010.