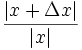Stabilite numerique

Stabilite numerique

Stabilité numérique

En analyse numérique une branche des mathématiques, la stabilité numérique est une propriété des algorithmes numériques. La définition précise de la stabilité dépend du contexte, mais elle concerne l'exactitude des résultats fournis par un algorithme. Elle décrit comment les erreurs dans les données d'entrée sont propagées à travers un algorithme.

Parfois un calcul peut être réalisé de plusieurs manières, lesquelles sont toutes algébriquement équivalentes et donnent théoriquement le même résultat, mais dans la pratique elles donnent des résultats différents car elles ont différents niveaux de stabilité numérique. Une des tâches communes de l'analyse numérique est d'essayer de trouver les algorithmes les plus robustes, c'est-à-dire ayant la meilleure stabilité numérique.

Dans une méthode stable, les erreurs restent minimes et les résultats produits sont conformes à ceux attendus. Dans une méthode instable, les erreurs de calcul sont amplifiées par le traitement et altèrent le résultat final. Des méthodes instables produisent rapidement des résultats aberrants et sont inutiles pour le traitement numérique.

Sommaire

Stabilité inverse

Considérons un problème résolu au moyen d'un algorithme numérique considéré comme une fonction f qui associe à la donnée x la solution y. Le résultat réel noté y * , s'écartera en général de la solution exacte. Les principales causes sont les erreurs d'arrondi, les erreurs de troncature et les erreurs de donnée. L'erreur aval d'un algorithme est la différence entre le résultat réel et la solution exacte. L'erreur amont ou erreur inverse est le plus petit Δx tels que 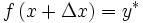f\left(x+\Delta x\right)=y^*; en d'autres termes, l'erreur amont nous indique de quelle façon le problème est réellement résolu par l'algorithme. Les erreurs amont et aval sont reliées par le nombre condition: l'erreur aval possède tout au plus le même ordre de grandeur que le nombre condition multiplié par l'ordre de grandeur de l'erreur amont.

L'algorithme est dit inversement stable ou stable en amont si l'erreur amont est assez petite pour toutes les données x. Bien sûr « petit » est un terme relatif, et sa définition dépendra du contexte. Souvent il est exigé que l'erreur soit du même ordre que..., ou seulement plus grande que ... de quelques ordres de grandeur, à une unité près.

Dans beaucoup de situations, il est plus naturel de considérer l'erreur relative

\frac{|x+\Delta x|}{|x|}

à la place de l'erreur absolue Δx.

Stabilité mixte

Stabilité des méthodes numériques de résolution des équations différentielles

Références

  • (en) Nicholas J. Higham, Accuracy and Stability of Numerical Algorithms, Society of Industrial and Applied Mathematics, Philadelphia, 1996. ISBN 0-89871-355-2.
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Stabilit%C3%A9 num%C3%A9rique ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Stabilite numerique de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Stabilité numérique — En analyse numérique, une branche des mathématiques, la stabilité numérique est une propriété globale d’un algorithmique numérique, une qualité nécessaire pour espérer obtenir des résultats ayant du sens. Une définition rigoureuse de la stabilité …   Wikipédia en Français

  • STABILITÉ — Pour un ensemble mécanique (D), dont la situation par rapport à un repère galiléen (g ) est caractérisée par la donnée de n paramètres géométriques indépendants (q 1, ..., qi , ..., qn ), la connaissance des conditions initiales et des champs de… …   Encyclopédie Universelle

  • Stabilité — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Stabilité », sur le Wiktionnaire (dictionnaire universel) Stabilité peut se référer à : Stabilité …   Wikipédia en Français

  • NUMÉRIQUE (ANALYSE) — Les problèmes et les méthodes numériques ne délimitent pas un secteur spécifique des mathématiques; ils interviennent en effet non seulement dans les domaines traditionnels (analyse classique et équations fonctionnelles), mais aussi en algèbre,… …   Encyclopédie Universelle

  • Stabilite (d'un schema numerique) — Stabilité d un schéma numérique Un schéma numérique est dit stable lorsque la différence entre la solution numérique obtenue et la solution exacte des équations discrétisées est bornée. La solution numérique doit vérifier l équation d origine… …   Wikipédia en Français

  • Stabilité (d'un schéma numérique) — Stabilité d un schéma numérique Un schéma numérique est dit stable lorsque la différence entre la solution numérique obtenue et la solution exacte des équations discrétisées est bornée. La solution numérique doit vérifier l équation d origine… …   Wikipédia en Français

  • Stabilité d'un schéma numérique — En analyse numérique, la stabilité d’un schéma numérique aux différences finies est une propriété globale de l’algorithme qui en découle. Elle concerne essentiellement le comportement numérique qui se manifeste lorsque les pas de discrétisation… …   Wikipédia en Français

  • Stabilité écologique — Dynamique écologique dynamique écologique La théorie du (Patch Dynamics Concept ou PDC pour les anglophones d après Thompson, en 1978) est de plus en plus utilisée, notamment dans le domaine de l écologie du paysage pour l étude des dynamiques… …   Wikipédia en Français

  • Analyse Numérique — Simulation numérique d un crash de véhicule L’analyse numérique est une discipline des mathématiques. Elle s’intéresse tant aux fondements théoriques qu’à la mise en pratique des méthodes permettant de résoudre, par des calculs purement… …   Wikipédia en Français

  • Analyse numerique — Analyse numérique Simulation numérique d un crash de véhicule L’analyse numérique est une discipline des mathématiques. Elle s’intéresse tant aux fondements théoriques qu’à la mise en pratique des méthodes permettant de résoudre, par des calculs… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”