- Inégalité de Cramér-Rao
-
Borne FDCR
En statistique, la borne FDCR (autrement appelée inégalité de Cramér-Rao), appelée ainsi en l'honneur de Fréchet, Darmois, Cramer et Rao, exprime une borne inférieure sur la variance d'un estimateur sans biais, basée sur l'Information de Fisher.
Elle énonce que l'inverse de l'information de Fisher,
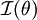, d'un paramètre θ, est une borne inférieure de la variance d'un estimateur sans biais de ce paramètre. (noté 
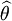).Dans certains cas, aucun estimateur non biaisé n'atteint la borne inférieure.
Exemple
Supposons que X est une variable aléatoire qui suit une loi normale d' espérance connue μ et de variance inconnue σ2. Considérons T l'estimateur de σ2:
Alors T est non biaisé pour σ2, car E(T) = σ2. Quelle est la variance de T?
Le premier terme est le quatrième moment central et vaut 3(σ2)2; le second est le carré de la variance, soit (σ2)2. Donc
Quelle est l'information de Fisher de cet exemple ? Le score V est défini par
avec L étant la Fonction de vraisemblance. Donc, dans ce cas,
L'information de nn évènement indépendant étant seulement n fois l'information d'un seul évènement, soit
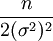.L'Inégalité de Cramér-Rao donne :
Dans ce cas, on a donc égalité, ce qui montre que l'estimateur est efficace.
Conditions de régularité
Cette inégalité repose sur 2 conditions faibles de régularité des densité de probabilité, f(x;θ), et l'estimateur T(X):
- L'information de Fisher est toujours définie; de manière équivalente, pour tout x tel que f(x;θ) > 0,
- soit fini.
- L'intégration par rapport à x et la différentiation par rapport à θ peuvent être échangé dans le calcul de T; soit encore,
- si le second membre est fini.
Dans certains cas, un estimateur biaisé peut avoir une variance et une erreur quadratique moyenne en dessous de la borne de Cramér-Rao (cette borne ne s'appliquant que pour les estimateurs non biaisés).
Si la régularité permet d'atteindre la dérivée seconde, alors l'information de Fisher peut se mettre sous une autre forme, et l'inégalité de Cramér-Rao donne:
Portail des probabilités et des statistiques
Catégorie : Estimation (statistique)
![\mathrm{var} \left(\widehat{\theta}\right)
\geq
\frac{1}{\mathcal{I}(\theta)}
=
\frac{1}
{
\mathrm{E}
\left[
\left[
\frac{\partial}{\partial \theta} \log f(X;\theta)
\right]^2
\right]
}](/pictures/frwiki/100/d67d8ff413670eb911477fab82d7b848.png)
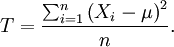
![\mathrm{Var}(T) = \frac{\mathrm{var}(X-\mu)^2}{n}=\frac{1}{n}
\left[
E\left\{(X-\mu)^4\right\}-\left(E\left\{(X-\mu)^2\right\}\right)^2
\right]](/pictures/frwiki/54/6458c15421b39b317cff6436d876cee9.png)
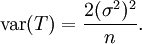
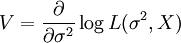
![V=\frac{\partial}{\partial\sigma^2}\log\left[\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(X-\mu)^2/{2\sigma^2}}\right]
=\frac{(X-\mu)^2}{2(\sigma^2)^2}-\frac{1}{2\sigma^2}](/pictures/frwiki/50/27dd82a154b9065c0fa7dae49cdff274.png)
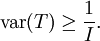
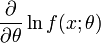
![\frac{\partial}{\partial\theta}
\left[
\int T(x) f(x;\theta) \,dx
\right]
=
\int T(x)
\left[
\frac{\partial}{\partial\theta} f(x;\theta)
\right]
\,dx](/pictures/frwiki/53/5cb7f5b7531809bf154687fe9a8d4d7b.png)
![\mathrm{var} \left(\widehat{\theta}\right)
\geq
\frac{1}{\mathcal{I}(\theta)}
=
\frac{1}
{
-\mathrm{E}
\left[
\frac{d^2}{d\theta^2} \log f(X;\theta)
\right]
}](/pictures/frwiki/52/498f244f1681ef9e7bd749a0c53bbf0f.png)
Wikimedia Foundation. 2010.
