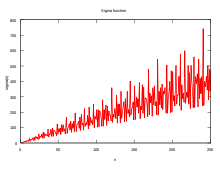
- Somme des diviseurs
-
En arithmétique, la somme des diviseurs d'un nombre entier strictement positif est l'entier obtenu en effectuant la somme de tous les diviseurs positifs de cet entier.
La fonction qui, à l'entier n, associe la somme de ses diviseurs est souvent notée σ.
Ainsi σ(6) = 1 + 2 + 3 + 6 = 12 , σ(p) = p + 1 pour tout nombre premier p et σ(1) = 1.
Cette fonction intervient dans l'étude des nombres parfaits, amiables, déficients ou abondants, des nombres intouchables ou sublimes ou dans les suites aliquotes. Elle est aussi étudiée dans le cadre de l'hypothèse de Riemann.
C'est un exemple de fonction multiplicative.
On étudie aussi parfois la somme des diviseurs propres de n. C'est l'entier obtenu en effectuant la somme de tous les diviseurs positifs de n strictement inférieurs à n. Si on appelle s(n) ce nombre, on a la relation suivante :
- s(n) = σ(n) − n
Sommaire
Propriétés
La fonction σ est une fonction multiplicative, c'est-à-dire que, pour tout entier a et b premiers entre eux,

En effet, si a et b sont premiers entre eux, d est un diviseur de ab si et seulement si d peut s'écrire dadb où da est un diviseur de a et db un diviseur de b, cette décomposition est unique. Un regroupement judicieux des diviseurs dans le calcul de σ(ab) permet alors de conclure :
La somme des termes d'une suite géométrique permet de calculer la somme des diviseurs d'une puissance d'un nombre premier :
L'utilisation des deux propriétés précédentes permet de déterminer la somme des diviseurs de n connaissant sa décomposition en facteurs premiers. Si
alors
Loi d'Euler
Léonard Euler énonce en 1752[1] un résultat qu'il appelle Loi tout extraordinaire des nombres par rapport à la somme de leurs diviseurs permettant de déterminer la somme des diviseurs de n à l'aide d'une formule de récurrence:
où 1, 2, 5, 7, 12, est la suite des nombres pentagonaux généralisés
 avec
avec
avec
- fn(k) = σ(k) si k > 0
- fn(0) = n
- fn(k) = 0 si k <0
Loi qu'il démontre en 1754[2] à l'aide de l'écriture en série d'un produit infini :
Somme des diviseurs et hypothèse de Riemann
La fonction somme des diviseurs a été étudiée dans le cadre de la démonstration de l'hypothèse de Riemann.
J. Lagarias lie la somme des diviseurs à la série harmonique (Hn) et prouve[3] que l'hypothèse de Riemann est vraie si et seulement si :
- pour tout entier n,

Il a aussi été prouvé (théorème de Grönwall[4] - 1913) que
où eγ est la constante d'Euler-Mascheroni
Le critère de Robin[5] (1984) stipule que l'hypothèse de Riemann est vraie si et seulement si
pour tout
 .
.Cette inégalité a déjà été établie pour 70% des entiers naturels[6]
Notes et références
- Léonheard Euler, Commentationes arithmeticae collectae, volume I , Observatio de summis divisorum p 148
- Léonheard Euler, Commentationes arithmeticae collectae, volume I , Demonstration theorematis circa ordinem in summis divisorum observatum p 234
- Jeffrey C. Lagarias, 'An Elementary Problem equivalent to the Riemann Hypothesis, mai 2001
- Weisstein, Eric W. "Gronwall's Theorem." From MathWorld--A Wolfram Web Resource.
- Weisstein, Eric W. "Robin's Theorem." From MathWorld--A Wolfram Web Resource.
- Patrick Solé, Somme de diviseurs et hypothèse de Riemann
Bibliographie
- G Halphéen, Sur diverses formules récurrentes concernant les diviseurs des nombres entiers, Bulletin de la S.M.F., tome 6 (1878), pp 173 - 188
- Léonheard Euler, Commentationes arithmeticae collectae, volume I
Voir aussi
Catégories :- Divisibilité et factorisation
- Fonction arithmétique
Wikimedia Foundation. 2010.