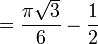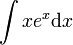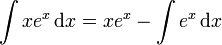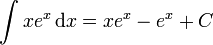- Intégration par partie
-
Intégration par parties
En mathématiques, l'intégration par parties est une méthode qui permet de transformer l'intégrale d'un produit de fonctions en d'autres intégrales, dans un but de simplification du calcul.
La formule-type est la suivante, où u et v sont deux fonctions dérivables, de dérivées continues et a et b deux réels de leur intervalle de définition :
ou encore, en remarquant que u'(x)dx et v'(x)dx sont respectivement les différentielles de u et de v :
On peut étendre ce théorème aux fonctions continues et de classe C1 par morceaux sur le segment d'intégration
Démonstration
La démonstration de cette formule est très simple : en effet, elle découle directement de la règle du produit, soit u et v : (uv)' = u'v + uv'.
On a donc uv' = (uv)' − u'v puis :
Ce qui donne bien la propriété énoncée ci-dessus.
Cette démonstration peut également être faite à l'aide de la notation de Leibniz. Soit deux fonctions dérivables u et v. La règle de la dérivation d'un produit nous donne :
En multipliant par dx on obtient :
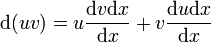
- d(uv) = udv + vdu
On réarrange ensuite l'expression de la façon suivante :
- udv = d(uv) − vdu
Il suffit maintenant d'intégrer l'équation :
On obtient alors :
Grâce à la formule de Leibniz, on peut généraliser cette méthode aux fonctions de classe Ck + 1 :
La règle employée pour dériver est l'ordre LPET. L'on commence par les fonctions logarithmiques puis polynomiales, exponentielles et enfin trigonométriques.
Choix des variables
Le choix des fonctions u et v' est arbitraire, il requiert de la pratique et de l'intuition. Cependant, après l'exemple ci dessous, quelques règles peuvent être posées pour gagner du temps.
si on choisit u = ln(x), on a u' = 1 / x et v' = x donc v = x2 / 2, d'où :
En revanche si on choisit u = x on a u' = 1 et v' = ln(x) donc v = xln(x) − x, d'où :
On constate immédiatement que cette intégrale est plus compliquée que l'intégrale initiale.
Exemples
Effectuons le calcul de :
grâce à une intégration par parties. Pour cela, nous posons :
- f(x) = x, de telle sorte que f'(x) = 1,
- g'(x) = cos(x), de telle sorte que g(x) = sin(x), par exemple.
Il vient :
Effectuons le calcul de l'intégrale indéfinie suivante :
Pour l'intégration par parties posons :
- u = x et dv = exdx
Nous avons donc :
- du = dx et v = ex
Utilisons la formule de l'intégration par parties :
L'intégrale est maintenant beaucoup plus simple à calculer. On trouve :
- Portail des mathématiques
Catégorie : Méthode d'intégration
Wikimedia Foundation. 2010.

![\int_a^b u(x) v'(x)\,\mathrm dx = \Bigl[u(x) v(x)\Bigr]_a^b - \int_a^b u'(x) v(x) \,\mathrm dx](/pictures/frwiki/49/13532db9a62757abdf2c5d9f59f23fe1.png)
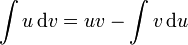
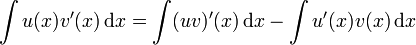
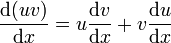
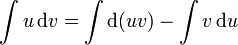
![\int_{a}^{b} f(x) g^{(k+1)}(x)\,\mathrm dx = \left[ \sum_{n=0}^{k}(-1)^{n} f^{(n)}(x) g^{(k-n)}(x) \right]_{a}^{b} + (-1)^{k+1} \int_{a}^{b} f^{(k+1)}(x) g(x) \,\mathrm dx](/pictures/frwiki/51/344657b62ad08d4988223d238fd02ca4.png)
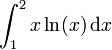
![\int_{1}^{2}x\ln(x) \,\mathrm dx = \left[\frac{x^2}{2}\ln(x)\right]_{1}^{2} - \frac{1}{2} \int_{1}^{2}x\,\mathrm dx](/pictures/frwiki/57/9c17ebf2fb960a6ba681be13b80651f2.png)
![\int_{1}^{2}x\ln(x) \,\mathrm dx = \left[x(x\ln(x) - x)\right]_{1}^{2} - \int_{1}^{2}(x\ln(x) - x)\,\mathrm dx](/pictures/frwiki/52/4a136cb1b260ea3f097bcfaeda440f93.png)
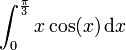
![\int_{0}^{\frac{\pi}{3}} x\cos (x) \,\mathrm dx = \left[ f(x) g(x) \right]_{0}^{\frac{\pi}{3}} - \int_{0}^{\frac{\pi}{3}} f'(x) g(x) \,\mathrm dx](/pictures/frwiki/52/410e8852636233386c61e3ce5be9eed8.png)
![= \left[x\sin (x)\right]_{0}^{\frac{\pi}{3}} - \int_{0}^{\frac{\pi}{3}} \sin (x) \,\mathrm dx](/pictures/frwiki/101/ef319de03c304689657b52e5e916895c.png)
![= \frac{\pi \sqrt{3}}{6} + \left[\cos (x)\right]_{0}^{\frac{\pi}{3}}](/pictures/frwiki/49/147270d48db8eeba77470da87ed19eda.png)