Theoreme de derivation des fonctions composees

Theoreme de derivation des fonctions composees

Théorème de dérivation des fonctions composées

En mathématiques, dans le domaine de l'analyse, le théorème de dérivation des fonctions composées (parfois appelé règle de dérivation en chaîne, selon l'appellation anglaise) est une formule explicitant la dérivée d'une fonction composée.

Sommaire

Cas réel

Énoncé et démonstration

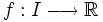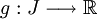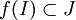Soient I et J deux intervalles de \mathbb{R}. Et soient f:I \longrightarrow \mathbb{R} et g:J \longrightarrow \mathbb{R} des fonctions telles que f(I) \subset J.

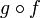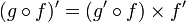Si f est dérivable sur I et g est dérivable sur f(I) alors la composée g \circ f est dérivable sur I et : (g \circ f)'=(g' \circ f)\times f'.

Il est aussi possible de l'écrire avec la notation de Leibniz sous la forme:

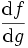\frac {\text{d}f}{\text{d}x} = \frac {\text{d}f} {\text{d}g} \frac {\text{d}g}{\text{d}x}

où \frac {\text{d}f} {\text{d}g} indique que f dépend de g comme si g était une variable.

Pour une meilleure lecture on pose souvent 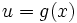u = g(x)\, et on obtient :

\frac {\text{d}}{\text{d}x} f \circ g(x) = \frac{\text{d}f(u)}{\text{d}u} \cdot \frac {\text{d}u}{\text{d}x}
Démonstration

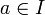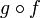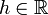Soit a \in I. D'après nos hypothèses f est dérivable en a et g en f(a). Formons la limite du taux d'accroissement de la fonction g \circ f en prenant un h \in \mathbb{R} :

\lim_{h \to 0} \frac{(g \circ f)(a+h)-(g \circ f)(a)}{h} =\lim_{h \to 0} \frac{g(f(a+h))-g(f(a))}{h}

On pose k = f(a + h) − f(a). Clairement

\lim_{h \to 0} k=0

Il vient donc

\begin{align} \lim_{h \to 0} \frac{g(f(a+h))-g(f(a))}{h}&=\displaystyle \lim_{h \to 0} \frac{g(f(a)+k)-g(f(a))}{h}\\ &=\lim_{h \to 0} \frac{g(f(a)+k)-g(f(a))}{k}\frac{k}{h}\\ &=\lim_{k \to 0} \frac{g(f(a)+k)-g(f(a))}{k} \lim_{h \to 0}\frac{k}{h}\\ &= \lim_{k \to 0} \frac{g(f(a)+k)-g(f(a))}{k} \lim_{h \to 0}\frac{f(a+h)-f(a)}{h}\\ &=g'(f(a))f'(a) \end{align}

Ce qui prouve que notre théorème est vrai au point a. On le généralise facilement à tout l'intervalle I.

Exemple

Formons la dérivée sur \mathbb{R} de ecos(x). Notre théorème indique qu'il faut d'abord dériver la fonction "la plus à l'extérieur". La dérivée de eX est eX. Maintenant on dérive "l'intérieur" : cos(x) ce qui donne − sin(x). Notre dérivée est donc : − sin(x)ecos(x).

Applications

C'est de cette règle que découle la règle du changement de variable pour le calcul d'intégrales.

Cas général

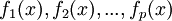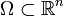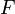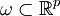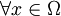On se place dans l'espace \mathbb{R}^n. Si les fonctions réelles \,f_1(x),f_2(x),... ,f_p(x) sont dérivables sur \Omega\subset\R^n et si la fonction \,F est continuement dérivable sur \omega\subset\R^p tel que [\,f_1(x),f_2(x),... ,f_p(x)]\subset\omega , \forall x\in\Omega,

alors la fonction g(x)= F[\,f_1(x),f_2(x),... ,f_p(x)] est dérivable et on a :

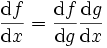
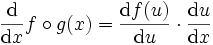
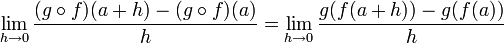
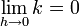
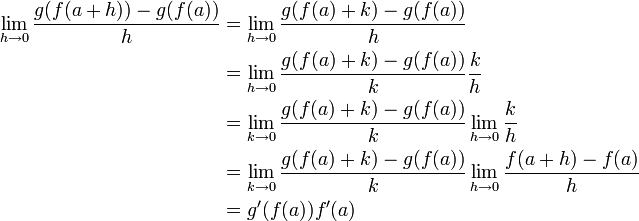
\frac{\partial g}{\partial x_k}(x)=\sum_{i=1}^{p}\frac{\partial F}{\partial f_i}[f_1 (x), f_2 (x), ... , f_p (x)]\frac{\partial f_i}{\partial x_k}(x)
  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de d%C3%A9rivation des fonctions compos%C3%A9es ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de derivation des fonctions composees de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Théorème de dérivation des fonctions composées — En mathématiques, dans le domaine de l analyse, le théorème de dérivation des fonctions composées (parfois appelé règle de dérivation en chaîne ou règle de la chaîne, selon l appellation anglaise) est une formule explicitant la dérivée d une… …   Wikipédia en Français

  • Derivation — Dérivation Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom …   Wikipédia en Français

  • Derivation sous integrale — Intégrale paramétrique En mathématiques, une intégrale paramétrique (également appelée intégrale à paramètre) est une fonction définie à partir de l intégration d une fonction de plusieurs variables sur un ensemble fixe par rapport à une partie… …   Wikipédia en Français

  • Dérivation Sous Intégrale — Intégrale paramétrique En mathématiques, une intégrale paramétrique (également appelée intégrale à paramètre) est une fonction définie à partir de l intégration d une fonction de plusieurs variables sur un ensemble fixe par rapport à une partie… …   Wikipédia en Français

  • Dérivation sous intégrale — Intégrale paramétrique En mathématiques, une intégrale paramétrique (également appelée intégrale à paramètre) est une fonction définie à partir de l intégration d une fonction de plusieurs variables sur un ensemble fixe par rapport à une partie… …   Wikipédia en Français

  • Dérivation — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Dérivation », sur le Wiktionnaire (dictionnaire universel) En mathématiques : en analyse la… …   Wikipédia en Français

  • Règle de dérivation en chaîne — Théorème de dérivation des fonctions composées En mathématiques, dans le domaine de l analyse, le théorème de dérivation des fonctions composées (parfois appelé règle de dérivation en chaîne, selon l appellation anglaise) est une formule… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Composition De Fonctions — En mathématiques, la composition de fonctions (ou composition d applications) est un procédé qui consiste, à partir de deux fonctions, d en construire une nouvelle. Pour cela on utilise les images de la première fonction comme arguments pour la… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”