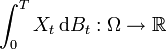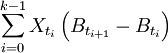Intégrale d'Itô

Intégrale d'Itô

Intégrale d'Itō

L'intégrale d'Itō, appelée ainsi en l'honneur du mathématicien Kiyoshi Itō est un des outils fondamentaux du calcul stochastique.

Il s'agit d'une intégrale définie de façon similaire à l'intégrale de Riemann comme limite d'une somme de Riemann. Si on se donne un processus de Wiener (ou mouvement brownien) B : [0, T] \times \Omega \to \mathbb{R}\, ainsi que X : [0, T] \times \Omega \to \mathbb{R} un processus stochastique adapté à la filtration naturelle associée à Bt, alors l'intégrale d'Itô

\int_{0}^{T} X_{t} \, \mathrm{d} B_{t} : \Omega \to \mathbb{R}

est définie par la limite en moyenne quadratique de

\sum_{i = 0}^{k - 1} X_{t_{i}} \left( B_{t_{i+1}} - B_{t_{i}} \right)

lorsque le pas de la partition 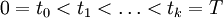0 = t_{0} < t_{1} < \dots < t_{k} = T de [0,T] tend vers 0.

Ces sommes, considérées comme des sommes de Riemann-Stieltjes pour chaque chemin du mouvement brownien donné, ne convergent pas en général; la raison en est que le mouvement brownien n'est pas à variations bornées. L'usage de la convergence quadratique est le point essentiel de cette définition.

Propriétés

Avec les notations précédentes, le processus stochastique Y défini, pour t réel positif, par 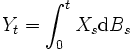Y_{t}=\int_{0}^{t}{X_{s} \mathrm{d}B_{s}}, est une martingale. En particulier, son espérance est constante.

D'autre part, on a la propriété dite d'isométrie: 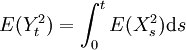E(Y_{t}^{2})=\int_{0}^{t}{E(X_{s}^{2}) \mathrm{d}s}. Noter que cette dernière intégrale est "classique", i.e. est une intégrale au sens de Riemann par rapport à la variable s.

Voir aussi

  • Portail des mathématiques Portail des mathématiques

demande de confirmation: serait aussi appelée intégrale stochastique? oui !

Ce document provient de « Int%C3%A9grale d%27It%C5%8D ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Intégrale d'Itô de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Integrale d'Ito — Intégrale d Itō L intégrale d Itō, appelée ainsi en l honneur du mathématicien Kiyoshi Itō est un des outils fondamentaux du calcul stochastique. Il s agit d une intégrale définie de façon similaire à l intégrale de Riemann comme limite d une… …   Wikipédia en Français

  • Intégrale d'Itō — L intégrale d Itō, appelée ainsi en l honneur du mathématicien Kiyoshi Itō est un des outils fondamentaux du calcul stochastique. Il s agit d une intégrale définie de façon similaire à l intégrale de Riemann comme limite d une somme de Riemann.… …   Wikipédia en Français

  • Itō (homonymie) — Ito Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Ito peut faire référence à : un des quartiers de la commune de Mayoyo dans la ville de Bandundu en République démocratique du Congo, Ito (糸), un… …   Wikipédia en Français

  • Integrale de Stieltjes — Intégrale de Stieltjes Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f …   Wikipédia en Français

  • Intégrale De Stieltjes — Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f …   Wikipédia en Français

  • Intégrale de Riemann-Stieltjes — Intégrale de Stieltjes Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f …   Wikipédia en Français

  • Intégrale de stieltjes — Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f …   Wikipédia en Français

  • Intégrale de Riemann — Interprétation géométrique de l intégrale de la fonction f. En analyse réelle, l intégrale de Riemann[1] est une façon simple de définir l intégrale d une fonction sur un …   Wikipédia en Français

  • Intégrale de Lebesgue — En mathématiques, l’intégrale de Lebesgue désigne à la fois une théorie relative à l intégration et à la mesure, puis le résultat de l intégration d une fonction à valeurs réelles définie sur (ou sur ), munis de la mesure de Lebesgue.… …   Wikipédia en Français

  • Ito — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Ito peut faire référence à : un des quartiers de la commune de Mayoyo dans la ville de Bandundu en République démocratique du Congo, Ito (糸), un nom… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”