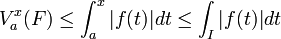Variations bornées
- Variations bornées
-
Fonction à variation bornée
En analyse, une fonction est dite à variation bornée quand elle vérifie une certaine condition de régularité. Cette condition a été introduite en 1881 par le mathématicien Camille Jordan pour étendre le Théorème de Dirichlet sur la convergence des séries de Fourier.
Définition
Soit f une fonction définie sur le compact [a,b] à valeur dans  .
.
Pour chaque subdivision ![\sigma =(a=x_0 ,x_1 ,\ldots ,x_n =b) \in \mathcal S ([a,b])](/pictures/frwiki/49/1eb41fc962e7768a965a97a5c9865013.png) , on définit V(f,σ) par :
, on définit V(f,σ) par :
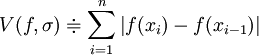 .
.
On appelle variation totale de f la valeur 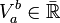 définie par :
définie par :
![V^{b}_{a}(f) \doteqdot \sup_{\sigma \in \mathcal S ([a,b])} V(f,\sigma )](/pictures/frwiki/57/9030b5fc7c1818b6bde05f4ebbc1e7da.png)
On dit que f est à variation bornée si 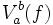 est fini.
est fini.
Plus généralement, une fonction définie sur un intervalle quelconque est à variation bornée si 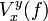 est fini quels que soient x et y dans l'intervalle.
est fini quels que soient x et y dans l'intervalle.
Propriétés
- Les fonctions à variation bornée forment un sous-espace vectoriel de l'espace des fonctions de [a,b] dans
 .
.
- Toute fonction de classe
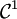 est à variation bornée, toute fonction monotone également.
est à variation bornée, toute fonction monotone également.
- Toute fonction à variation bornée est limite uniforme d'une suite de fonctions en escalier.
- Toute fonction à variation bornée est différence de deux fonctions croissantes. A fortiori, l'espace vectoriel des fonctions à variation bornée est engendré par l'ensemble des fonctions croissantes ; on en déduit également que les fonctions à variation bornée ont au plus une infinité dénombrable de points de discontinuité et sont dérivables presque partout (au sens de la mesure de Lebesgue).
- Si f est intégrable au sens de Lebesgue sur un intervalle I, alors, pour a fixé dans I la fonction
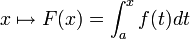 est à variation bornée. En effet,
est à variation bornée. En effet, 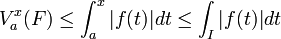
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégorie : Analyse réelle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Variations bornées de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Integrale de Stieltjes — Intégrale de Stieltjes Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f … Wikipédia en Français
Intégrale De Stieltjes — Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f … Wikipédia en Français
Intégrale de Riemann-Stieltjes — Intégrale de Stieltjes Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f … Wikipédia en Français
Intégrale de Stieltjes — Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f et … Wikipédia en Français
Intégrale de stieltjes — Thomas Stieltjes (1856–1894) L intégrale de Stieltjes constitue une généralisation de l intégrale ordinaire, ou intégrale de Riemann. En effet, considérons deux fonctions réelles bornées f … Wikipédia en Français
Conditions De Dirichlet — Théorème de Dirichlet (Séries de Fourier) En analyse, le théorème de Dirichlet (ou de Jordan Dirichlet) est un résultat de convergence ponctuelle pour les séries de Fourier. Une première version du théorème a été prouvée par Dirichlet en 1829[1] … Wikipédia en Français
Conditions de Dirichlet — Théorème de Dirichlet (Séries de Fourier) En analyse, le théorème de Dirichlet (ou de Jordan Dirichlet) est un résultat de convergence ponctuelle pour les séries de Fourier. Une première version du théorème a été prouvée par Dirichlet en 1829[1] … Wikipédia en Français
Conditions de dirichlet — Théorème de Dirichlet (Séries de Fourier) En analyse, le théorème de Dirichlet (ou de Jordan Dirichlet) est un résultat de convergence ponctuelle pour les séries de Fourier. Une première version du théorème a été prouvée par Dirichlet en 1829[1] … Wikipédia en Français
Integrale d'Ito — Intégrale d Itō L intégrale d Itō, appelée ainsi en l honneur du mathématicien Kiyoshi Itō est un des outils fondamentaux du calcul stochastique. Il s agit d une intégrale définie de façon similaire à l intégrale de Riemann comme limite d une… … Wikipédia en Français
Intégrale d'Itô — Intégrale d Itō L intégrale d Itō, appelée ainsi en l honneur du mathématicien Kiyoshi Itō est un des outils fondamentaux du calcul stochastique. Il s agit d une intégrale définie de façon similaire à l intégrale de Riemann comme limite d une… … Wikipédia en Français
 .
.![\sigma =(a=x_0 ,x_1 ,\ldots ,x_n =b) \in \mathcal S ([a,b])](/pictures/frwiki/49/1eb41fc962e7768a965a97a5c9865013.png) , on définit V(f,σ) par :
, on définit V(f,σ) par :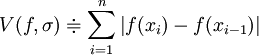 .
.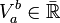 définie par :
définie par :![V^{b}_{a}(f) \doteqdot \sup_{\sigma \in \mathcal S ([a,b])} V(f,\sigma )](/pictures/frwiki/57/9030b5fc7c1818b6bde05f4ebbc1e7da.png)
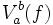 est fini.
est fini.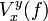 est fini quels que soient x et y dans l'intervalle.
est fini quels que soient x et y dans l'intervalle. .
.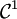 est à variation bornée, toute fonction monotone également.
est à variation bornée, toute fonction monotone également.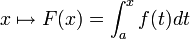 est à variation bornée. En effet,
est à variation bornée. En effet,