Algèbre Associative

Algèbre Associative

Algèbre associative

En mathématiques, une algèbre associative est un espace vectoriel dans lequel est aussi définie une multiplication des vecteurs, qui possède les propriétés de distributivité et d'associativité.

Définition

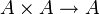Une algèbre associative A sur un corps \mathbb{K} est un espace vectoriel sur \mathbb{K} muni d'une multiplication bilinéaire A\times A \to A telle que

  • (x y) z = x (y z) pour tous x, y et z dans A,

où l'image de (x,y) est notée xy.

Si A contient une unité, i.e. un élément 1 tel que 1x=x=x1 pour tout x dans A, alors A est appelée algèbre associative unitaire. Une telle algèbre est un anneau et contient le corps de base \mathbb{K} par identification de c dans \mathbb{K} avec c1 dans A.

La dimension d'une algèbre associative A sur un corps \mathbb{K} est sa dimension comme espace vectoriel sur \mathbb{K}.

Exemples

  • Les matrices carrées de taille n par n à coefficients dans \mathbb{K} forment une algèbre associative unitaire sur \mathbb{K}.
  • Les nombres complexes \mathbb{C} forment une algèbre associative unitaire de dimension 2 sur le corps \mathbb{R} des nombres réels.
  • Les quaternions forment une algèbre associative unitaire de dimension 4 sur le corps des nombres réels.
  • Les polynômes à coefficients dans \mathbb{K} forment une algèbre associative unitaire de dimension infinie sur \mathbb{K}.
  • Pour tout espace vectoriel V, les endomorphismes de V forment une algèbre associative unitaire.
  • Les algèbres enveloppantes des algèbres de Lie sont des algèbres associatives.
  • Les algèbres d'incidence des ordres partiels localement finis sont des algèbres associatives utilisées en combinatoire.
Ce document provient de « Alg%C3%A8bre associative ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Algèbre Associative de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Algebre associative — Algèbre associative En mathématiques, une algèbre associative est un espace vectoriel dans lequel est aussi définie une multiplication des vecteurs, qui possède les propriétés de distributivité et d associativité. Définition Une algèbre… …   Wikipédia en Français

  • Algèbre associative — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, une algèbre associative (sur un anneau commutatif A) est un anneau (ou simplement un pseudo anneau) B, muni d une structure supplémentaire de module sur A et tel que la loi… …   Wikipédia en Français

  • Algèbre associative sur un anneau — En mathématiques, une algèbre associative sur un anneau est une structure algébrique sur un anneau commutatif unitaire A telle que B soit muni d une structure de A module et d une structure d anneau telle que la loi de multiplication de l anneau… …   Wikipédia en Français

  • Algèbre associative sur un corps — En mathématiques, une algèbre associative sur un corps (commutatif) est un espace vectoriel dans lequel est aussi définie une multiplication des vecteurs, qui possède les propriétés de distributivité, de bilinéarité et d associativité. Autrement… …   Wikipédia en Français

  • Algebre sur un anneau — Algèbre sur un corps En mathématiques, une algèbre est une structure algébrique qui se définit comme suit: est une algèbre sur un corps , ou autrement dit une algèbre si : (E, +, ·) est un espace vectoriel sur la loi × est définie …   Wikipédia en Français

  • Algebre sur un corps — Algèbre sur un corps En mathématiques, une algèbre est une structure algébrique qui se définit comme suit: est une algèbre sur un corps , ou autrement dit une algèbre si : (E, +, ·) est un espace vectoriel sur la loi × est définie …   Wikipédia en Français

  • Algèbre (structure) — Algèbre sur un corps En mathématiques, une algèbre est une structure algébrique qui se définit comme suit: est une algèbre sur un corps , ou autrement dit une algèbre si : (E, +, ·) est un espace vectoriel sur la loi × est définie …   Wikipédia en Français

  • Algèbre Sur Un Anneau — Algèbre sur un corps En mathématiques, une algèbre est une structure algébrique qui se définit comme suit: est une algèbre sur un corps , ou autrement dit une algèbre si : (E, +, ·) est un espace vectoriel sur la loi × est définie …   Wikipédia en Français

  • Algèbre Sur Un Corps — En mathématiques, une algèbre est une structure algébrique qui se définit comme suit: est une algèbre sur un corps , ou autrement dit une algèbre si : (E, +, ·) est un espace vectoriel sur la loi × est définie …   Wikipédia en Français

  • Algèbre sur un anneau commutatif — Algèbre sur un corps En mathématiques, une algèbre est une structure algébrique qui se définit comme suit: est une algèbre sur un corps , ou autrement dit une algèbre si : (E, +, ·) est un espace vectoriel sur la loi × est définie …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”