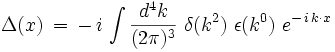Histoire de la Théorie Quantique des Champs

Cet article résume l'histoire de la théorie quantique des champs.

La théorie quantique des champs est l'application des concepts de la physique quantique aux champs. Issue de la mécanique quantique relativiste, dont l'interprétation comme théorie décrivant une seule particule s'était avérée incohérente, la théorie quantique des champs fournit un cadre conceptuel largement utilisé en physique des particules, en physique de la matière condensée, et en physique statistique.

Sommaire 1 Historique 1.1 Les premiers pas 1.2 Électrodynamique quantique 1.3 Théories de jauge 1.4 Physique statistique 2 Annexes 2.1 Article connexe 3 Bibliographie 3.1 Études d'ensemble 3.2 Références historiques 3.3 Références

Historique

Les premiers pas

En 1925 à Göttingen, peu de temps après la naissance de la mécanique des matrices, Jordan essaie de quantifier le champ électromagnétique créé par une particule chargée en suivant les nouvelles règles introduites par Heisenberg pour les particules. Cette première tentative échoue, mais Jordan persévère et, un an plus tard, essaie cette fois de quantifier le champ électromagnétique libre (i.e. en l'absence de charges). La réception de ce travail par ses pairs est plutôt hostile, et on considère usuellement que la théorie quantique des champs naît véritablement en 1927 lorsque paraît l'article princeps du britannique Dirac intitulé : « La théorie quantique de l'émission et de l'absorption du rayonnement »^[1]. Dans ce papier, Dirac quantifie complètement le système {charges + champs} en utilisant le formalisme Hamiltonien. La méthode utilisée par Dirac sera baptisée seconde quantification^[2] par Fock et Jordan en 1932.

La théorie de Dirac fut reçue et discutée élogieusement, notamment par Bohr, au cours du célèbre congrès Solvay du mois d'Octobre 1927. Cependant, elle présentait manifestement un défaut majeur : son formalisme, basé sur le Hamiltonien, faisait jouer au temps un rôle particulier, ce qui n'était pas compatible avec l'invariance de Lorentz réclamée par la théorie de la relativité restreinte d'Einstein. Heisenberg, Jordan, Pauli et Klein décidèrent alors de créer leur propre version de l'électrodynamique quantique relativiste. Dès 1927, Pauli et Jordan réussirent à formuler les relations de commutations covariantes des composantes du tenseur de Maxwell décrivant un champ électromagnétique libre quantifié (en représentation de Heisenberg) :

où η_μν est la métrique de Minkowski, et où la fonction de Pauli-Jordan Δ(x) est la généralisation relativiste de la distribution de Dirac δ(x) :

Dans cette formule, la fonction : ε(k⁰) = signe (k⁰) vaut 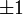selon le signe de la composante temporelle k⁰ de la quadri-implusion.

En 1933, Bohr et son collaborateur Rosenfeld analysèrent la mesurabilité du champ électromagnétique quantifié à partir des relations de commutations des composantes de celui-ci. Ils montrèrent qu'un champ quantique local en un point est un être mathématique singulier, et que seule une moyenne spatiale du champ sur une petite région de l'espace est susceptible d'être accessible à la mesure^[3]. Ils établirent des inégalités, analogues au principe d'incertitude pour une particule, qui expriment les limitations fondamentales sur la possibilité de mesurer des champs en des point d'espace-temps séparés par un intervalle du genre temps. Ce travail important fut publié dans une revue danoise sous la forme d'un article quelque peu hermétique^[4].

En plus des auteurs déjà mentionnés ci-dessus, Wigner, Weisskopf, Landau, Peierls, Oppenheimer, Podolsky, et surtout Fermi ont chacun apporté des contributions^[5] importantes au formalisme. La méthode de Fermi fut en particulier mise à profit dès 1932 par Dirac, Fock et Podolsky pour établir une formulation entièrement covariante de l'électrodynamique quantique, aussitôt incorporée par Dirac dans son célèbre ouvrage : Principes de la mécanique quantique. Cette forme finale sera reprise et synthétisée en 1943 par Wentzel dans un livre qui servira longtemps de référence^[6].

Tous les auteurs cités précédemment ont buté à un moment ou à un autre sur un obstacle récurrent : l'apparition systématique d'infinis lors des calculs de grandeurs physiques censées être mesurables, rendant la théorie inutilisable.

Électrodynamique quantique

La première véritable avancée théorique concernant le problème des infinis date de 1947. Cette année-là furent en effet mesurés précisément certains écarts dans les structure fine et hyperfine des niveaux d'énergie de l'atome d'hydrogène, écarts par rapport aux prédictions de l'équation de Dirac d'un électron dans le champ coulombien du proton.

L'un de ces écarts est le célèbre décalage de Lamb (Lamb shift). Ce résultat expérimental fut discuté intensément du 2 au 4 Juin 1947 lors de le « conférence de Shelter Island » de physique théorique intitulée : « Les fondements de la mécanique quantique ».

À l'issue de cette conférence, dans un train qui l'emmenait de New-York à Schenectady^[7], le théoricien Bethe réussit pour la première fois à calculer un ordre de grandeur fini correct de ce déplacement de Lamb. Mais ce premier calcul était non-relativiste, donc imparfait. De retour début Juillet à l'université Cornell (Ithaca) où il enseignait, Bethe fit une conférence au cours de laquelle il exposa son résultat, concluant qu'un calcul entièrement relativiste était nécessaire. Dans l'assistance figurait le jeune Feynman, qui vint voir Bethe à la fin de l'exposé pour lui dire qu'il pensait pouvoir faire ce calcul relativiste. Ce qu'il fit.

La difficulté des infinis ne fut cependant entièrement surmontée qu'en 1948, avec l'invention de la procédure systématique de renormalisation, due principalement aux travaux du japonais Tomonaga et des américains Schwinger (Université Harvard) et Feynman. Ces trois auteurs se partageront le prix Nobel de physique 1965. L'équivalence de la formulation abstraite développée par Schwinger et de celle, basée sur des graphes, inventée indépendamment par Feynman, fut démontrée en 1948 par Dyson (Institute for Advanced Study, Princeton).

La méthode de quantification du champ électromagnétique proposée par Feynman est basée sur son concept d'intégrale de chemin. L'utilisation systématique de cette procédure de quantification à la place de la vieille quantification canonique permettra ultérieurement une quantification aisée des théories de jauge.

Théories de jauge

Les succès de l'électrodynamique quantique, théorie de jauge Abélienne basée sur le groupe commutatif U(1), a conduit les théoriciens à appliquer les concepts de la théorie quantique des champs aux théories de jauge non-Abéliennes. Ces théories sont également appelées théories de Yang-Mills, d'après le nom de leurs deux inventeurs en 1954 : Chen Yang et Robert Mills. L'utilisation de ces théories a donné naissance à l'actuel modèle standard de la physique des particules.

La première théorie fut la théorie unifiée électro-faible de Glashow, Salam et Weinberg (1962-1968), construite sur le groupe de jauge 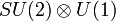. Ces auteurs ont reçu le prix Nobel de physique 1979. Dans cette théorie, les particules matérielles (électrons, muons, neutrinos...) interagissent en échangeant un ou plusieurs bosons virtuels : photon, W⁺, W^- et Z⁰. À la différence du photon, les bosons-vecteurs W et Z sont massifs, leur masse étant de l'ordre de 100 GeV/c². Ceci explique la très courte portée de l'interaction faible. L'introduction d'une masse pour ces particules a d'ailleurs nécessité l'invention d'un mécanisme nouveau, appelé mécanisme de Higgs (du nom de son inventeur Peter Higgs), car l'introduction d'un terme de masse classique dans le Lagrangien briserait l'invariance de jauge. Ce mécanisme, la brisure spontanée de symétrie, a été introduit par Higgs. Il lui correspond une nouvelle particule massive, le boson de Higgs, non encore mise en évidence expérimentalement mais dont la vérification finale devrait avoir lieu avec la mise en route prochaine du LHC (2007 en principe).

Vint ensuite dans les années 1970 la théorie de l'interaction nucléaire forte, élaborée par Gross, Politzer et Wilczek; ces trois auteurs ont obtenu le prix Nobel de physique 2004. Cette théorie, également baptisée chromodynamique quantique (Q.C.D.), est bâtie sur le groupe de jauge SU(3) de couleur. Les particules matérielles (quarks) y interagissent en échangeant un ou plusieurs bosons virtuels, les gluons. Comme le photon, les gluons sont des particules de masse nulle. Mais, à la différence du photon, les gluons portent une charge de couleur et interagissent entre-eux : contrairement à l'électrodynamique de Maxwell, les théories de Yang-Mills sont en effet non-linéaires. Une autre propriété remarquable de la chromodynamique quantique a été celle de la liberté asymptotique c'est-à-dire le fait pour les quarks de voir leur interaction faiblir lorsque les énergies mises en jeu sont très grandes et au contraire d'interagir très fortement à faible énergie. Ce phénomène particulier est à l'origine du mécanisme de confinement des quarks qui empêche d'observer un quark à dans un état isolé. En effet, si on augmente la distance entre deux quarks leur énergie d'interaction devient si grande que d'autres quarks surgissent du vide environnant de sorte que la charge de couleur observée de loin reste toujours nulle.

Une étape décisive dans la validation de ces théories de jauge non-Abéliennes a été la preuve de leur renormalisabilité, établie en 1972 par 't Hooft et Veltman, prix Nobel de physique 1999.

Physique statistique

Le programme de la physique statistique est de décrire les propriétés macroscopiques des corps à partir de leur contenu microscopique. Un problème important consiste en particulier à décrire les changements d'état, appelés également transitions de phase. Dans certaines conditions expérimentales, certains corps présentent parfois un comportement particulier qu'on range sous l'appellation de phénomène critique, qui sont caractérisés par certains exposants critiques universels. Le calcul de ces exposants critiques par les anciennes méthodes de la physique statistique (méthodes de champ moyen) donnaient des résultats en désaccord avec l'expérience.

À la fin des années 1960, Kadanoff avait introduit l'idée que les transitions de phase présentaient des propriétés d'universalité et d'invariance d'échelle. Wilson eut alors l'idée d'appliquer les méthodes de renormalisation de la théorie quantique des champs. Les succès de cette nouvelle approche ont valu à Wilson le prix Nobel de physique 1982; les spécialistes —Wilson le premier— ont été surpris que Kadanoff n'ait pas été associé à cette prestigieuse reconnaissance.

Pour sa part, la France a contribué de façon significative à cette aventure de calculs d'exposants critiques, avec les travaux réalisés dans les années 1970 par Jean Zinn-Justin (Service de physique théorique du C.É.A., Saclay), Jean-Claude Le Guillou (Laboratoire de physique théorique et hautes énergies, Université Paris 6) et Édouard Brézin (Laboratoire de physique théorique de l'E.N.S.).

Annexes

Article connexe

• Frise chronologique de la physique microscopique

Bibliographie

Études d'ensemble

• José Leite-Lopes & Bruno Escoubès ; Sources et évolution de la physique quantique - Textes fondateurs, Masson (1995) [ISBN 2-225-84607-3]. Réédité par E.D.P. Sciences. Donne une vue générale de l'évolution des idées, du XIXe siècle à 1993.
• Olivier Darrigol ; La genèse du concept de champ quantique, Annales de Physique (France) 9 (1984) 433-501. Étude érudite qui couvre la première période 1925-1940.
• Abraham Pais ; Inward Bound - Of Matter & Forces in the Physical World, Oxford University Press (1986) [ISBN 0-19-851997-4] Écrite par un ancien assistant d'Einstein à Princeton, cette superbe histoire des développements de la physique moderne démarre en 1895 avec la découverte expérimentale des rayons X, et se termine en 1983 lors de la découverte expérimentale au C.E.R.N. des bosons-vecteurs W et Z. L'auteur décrit avec beaucoup de détails l'évolution des idées, indiquant systématiquement les références des publications originales. Quel dommage que ce livre ne soit pas traduit en français...
• Emilio Segré ; Les physiciens modernes et leurs découvertes - Des rayons X aux quarks, Fayard (1984) [ISBN 2-213-01383-7]. Une histoire vulgarisée qui couvre la même période que le livre précédent. L'auteur a reçu le prix Nobel de physique 1959 pour la découverte expérimentale de l'antiproton.
• Steven Weinberg ; The Quantum Theory of Fields - Foundations (vol. I), Cambridge University Press (1995) [ISBN 0-521-55001-7] Le premier chapitre (pp. 1-40) du traité monumental de Weinberg contient une brève histoire de la théorie quantique des champs.
• Silvian S. Schweber ; Q.E.D. and the men who made it: Dyson, Feynman, Schwinger, and Tomonaga, Princeton University Press (1994) [ISBN 0-691-03327-7]
• Arthur I. Miller (ed) ; Early Quantum Electrodynamics : A Sourcebook, Cambridge University Press (1995) [ISBN 0521568919]
• Julian Schwinger (ed) ; Selected Papers on Quantum Electrodynamics, Dover Publications, Inc. (1958) [ISBN 0-486-60444-6]
• Lochlainn O'Raifeartaigh ; The Dawning of Gauge Theory, Princeton University Press (May 5, 1997) [ISBN 0-69-102977-6]
• Tian Yu Cao ; Conceptual Developpments of 20th Century Field Theories, Cambridge University Press (1997) [ISBN 0-521-63420-2]
• Andrew Pickering ; Constructing quarks - A sociological history of particle physics, The University of Chicago Press (1984) [ISBN 0-226-66799-5]. Une histoire qui couvre la période allant des années 1960 (modèle des quarks de Gell-Mann et Low) à 1983 (découverte expérimentale des bosons-vecteurs).
• Tian Yu Cao ; A History of Q.C.D., à paraître.

Références historiques

• Paul Adrien Maurice Dirac ; The quantum theory of the emission and absorption of radiation, Proceedings of the royal society A114 (1927) 243-265. Republié dans : Julian Schwinger (ed) ; Selected Papers on Quantum Electrodynamics, Dover Publications, Inc. (1958) [ISBN 0-486-60444-6]
• Niels Bohr et Léon Rosenfeld ; Zur frage der messbarkeit der electromagnetischen feldgrossen, Kgl. Danske Vidensk. Selskab. Mat.-Fys. Medd. 12 (1933) 8. Voir également : Niels Bohr et Léon Rosenfeld ; Field and Charge Measurements in Quantum Electrodynamics, Physical Review 78 (1950) 794.

Références

• Portail de la physique