Groupe de frobenius

En mathématiques, un groupe de Frobenius est un groupe de permutation transitif sur un ensemble fini, tel qu'aucun élément non-trivial ne fixe plus d'un point et tel qu'un certain élément fixe un point. Ils ont été nommés en l'honneur de F. G. Frobenius.

Sommaire 1 Structure 2 Exemples 3 Théorie de la représentation 4 Références

Structure

Le sous-groupe H d'un groupe de Frobenius G fixant un point de l'ensemble X est appelé le complément de Frobenius. L'élément neutre en même temps que tous les éléments différent de n'importe quel conjugué de H forme un sous-groupe normal appelé le noyau de Frobenius K. (Ceci est un théorème dû à Frobenius.) Le groupe de Frobenius G est le produit semi-direct de K et H:

G = K ⋊ H.

Le noyau de Frobenius et le complément de Frobenius ont tous deux des structures très restreintes. J. G. Thompson a démontré que le noyau de Frobenius K est un groupe nilpotent. Si H est d'ordre pair alors K est abélien. Le complément de Frobenius H possède la propriété que chaque sous-groupe dont l'ordre est le produit de 2 nombres premiers est cyclique; ceci implique que ses sous-groupes de Sylow sont cycliques ou des groupes de quaternions généralisés. Tout groupe tel que tous ses sous-groupes sont cycliques est métacyclique : ceci signifie que c'est l'extension de deux groupes cycliques. Si un complément de Frobenius H est non résoluble alors Zassenhaus a montré qu'il possède un sous-groupe normal d'index 1 ou 2, c’est-à-dire le produit de SL2(5) et le groupe métacyclique d'ordre premier avec 30. Si un complément de Frobenius H est résoluble alors il possède un sous-groupe normal métacyclique tel que le quotient est un sous-groupe du groupe symétrique à 4 points.

Le noyau de Frobenius K est uniquement déterminé par G comme il est le sous-groupe de Fitting et le complément de Frobenius est uniquement déterminé jusqu'au conjugué par le théorème de Schur-Zassenhaus. En particulier, un groupe fini G est un groupe de Frobenius d'au plus une manière.

Exemples

• Le plus petit exemple est le groupe symétrique à 3 points, avec 6 éléments. Le noyau de Frobenius K est d'ordre 3 et le complément H est d'ordre 2.

• Pour chaque corps fini F_q avec q (> 2) éléments, le groupe des transformations affines inversibles 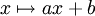, 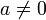avec son action naturelle sur F_q est un groupe de Frobenius. L'exemple précédent correspond au cas F₃, le corps à trois éléments.

• Plus généralement, le groupe des matrices triangulaires supérieures 2 x 2 inversibles de déterminant 1 sur n'importe quel corps fini d'ordre au moins 3 est un groupe de Frobenius. Le noyau de Frobenius est le sous-groupe des matrices triangulaires strictement supérieures (avec les éléments diagonaux égaux à 1), et le complément est le sous-groupe des matrices diagonales.

• Le groupe dihédral d'ordre 2n avec n impair est un groupe de Frobenius avec un complément d'ordre 2. Plus généralement, si K est un groupe abélien quelconque d'ordre impair et H est d'ordre 2 et agit sur K par inversion, alors le produit semi-direct K.H est un groupe de Frobenius.

• Beaucoup d'exemples avancés peuvent être engendrés par les constructions suivantes. Si nous remplaçons le complément de Frobenius d'un groupe de Frobenius par un sous-groupe non-trivial, nous obtenons un autre groupe de Frobenius. Si nous avons deux groupes de Frobenius K₁.H et K₂.H alors (K₁ × K₂).H est aussi un groupe de Frobenius.

• Si K est le groupe non-abélien d'ordre 7³ avec l'exposant 7, et H est le groupe cyclique d'ordre 3, alors il existe un groupe de Frobenius G qui est une extension K.H de H par K. Ceci donne un exemple d'un groupe de Frobenius avec un noyau non-abélien.

• Si H est le groupe SL₂(F₅) d'ordre 120, il agit sur le point fixé librement sur un espace vectoriel à 2 dimensions K sur le corps à 11 éléments. L'extension K.H est le plus petit exemple d'un groupe de Frobenius non-résoluble.

• Le sous-groupe d'un groupe de Zassenhaus fixant un point est un groupe de Frobenius.

Théorie de la représentation

Les représentations complexes irréductibles d'un groupe de Frobenius G peuvent être lu éloignés de H et K. Il existe deux types de représentations irréductibles de G :

• Toute représentation irréductible R de H donne une représentation irréductible de G utilisant l'application quotient de G vers H (c’est-à-dire, comme une représentation restreinte). Ceux-ci donnent les représentations irréductibles de G avec K dans leurs noyaux.
• Si S est une représentation irréductible non-triviale quelconque de K, alors la représentation induite correspondante de G est aussi irréductible. Ceux-ci donnent les représentations irréductibles de G avec K qui ne sont pas dans leurs noyaux.

Références

• D. S. Passman, Permutation groups, Benjamin 1968

• Portail des mathématiques