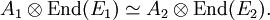Algebre d'Azumaya

Algebre d'Azumaya

Algèbre d'Azumaya

En mathématiques, la notion d'algèbre d'Azumaya est une généralisation de la notion d'algèbre centrale simple aux R-algèbres dont les scalaires R ne forment pas un corps. Elle a été introduite dans un article de Goro Azumaya en 1951, dans le cas où R est un anneau local commutatif, puis a été développée par Alexander Grothendieck comme ingrédient de base à une théorie du groupe de Brauer en géométrie algébrique, dans les séminaires Bourbaki à partir de 1964.

Dans le cas où R est un anneau local, une algèbre d'Azumaya A est une R-algèbre libre et de rang fini r, telle que son produit tensoriel avec son algèbre opposée soit isomorphe à une l'algèbre de matrices carrées de taille r sur R.

Du point de vue de la théorie des schémas, Grothendieck la définit comme un faisceau A de OX-algèbres (où X est un schéma, et OX son faisceau structurel) localement isomorphe à un faisceau d'algèbres de matrices. Milne prend en revanche la définition selon laquelle les fibres Ax sont des algèbres d'Azumaya sur les anneaux locaux OX,x en tout point x.Le groupe de Brauer est alors définit comme l'ensemble des classes d'équivalence d'algèbres d'Azumaya selon la relation : deux algèbres A1 et A2 sont équivalentes s'il existe des faisceaux localement libres E1 et E2 tels que :

A_1\otimes\mathrm{End}(E_1) \simeq A_2\otimes\mathrm{End}(E_2).

Une structure de groupe est obtenue à partir du produit tensoriel, l'opposé étant donné par l'algèbre opposée.

Cette notion a des applications en géométrie arithmétique, notamment grâce au travail de Yuri Manin sur les obstructions au principe de Hasse.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Alg%C3%A8bre d%27Azumaya ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Algebre d'Azumaya de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Algèbre d'Azumaya — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, la notion d algèbre d Azumaya est une généralisation de la notion d algèbre centrale simple aux R algèbres dont les scalaires R ne forment pas un corps. Elle a été… …   Wikipédia en Français

  • Algèbre (homonymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le mot « algèbre » vient de l arabe ’al ǧabr (« réduction »), désignant une technique de chirurgie des membres puis une technique de… …   Wikipédia en Français

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Yuri Manin — Pour les articles homonymes, voir Manin (homonymie). Yuri Manin à l ICM de Madrid en 2006, à côté de Ksenia Semenova Yuri Ivanovitch Manin …   Wikipédia en Français

  • Groupe De Brauer — En mathématiques, le groupe de Brauer constitue l espace classifiant des algèbres centrales simples sur un corps commutatif k donné, pour une certaine relation d équivalence. On munit cet espace d une structure de groupe abélien en l identifiant… …   Wikipédia en Français

  • Groupe de Brauer — En mathématiques, le groupe de Brauer constitue l espace classifiant des algèbres centrales simples sur un corps commutatif k donné, pour une certaine relation d équivalence. On munit cet espace d une structure de groupe abélien en l identifiant… …   Wikipédia en Français

  • Groupe de brauer — En mathématiques, le groupe de Brauer constitue l espace classifiant des algèbres centrales simples sur un corps commutatif k donné, pour une certaine relation d équivalence. On munit cet espace d une structure de groupe abélien en l identifiant… …   Wikipédia en Français

  • Lemme de Nakayama — Le lemme de Nakayama est un résultat fondamental d algèbre commutative. Il doit son origine à T. Nakayama, G. Azumaya et Wolfgang Krull. Sommaire 1 Énoncés 2 Démonstrations 2.1 Cas particulier 2 …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”