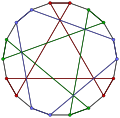
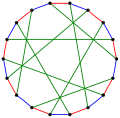
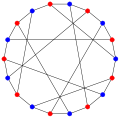
- Graphe de Pappus
-
Graphe de Pappus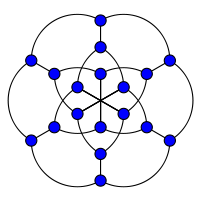 
Le graphe de PappusNombre de sommets 18 Nombre d'arêtes 27 Distribution des degrés 3-régulier Rayon 4 Diamètre 4 Maille 6 Automorphismes 216 Nombre chromatique 2 Indice chromatique 3 Propriétés Hamiltonien
Cubique
Symétriquemodifier 
En théorie des graphes, le graphe de Pappus est un graphe cubique symétrique possédant 18 sommets et 27 arêtes[1]. Il doit son nom à Pappus d'Alexandrie, un mathématicien du IVe siècle. C'est le graphe d'incidence de la configuration apparaissant dans le théorème de Pappus.
Sommaire
Propriétés
Propriétés générales
Le graphe de Pappus est hamiltonien et possède 72 cycles hamiltonien distincts.
Le diamètre du graphe de Pappus, l'excentricité maximale de ses sommets, est 4, son rayon, l'excentricité minimale de ses sommets, est 4 et sa maille, la longueur de son plus court cycle, est 6. Il s'agit d'un graphe 3-sommet-connexe et d'un graphe 3-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 3 sommets ou de 3 arêtes.
Le graphe de Pappus n'est pas planaire. En fait, pour le dessiner sur un plan, il faut nécessairement que plusieurs arêtes se croisent. Il est possible de le dessiner avec seulement 5 croisements et ce nombre est minimal[2]. Avec ses 18 sommets, il est le plus petit graphe cubique nécessitant 5 croisements pour être dessiné sur le plan[3].
Coloriage
Le nombre chromatique du graphe de Pappus est 2. C'est-à-dire qu'il est possible de le colorer avec 2 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 1-coloration valide du graphe.
L'indice chromatique du graphe de Pappus est 3. Il existe donc une 3-coloration des arêtes du graphe telles que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Il est possible de compter les colorations distinctes d'un graphe. Cela donne une fonction dépendant du nombre de couleurs autorisées. Cette fonction est polynomiale et est qualifiée de polynôme chromatique du graphe. Ce polynôme a pour racines tous les entiers positifs ou nuls strictement inférieurs à 2 et est de degré 18. Il est égal à : (x − 1)x(x16 − 26x15 + 325x14 − 2600x13 + 14950x12 − 65762x11 + 229852x10 − 653966x9 + 1537363x8 − 3008720x7 + 4904386x6 − 6609926x5 + 7238770x4 − 6236975x3 + 3989074x2 − 1690406x + 356509).
Propriétés algébriques
Le graphe de Pappus est symétrique, c'est-à-dire que son groupe d'automorphisme agit transitivement sur ses arêtes, ses sommets et ses arcs. Son groupe d'automorphisme est d'ordre 216. C'est l'unique graphe cubique symétrique à 18 sommets et sa notation dans le Foster Census est F18A[4],[5].
Le polynôme caractéristique du graphe de Pappus est : (x − 3)x4(x + 3)(x2 − 3)6.
Galerie
-
Le graphe de Pappus coloré de façon à mettre en valeur certains de ses 6-cycles.
-
L'indice chromatique du graphe de Pappus est~3.
-
Le nombre chromatique du graphe de Pappus est~2.
Références
- (en) Weisstein, Eric W. "Pappus Graph" From MathWorld--A Wolfram Web Resource
- (en) Weisstein, Eric W. "Graph Crossing Number" From MathWorld--A Wolfram Web Resource
- (en) Pegg, E. T. and Exoo, G. "Crossing Number Graphs." Mathematica J. 11, 2009
- (en) Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41-63, 2002
- (en) Royle, G. "Cubic Symmetric Graphs (The Foster Census)."
Catégorie :- Graphe remarquable
-
Wikimedia Foundation. 2010.
