- Graphe complet
-
Graphe complet 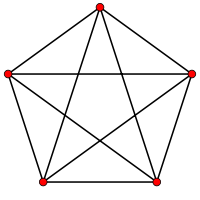
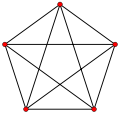
K5Notation Kn Nombre de sommets n Nombre d'arêtes n(n − 1) / 2 Distribution des degrés (n-1)-régulier Diamètre 1 Maille ∞ si n = 1 ou 2
3 si n > 2Nombre chromatique n Propriétés Hamiltonien, symétrique, régulier modifier 
En théorie des graphes, le graphe complet Kn est l'unique graphe à isomorphisme près possédant n sommets tous reliés deux à deux par une arête.
Dans un graphe G quelconque, on appelle clique un sous-ensemble de sommets induisant un sous-graphe complet de G. Rechercher une clique de taille maximum dans un graphe est un problème classique en théorie des graphes. Il est NP-complet.
Le graphe K5 est le plus petit graphe non planaire. Il sert dans les caractérisations des graphes planaires de Kazimierz Kuratowski et de Klaus Wagner.
La notion de graphe biparti complet existe également. Mais un graphe biparti complet n'est pas un graphe complet.
Propriétés
Le nombre d'arêtes de Kn est :
 .
.
Le premier terme s'obtient en remarquant que la suppression d'un premier sommet de Kn entraine la suppression de n − 1 arêtes, la suppression d'un deuxième sommet, la suppression de n − 2 arêtes, et celle d'un i-ème sommet n − i arêtes. Le deuxième terme s'obtient par la même opération en marquant les arêtes au lieu de les supprimer, chaque arête est alors marquée deux fois et l'on fait n − 1 marquages par sommet (c'est la formule générale de la demi-somme des degrés).
Le graphe complet Kn est symétrique : il est sommet-transitifs, arête-transitif et arc-transitif. Cela signifie que son groupe d'automorphismes agit transitivement sur l'ensemble de ses sommets, de ses arêtes et de ses arcs. Ce groupe d'automorphismes est de cardinal n! et est isomorphe au groupe symétrique Sn.
Galerie
Pour chacun des graphes complets de 1 à 12 sommets, est indiqué le nombre de ses arêtes.
-
K1 : 0 arête
graphe singleton -
K3 : 3 arêtes
graphe triangle -
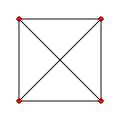
K4 : 6 arêtes
graphe tétraédrique
Catégorie :- Famille de graphes
Wikimedia Foundation. 2010.