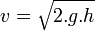- Formule de torricelli
-
Formule de Torricelli
La formule de Torricelli est une formule d'hydrodynamique des fluides parfaits, qui exprime la conservation de l'énergie. Cette formule a été énoncée par Torricelli dans 'De Motu Aquarum qui fait partie du traité de 1644, Opera Geometrica.
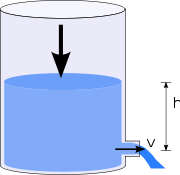
- Dans un vase contenant un fluide parfait, d'un trou pratiqué à la hauteur h en-dessous de la surface horizontale, le liquide s'écoule avec une vitesse v
- avec g l'accélération de la pesanteur.
Une conséquence immédiate est que la vitesse est indépendante de la masse volumique du liquide considéré. Le mercure ou bien l'eau s'écoulent donc à la même vitesse. On retrouve ainsi la loi de Galilée sur la chute libre des corps translatée en hydrodynamique.
Une autre conséquence de la formule de Torricelli est que plus la hauteur de liquide est importante, plus la vitesse d'éjection est élevée.
Sommaire
Démonstration
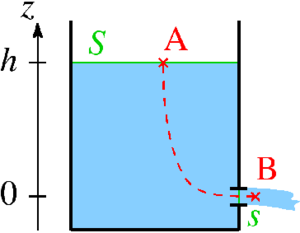
On considère une cuve remplie d'un liquide parfait et incompressible, dans laquelle a été percé un trou de petite taille à une hauteur h en dessous de la surface libre du liquide. On note A un point choisi au hasard sur la surface libre du liquide et B un point pris au niveau du jet libre généré par le trou.
On suppose que le trou est assez petit pour que :
- le diamètre du trou soit négligeable devant la hauteur h de liquide au dessus du trou, de manière à ce que h puisse être considéré comme constant au niveau du trou ;
- la surface s du trou soit négligeable devant la surface libre S du liquide ; la conservation du débit impose que vAS = vBs, d'où
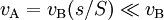; on peut donc considérer que la hauteur h ne varie pas au cours du temps, et que l'écoulement du liquide est permanent.
L'ensemble du liquide participant à l'écoulement, on peut relier les points A et B au travers d'une ligne de courant.
En admettant enfin que le champ de pesanteur est uniforme à l'échelle de la cuve, il est alors possible d'appliquer le théorème de Bernoulli au niveau des points A et B :
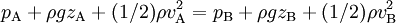.Or la pression au niveau de la surface libre du liquide pA et la pression au niveau du jet libre pB sont toutes deux égales à la pression atmosphérique p0, et d'autre part on peut négliger la vitesse du liquide au point A : vA = 0.
On en déduit l'expression de la vitesse du liquide au point B :
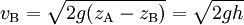.En considérant les différentes hypothèses nécessaires à l'établissement de cette formule, l'analogie avec la chute libre doit être interprétée avec précaution.
Remarque : La loi de Bernoulli n'avait pas encore été énoncée à l'époque où Torricelli propose cette loi. Cette démonstration n'est donc pas celle qui a pu le conduire au résultat.
Torricelli est-il l'auteur de la loi qui porte son nom ?
Plus la hauteur de liquide est importante, plus la vitesse est grande- Antérieurement à la publication des travaux de Torricelli, Mersenne a écrit de nombreuses lettres à Peiresc en 1634. En 1639, il semble que Descartes le félicite pour sa loi qui calque « par anticipation » celle de Torricelli. Ces écrits sont conservés aux Arts et Métiers à Paris.
- Descartes, Mersenne, Gassendi écrivent beaucoup jusqu'en 1643 et après. Les difficultés sont bien cernées : niveau d'eau constant, perte de charge si rétrécissement, problème de la buse de sortie, et bien évidemment le jet d'eau et la loi de 1638 de Galilée (4e journée). Hydraulica de Mersenne paraît en 1644 et Mersenne rencontra Torricelli en 1645. Clairement, si les vases communicants font remonter l'eau au niveau du lac, il est manifeste que le jet d'eau dirigé verticalement n'y remonte pas vraiment, et chacun voit bien ce que produit la modification de la buse dans un jet d'arrosage. La démonstration manifestement dépasse les physiciens de l'époque.
- Postérieurement, 1668, à l'Académie des Sciences de Paris, Christiaan Huygens et Jean Picard, puis Edme Mariotte reprennent le problème.
En 1695, donc après Newton (1687), Pierre Varignon raisonne ainsi :
- « La petite masse d'eau ρ.S.dx est éjectée par la force de pression S.ρ.g.h avec une quantité de mouvement ρ.S.dx.v pendant le temps dt : soit v² = g.h »
mais il y manque toujours le facteur 2.
En 1738, Daniel Bernoulli donne enfin la solution dans son Hydrodynamica. Leonhard Euler viendrait bientôt : tout deviendrait clair. Cette loi a donc fait couler beaucoup... d'eau.
Voir aussi
Liens externes
Catégorie : Mécanique des fluides - Dans un vase contenant un fluide parfait, d'un trou pratiqué à la hauteur h en-dessous de la surface horizontale, le liquide s'écoule avec une vitesse v
Wikimedia Foundation. 2010.
