- Force Centrale
-
Force centrale
En mécanique classique du point matériel, un champ de forces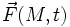 est dit champ de force centrale, s'il vérifie les trois conditions suivantes :
est dit champ de force centrale, s'il vérifie les trois conditions suivantes :- Il est indépendant du temps, donc
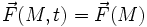
- Il est dirigé (centripète ou centrifuge) en direction du centre de force O, donc
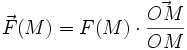
- F(M) = F(r,θ,φ) ne dépend que de la distance radiale r = OM (pas de la colatitude θ,ni de la longitudeφ) : F(M) = F(r).
On note souvent
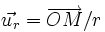 , le vecteur unitaire radial centrifuge.
, le vecteur unitaire radial centrifuge.
Finalement, la force centrale s'écrit algébriquement :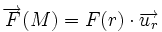 .
.On montre assez facilement qu'on peut lui associer une énergie potentielle (scalaire), notée
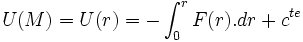 . Souvent la constante est choisie conventionnellement, si cela est possible, pour que
. Souvent la constante est choisie conventionnellement, si cela est possible, pour que 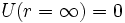 .
.Sommaire
La force linéaire de Hooke
Robert Hooke (1635-1703) dans sa correspondance de novembre et décembre 1679 avec Isaac Newton, à énoncer la loi de ce champ de force centripète. Pour l'anecdote, durant tout l’hiver 1679/1680, Robert Hooke avait engagé une correspondance avec Newton. De cette correspondance naissait en 1684 le manuscrit "de Motu corporum gyrum", que l’on peut assimiler au germe des "Principia". Notons que Newton n’y fera aucune mention de sa "collaboration" avec R. Hooke. Dans un manuscrit de 1685, Robert Hooke propose une méthode de calcul des orbites qu’il applique avec succès au calcul du mouvement d’un pendule conique (figure de sept 1685 - manuscrits Trinity college) :
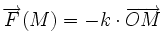
Le coefficient k est dit constante de rappel du ressort (ou également : raideur du ressort); k s'exprime en N/m.
L'énergie potentielle associée est conventionnellement prise égale à
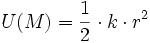 .
.Hooke considéra le mouvement du pendule sphérique pour de très petites oscillations, comme dû au mouvement de la petite masse sous l'action d'un champ central
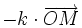 avec
avec 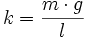 , l étant le rayon de la sphère.
, l étant le rayon de la sphère.Il généralisait ainsi le travail de Galilée sur le pendule simple (1601). L'observation en est très aisée car la trajectoire est une simple ellipse ayant pour centre le point O (en France, on parle d'ellipse de Lissajous, mais il s'agit plus correctement d'ellipse de Galilée-Hooke).
Remarque: si les oscillations ne sont pas très petites, il s'agit du pendule sphérique, beaucoup plus difficile à étudier.
Le champ newtonien
Isaac Newton démontra en 1685 le théorème dit de Newton-Gauss (voir Théorème de Gauss appliqué à l'électrostatique) :
la loi universelle d'attraction gravitationnelle entre un astre sphérique, de centre O, de masse M et de rayon R, sur une petite masse ponctuelle m située en M, extérieur à la sphère ( donc r = OM > R) se réduit à la simple force centrale
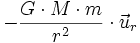 .
.Ce théorème est tout à fait remarquable et a profondément étonné Newton, qui le considéra comme une de ses principales découvertes.
Le mouvement des planètes, sous l'action du champ newtonien du Soleil ,
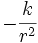 , où
, où 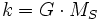 est la constante de Gauss, connue avec une précision remarquable (10 chiffres significatifs), est celui décrit par les célèbres lois de Kepler, démontrées en 1684 par Newton dans le « de Motu », qui fut réécrit, (dès que Newton eut claire conscience du théorème de Newton-Gauss au travers de la loi universelle de la gravitation), en un traité non moins célèbre : les Principia (voir Démonstration des lois de Kepler).
est la constante de Gauss, connue avec une précision remarquable (10 chiffres significatifs), est celui décrit par les célèbres lois de Kepler, démontrées en 1684 par Newton dans le « de Motu », qui fut réécrit, (dès que Newton eut claire conscience du théorème de Newton-Gauss au travers de la loi universelle de la gravitation), en un traité non moins célèbre : les Principia (voir Démonstration des lois de Kepler).Grâce à ce théorème, Newton réunifiait les deux mondes,celui de Galilée et celui de Kepler : la mécanique terrestre et la mécanique céleste (voir les Dialogues de Galilée).
Le champ newtonien a pour énergie potentielle,
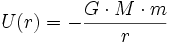 (à laquelle il faut rajouter une constante qui est nulle par convention), soit au niveau de la Terre
(à laquelle il faut rajouter une constante qui est nulle par convention), soit au niveau de la Terre 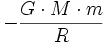 . Il faut donc donner à un projectile l'énergie cinétique initiale opposée pour qu'il puisse s'extraire du champ de pesanteur : la vitesse correspondante, de l'ordre de 11,186 km/s, est la deuxième vitesse cosmique (second space velocity) :
. Il faut donc donner à un projectile l'énergie cinétique initiale opposée pour qu'il puisse s'extraire du champ de pesanteur : la vitesse correspondante, de l'ordre de 11,186 km/s, est la deuxième vitesse cosmique (second space velocity) : 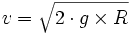 , indépendante de m (loi de Galilée : masse inerte et masse-charge gravitationnelle sont toujours proportionnelles et donc, si on choisit les mêmes unités, sont identiques. Cette loi, élevée au rang de Principe d'équivalence sera le point d'ancrage de la Théorie de la Gravitation d'Einstein. Ce Principe doit être vérifié expérimentalement par le satellite "micron".
, indépendante de m (loi de Galilée : masse inerte et masse-charge gravitationnelle sont toujours proportionnelles et donc, si on choisit les mêmes unités, sont identiques. Cette loi, élevée au rang de Principe d'équivalence sera le point d'ancrage de la Théorie de la Gravitation d'Einstein. Ce Principe doit être vérifié expérimentalement par le satellite "micron".L'étude générale du champ newtonien fait l'objet, en sciences de la Terre , de la gravimétrie; en électrostatique, du champ des charges fixes portées par des isolants; en mathématiques, de la théorie du potentiel, sujet très développé par Henri Poincaré et Ito et Doob.
Épistémologie et histoire des sciences
En effet, on en déduit immédiatement que pour la Terre, de masse MT , considérée comme sphérique, la gravité terrestre g est
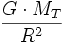 ; et que pour la Lune, « considérée comme une pomme » éloignée de soixante rayons terrestres, l'influence de la Terre est (60)2 = 3600 fois plus petite : ce calcul, est resté célèbre à juste titre, et fit la renommée de Newton. Afin de se rendre compte de la simplicité du résultat, on cite Newton lui-même, souriant:
; et que pour la Lune, « considérée comme une pomme » éloignée de soixante rayons terrestres, l'influence de la Terre est (60)2 = 3600 fois plus petite : ce calcul, est resté célèbre à juste titre, et fit la renommée de Newton. Afin de se rendre compte de la simplicité du résultat, on cite Newton lui-même, souriant:Soit une pomme, au dessus de ma tête : elle est attirée à gauche par l'hémisphère terrestre gauche, de masse M/2,par une force difficile à calculer, dirigée vers un point C1, qui n'est pas le centre de gravité de l'hémisphère, et symétriquement elle est attirée à droite par l'autre hémisphère, de masse M/2, vers un point C2. Par symétrie, ces deux forces se composent en une force dirigée vers le centre O de la Terre (et la pomme me tombe dessus), mais il est incroyablement simple que la loi soit en 1/OM².
(Or Newton ne souriait quasiment jamais ! Cette anecdote, patrimoine de la physique, est appelée dans le monde entier, the Newton's apple : elle est malheureusement mal racontée; hélas, un peu comme le E= mc2 d'Einstein ou le Eurêka d'Archimède).En particulier , il en résulte cette conséquence immédiate, proprement invraisemblable, mais vite comprise par Newton: pour une coque massique sphérique de masse M, de rayon interne R1, de rayon externe R2, la gravité externe est
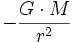 , MAIS la gravité interieure est rigoureusement nulle : tout objet y flotte en apesanteur (il s'agit bien ici d'apesanteur et non d'impesanteur). Le Théorème d'Ivory généralise ce fait extraordinaire d'apesanteur aux coques ellipsoïdales. Cavendish reprendra cela en électrostatique, voir expérience des hémisphères de Cavendish.
, MAIS la gravité interieure est rigoureusement nulle : tout objet y flotte en apesanteur (il s'agit bien ici d'apesanteur et non d'impesanteur). Le Théorème d'Ivory généralise ce fait extraordinaire d'apesanteur aux coques ellipsoïdales. Cavendish reprendra cela en électrostatique, voir expérience des hémisphères de Cavendish.Jules Verne s'amusa de ce phénomène curieux dans un de ses 80 romans.
Si près que l'on soit de la paroi interne de la coque, le mur tout proche attire autant que tout le reste de la coque dans l'autre sens, en un équilibre rigoureux nul, ceci de quelque manière que l'on définisse le « proche». À dire vrai, c'est cela le vrai théorème de Newton-Gauss, the extraordinary theorem : le théorème en 1/r² à l'extérieur, c'est de la broutille vite démontrée (et que d'ailleurs beaucoup ont intuité avant Newton. Cette intuition pour le cas externe était claire chez Newton depuis son raisonnement par similitude de 1671; mais il lui manquait l'intérieur de la Terre !). En ce sens, l'enseignement français pêche par grave négligence culturelle: les Principia ne sont pas sortis tout droit de la cuisse de Jupiter. Quant à savoir si Hooke possédait ce théorème étrange, il semble que cela soit encore un point discuté en histoire des sciences.
Par ailleurs, Newton, profondément pieux , était aussi très satisfait de ce théorème : si le système solaire était dans la coque interne d'un Univers sphérique, alors la partie droite de l'Univers équilibrait la force exercée par la partie gauche. Un Dieu unique pouvait régir cet Univers : pour Newton, l'espace et le temps purent être absolus d'entrée de jeu.
Pourtant, Galilée, Huygens et bien d'autres s'étaient attachés à démontrer le principe de la relativité galiléenne. L' œuvre magistrale de newton va étouffer l'équivalence des hypothèses. Même McLaurin qui essaiera de défendre le "principe du bateau" de Huygens ne sera pas suivi(1742). Il faudra attendre Fresnel, Michelson, puis Ernst Mach pour que ce principe de relativité retrouve un second souffle.
Champ en loi de puissance
Le champ est cette fois
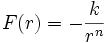 , donc l'énergie potentielle
, donc l'énergie potentielle 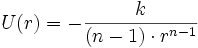 (exceptant n=1).
(exceptant n=1).Si n est négatif, on note généralement
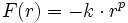 , d'énergie potentielle
, d'énergie potentielle 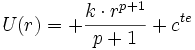 .
.De toute façon, l'énergie potentielle est croissante (si k est positif , certes) : on dit que la particule se meut dans un puits de potentiel.
On montre que, pour n<3,
si le moment cinétique
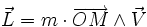 (constant) est non nul,
(constant) est non nul,la trajectoire reste bloquée entre un cercle péricentrique et un cercle apocentrique, dense dans la couronne sauf conditions initiales invraisemblables du point de vue physique.
Les deux cas d'exception sont ceux précités : n = 2 (Newton) et p = 1 (Hooke) : c'est le Théorème de Bertrand, car il y a dégénérescence : la période radiale est multiple de la période angulaire.
Lors de ce mouvement borné, l'énergie potentielle moyenne est f% .E°; E° étant l'énergie mécanique totale, et bien sûr la vitesse quadratique moyenne
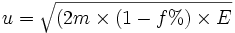 : c'est une forme du théorème du viriel.
: c'est une forme du théorème du viriel.Dans le cas où la vitesse initiale
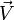 est rigoureusement perpendiculaire à la position initiale
est rigoureusement perpendiculaire à la position initiale 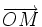 , la trajectoire est circulaire de rayon r tel que
, la trajectoire est circulaire de rayon r tel que 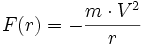 (cours de Terminale S).
(cours de Terminale S).Si une légère erreur se produit, la couronne est extrêmement étroite.
Ceci vaut pour toute loi centrale U(r), qui au voisinage de R peut se développer comme
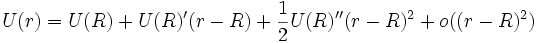 , ou bien comme U(r)#
, ou bien comme U(r)# 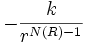 , où N(R) s'appelle l'indice local du champ. Le champ se « comporte comme » un champ en
, où N(R) s'appelle l'indice local du champ. Le champ se « comporte comme » un champ en 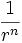 ),ou bien comme un champ d'indice N(R). Et un Théorème de Goursat et Levi-Civita, puis Bohlin, généralisé par Vladimir Arnold, montre que l'on peut ramener l'étude des champs d'indice p à ceux d'indice n ; ceci facilite l'étude (un peu fastidieuse) de tous les cas (la règle de correspondance involutive est (3+N)(3-p) = 4 ).
),ou bien comme un champ d'indice N(R). Et un Théorème de Goursat et Levi-Civita, puis Bohlin, généralisé par Vladimir Arnold, montre que l'on peut ramener l'étude des champs d'indice p à ceux d'indice n ; ceci facilite l'étude (un peu fastidieuse) de tous les cas (la règle de correspondance involutive est (3+N)(3-p) = 4 ).La solution est connue sous forme d'intégrales elliptiques ordinaires pour :
p = 5, 3, 1, 1/3 et n = 2, 3, 4, 5, 7 , 3/2 , 5/2, 5/3, 1/3.
Voir aussi
- Portail de la physique
Catégories : Article à désacadémiser | Mécanique classique - Il est indépendant du temps, donc
Wikimedia Foundation. 2010.
