- Force centrale en 1/r⁵
-
Force centrale en 1/r⁵
En physique, en mécanique classique, il s'agit d'un résultat établi par Isaac Newton, en corollaire de son exégèse des Principia Naturalis.Énoncé
Soit un point matériel P de masse m décrivant une trajectoire circulaire de rayon a et de centre C. On le soumet à l'attraction gravitationnelle d'un point O situé sur la circonférence de cette trajectoire circulaire.
On peut alors montrer que la loi de force centrale est en 1/OP⁵.
Démonstration historique
On note Q la position de P à t + dt. On note R l'intersection de la tangente en P et de la parallèle à OP passant par Q. D'après la seconde loi de Kepler, l'aire balayée pendant cet intervalle dt est constante, et égale ici à l'aire du triangle OPQ.
On calcule la limite du rapport 2RQ/(aire de OPQ)², selon l'expression fondamentale des Principia.
.
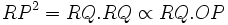D'autre part l'aire s'évalue par la podaire p comme : A(OPQ) = p.RP / 2, donc A(OPQ)² = p².RP ² / 4. On a alors
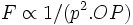. Or p = OP.sin(θ) et OP = 2a.sin(θ).Donc p.2a = OP², on obtient enfin
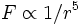.On peut également, avec les formules de Binet, obtenir le même résultat. Cette méthode était cependant inconnue du temps de Newton.
Voir aussi
- Force centrale ;
- Mouvement à force centrale ;
- Formules de Binet ;
- Exégèse des Principia ;
- Théorème de Sciacci.
Portail de la physique
Catégories : Article à désacadémiser | Mécanique classique
Wikimedia Foundation. 2010.
