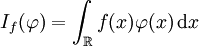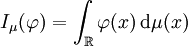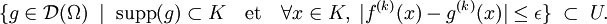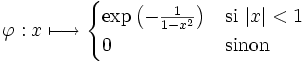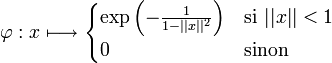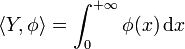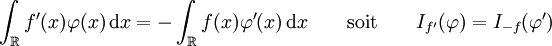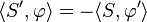Fonctions tests

Distribution (mathématiques)

Pour les articles homonymes, voir Distribution.

En analyse mathématique, une distribution (également appelée fonction généralisée) est un objet qui généralise la notion de fonction et de mesure. La théorie des distributions étend la notion de dérivée à toutes les fonctions localement intégrables et au-delà, et est utilisée pour formuler des solutions à certaines équations aux dérivées partielles. Elles sont importantes en physique et en ingénierie où beaucoup de problèmes discontinus conduisent naturellement à des équations différentielles dont les solutions sont des distributions plutôt que des fonctions ordinaires.

La théorie des distributions fut formalisée par le mathématicien français Laurent Schwartz et lui valut la médaille Fields en 1950. Son introduction utilise des notions d'algèbre linéaire et de topologie centrées autour de l'idée de dualité. Il faut chercher l'origine de cette théorie dans le calcul symbolique d'Heaviside (1894) et dans l'introduction par les physiciens de la « fonction de Dirac » (1926). L'objectif a été alors de généraliser la notion de fonction, afin de donner un sens mathématique correct à des objets manipulés par les physiciens. Il fallait en plus garder la possibilité de faire des opérations telles que des dérivations, convolutions, transformées de Fourier ou de Laplace.

La distribution de Dirac est un exemple intéressant de distribution car elle n'est pas une fonction, mais peut être représentée de façon informelle par une fonction dégénérée qui serait nulle sur tout son domaine de définition sauf en 0 et dont l'intégrale vaudrait 1. En réalité, de manière tout à fait stricte, elle est la limite au sens des distributions d'une suite de fonctions d'intégrale 1 et convergeant uniformément vers 0 sur tout compact ne contenant pas 0. Un tel objet mathématique est utile en physique ou en traitement du signal, mais aucune fonction ordinaire n'a ces propriétés.

Idées de bases

On évalue habituellement une fonction en calculant sa valeur en un point. Toutefois cette méthode fait jouer un rôle considérable aux irrégularités (discontinuités par exemple) de la fonction. L'idée sous-jacente à la théorie des distributions est qu'il existe un meilleur procédé d'évaluation : calculer une moyenne des valeurs de la fonction dans un domaine de plus en plus resserré autour du point d'étude. En envisageant des moyennes pondérées, on est donc conduit à examiner des expressions de la forme

$I_f(\varphi)=\int_\R f(x)\varphi(x)\,\mathrm dx$

dans laquelle la fonction à évaluer 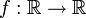$f:\mathbb{R}\rightarrow\mathbb{R}$ est une fonction localement intégrable et 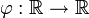$\varphi:\mathbb{R}\rightarrow\mathbb{R}$ est une fonction appelée « fonction test », indéfiniment dérivable et identiquement nulle en dehors d'un ensemble borné.

L'intégrale 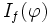$I_f(\varphi)$ est un nombre réel qui dépend de façon linéaire et continue de $\varphi$ . On voit donc que l'on peut associer à une fonction intégrable $f$ une forme linéaire continue sur l'espace des fonctions test. Deux fonctions localement intégrables $f$ et $g$ qui donnent la même forme linéaire continue sont égales presque partout. Ce qui signifie qu'il revient au même de connaître $f$ ou la forme linéaire d'évaluation des fonctions test associée.

D'une manière plus générale, si $μ$ est une mesure sur les réels et $\varphi$ est une fonction test, alors l'intégrale

$I_\mu(\varphi)=\int_\R \varphi(x)\,\mathrm d\mu(x)$

est un nombre réel qui dépend de façon linéaire et continue de $\varphi$ . Les mesures peuvent aussi être associées à des formes linéaires continues sur l'espace des fonctions test. Cette notion de « forme linéaire continue sur l'espace des fonctions test » est par conséquent utilisée comme définition des distributions.

Les distributions peuvent être multipliées par un nombre réel quelconque et additionnées entre elles. L'ensemble des distributions forme ainsi un espace vectoriel réel. Il n'est pas possible de définir en général le produit de deux distributions en tant que généralisation du produit ponctuel de deux fonctions, mais les distributions peuvent être multipliées par des fonctions indéfiniment dérivables.

Théorie des distributions

Espace des fonctions tests

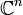Soit $Ω$ un sous-espace topologique de $\mathbb{R}^n$ (ou $\mathbb{C}^n$ ). L'espace des fonctions tests 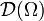$\mathcal{D}(\Omega)$ est l'ensemble des fonctions à valeurs réelles indéfiniment dérivables de $Ω$ à support compact inclus dans $Ω$ . On munit cet espace vectoriel de la topologie suivante : un ensemble 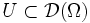$U \subset \mathcal{D}(\Omega)$ est ouvert ssi pour tout 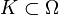$K \subset \Omega$ compact et 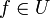$f \in U$ dont le support est inclus dans $K$ , il existe $ε > 0$ et 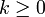$k \ge 0$ tels que

$\{ g \in \mathcal{D}(\Omega)\;\mid\; \operatorname{supp}(g) \subset K\quad\text{et}\quad\forall x \in K,\; |f^{(k)}(x)-g^{(k)}(x)|\le \epsilon \}\;\subset\;U.$

Muni de cette topologie, 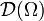$\mathcal{D}(\Omega)$ est un espace vectoriel topologique non métrisable.

Exemple de fonction test sur $\mathbb{R}$ :

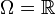Pour $\Omega=\mathbb{R}$ on définit

$\varphi : x\longmapsto \begin{cases} \exp\left(-\frac{1}{1-x^2}\right) & \text{si }|x|<1\\ 0 & \text{sinon} \end{cases}$

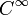La fonction $\varphi$ est $C^\infty$ sur $\mathbb{R}$ et son support est l'intervalle $[ - 1,1]$ .

Exemple de fonction test $\mathbb{R}^n$ :

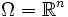Pour $\Omega=\mathbb{R}^n$ on définit

$\varphi : x\longmapsto \begin{cases} \exp\left(-\frac{1}{1-||x||^2}\right) & \text{si }||x||<1\\ 0 & \text{sinon} \end{cases}$

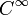La fonction $\varphi$ est $C^\infty$ sur $\mathbb{R}^n$ et son support est la boule fermée B(0,1).

Distributions

Définition

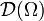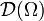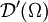Une distribution est une forme linéaire continue sur $\mathcal{D}(\Omega)$ . L'ensemble des distributions est donc le dual topologique de $\mathcal{D}(\Omega)$ on le note donc $\mathcal{D}'(\Omega)$ .

Notation

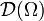Si $T$ est une distribution et $\varphi$ une fonction test de $\mathcal{D}(\Omega)$ alors on note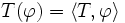 $T(\varphi)=\langle T,\varphi \rangle$

Exemples

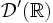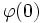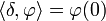Dans $\mathcal{D}'(\mathbb{R})$ , l'application qui à $\varphi$ associe $\varphi(0)$ est une distribution. C'est la distribution de Dirac, introduite par Paul Dirac et notée $δ$ . On a par définition $\langle\delta,\varphi\rangle=\varphi(0)$ .

Une fonction localement intégrable $f$ représente aussi une distribution $T f$ définie par la forme intégrale suivante :

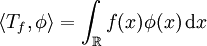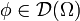$\langle T_f,\phi\rangle=\int_{\mathbb{R}}f(x)\phi(x)\,\mathrm dx$ pour toute fonction $\phi\in\mathcal{D}(\Omega)$ .

Ainsi pour des fonctions localement intégrables on pourra confondre une fonction et sa distribution associée. Les distributions ainsi définies sont appelées distributions régulières.

Un autre exemple célèbre est la fonction de Heaviside que l'on note $Y$ ou $H$ , définie par:

$\langle Y,\phi \rangle=\int_0^{+\infty}\phi(x)\,\mathrm dx$

Dérivation des distributions

Pour définir la dérivée d'une distribution, voyons d'abord le cas d'une fonction différentiable et intégrable 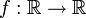$f:\mathbb{R}\rightarrow\mathbb{R}$ . Si $\varphi$ est une fonction test, alors faisant une intégration par parties on peut écrire

$\int_\R f'(x) \varphi(x)\,\mathrm dx = -\int_\R f(x)\varphi'(x)\,\mathrm dx \qquad\mathrm{soit}\qquad I_{f'}(\varphi)=I_{-f}(\varphi')$

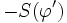Comme la fonction $\varphi$ est nulle en dehors d'un ensemble borné, les problèmes de bords peuvent être ignorés. Si $S$ est une distribution, cet exemple suggère que l'on puisse définir sa dérivée $S'$ comme la forme linéaire qui à une fonction test $\varphi$ fait correspondre la valeur $-S(\varphi')$ . On pose donc :

$\langle S', \varphi \rangle = - \langle S, \varphi' \rangle$

Cette définition étend la notion ordinaire de dérivée : chaque distribution devient indéfiniment dérivable et l'on peut démontrer les propriétés usuelles des dérivées.

Par exemple la dérivée au sens des distributions de la fonction caractéristique de 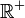$\R^+$ (ou fonction de Heaviside) est la distribution de Dirac en 0.

Bibliographie

Laurent Schwartz, Méthodes mathématiques pour les sciences physiques, Hermann, (1965)

Documents en ligne

(fr)Analyse réelle et distributions : cours de Master 1 (pdf) par un universitaire.
(en)Cours d'introduction aux distributions (Master 1) (pdf) par un universitaire.

Portail des mathématiques

Ce document provient de « Distribution (math%C3%A9matiques)#Th.C3.A9orie des distributions ».

Catégorie : Théorie des distributions

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonctions tests de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Espace des fonctions tests — Distribution (mathématiques) Pour les articles homonymes, voir Distribution. En analyse mathématique, une distribution (également appelée fonction généralisée) est un objet qui généralise la notion de fonction et de mesure. La théorie des… … Wikipédia en Français
Fonctions test — Fonction support Soit un ouvert de , et soit . On appelle support de f, noté Supp(f), l ensemble défini par: L ensemble des fonctions tests induit, noté , est l ensemble des fonctions … Wikipédia en Français
AÉRODYNAMIQUE — L’aérodynamique, dont l’étymologie évoque immédiatement l’action de l’air en mouvement, est la science qui étudie les différents aspects de cette action, notamment les forces, pressions et moments qui résultent du déplacement des corps dans… … Encyclopédie Universelle
Distribution (Mathématiques) — Pour les articles homonymes, voir Distribution. En analyse mathématique, une distribution (également appelée fonction généralisée) est un objet qui généralise la notion de fonction et de mesure. La théorie des distributions étend la notion de… … Wikipédia en Français
Distribution (analyse mathematique) — Distribution (mathématiques) Pour les articles homonymes, voir Distribution. En analyse mathématique, une distribution (également appelée fonction généralisée) est un objet qui généralise la notion de fonction et de mesure. La théorie des… … Wikipédia en Français
Distribution (analyse mathématique) — Distribution (mathématiques) Pour les articles homonymes, voir Distribution. En analyse mathématique, une distribution (également appelée fonction généralisée) est un objet qui généralise la notion de fonction et de mesure. La théorie des… … Wikipédia en Français
Distribution (mathematiques) — Distribution (mathématiques) Pour les articles homonymes, voir Distribution. En analyse mathématique, une distribution (également appelée fonction généralisée) est un objet qui généralise la notion de fonction et de mesure. La théorie des… … Wikipédia en Français
Distribution (mathématiques) — Pour les articles homonymes, voir Distribution. En analyse mathématique, une distribution (également appelée fonction généralisée) est un objet qui généralise la notion de fonction et de mesure. La théorie des distributions étend la notion de… … Wikipédia en Français
Distributions en mathématiques — Distribution (mathématiques) Pour les articles homonymes, voir Distribution. En analyse mathématique, une distribution (également appelée fonction généralisée) est un objet qui généralise la notion de fonction et de mesure. La théorie des… … Wikipédia en Français
Fonction test — Distribution (mathématiques) Pour les articles homonymes, voir Distribution. En analyse mathématique, une distribution (également appelée fonction généralisée) est un objet qui généralise la notion de fonction et de mesure. La théorie des… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonctions tests

Distribution (mathématiques)

Sommaire

Idées de bases