Fonction hyperbolique

En mathématiques, on appelle fonctions hyperboliques les fonctions cosinus hyperbolique, sinus hyperbolique et tangente hyperbolique. Les noms de sinus, cosinus et tangente proviennent de leur ressemblance avec les fonctions trigonométriques (ou circulaires) et le terme de hyperbolique provient de leur relation avec l'hyperbole d'équation $x 2 - y 2 = 1$ .

Elles sont utilisées en analyse pour le calcul intégral, la résolution des équations différentielles mais aussi en géométrie hyperbolique.

Histoire

Les fonctions hyperboliques ont été inventées par le jésuite Vincenzo Riccati dans les années 1760 alors qu'il cherchait, avec son collègue Saladini, à calculer l'aire sous l'hyperbole d'équation $x 2 - y 2 = 1$ . La méthode géométrique qu'il employa alors était très similaire à celle que l'on peut utiliser pour calculer l'aire d'un cercle d'équation $x 2 + y 2 = 1$ . Le calcul de l'aire du cercle fait intervenir les fonctions trigonométriques classiques que Riccati nommait cosinus et sinus circulaires. Par analogie, il appela alors les fonctions qu'il venait de créer cosinus et sinus hyperboliques. Ce fut un choix heureux, car cette ressemblance ne s'arrête pas à la méthode de calcul d'aire mais aussi à toutes les formules trigonométriques. Cependant, pourtant au fait du travail de son contemporain Euler, il n'utilisa pas la fonction exponentielle pour les définir mais seulement des considérations géométriques. L'autre grand mathématicien ayant étudié les fonctions hyperboliques est Johann Heinrich Lambert qui en fit une étude complète en 1770. Cette quasi simultanéité fait que l'on attribue parfois à Lambert la paternité des fonctions hyperboliques bien que les écrits de Riccati lui soient antérieurs de quelques années.

Définitions

Les fonctions hyperboliques sont analogues aux fonctions trigonométriques ou fonctions circulaires. Ce sont les fonctions :

Sinus hyperbolique

Cosinus hyperbolique

Tangente hyperbolique

Sinus hyperbolique

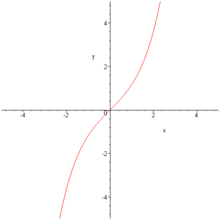
Article détaillé : Sinus hyperbolique.

Définie comme étant la partie impaire de la fonction exponentielle, c’est-à-dire par :

$\operatorname{sh}(x) = \frac{e^{x} - e^{-x}}{2}$

sinh – ou sh – est une bijection de classe $C^\infty$ de $\R$ dans $\R$ strictement croissante, et impaire. Sa dérivée est le cosinus hyperbolique. Son application réciproque s'appelle argument sinus hyperbolique et est notée argsh ou argsinh.

Cosinus hyperbolique

Article détaillé : Cosinus hyperbolique.

Définie comme étant la partie paire de la fonction exponentielle, c’est-à-dire par :

$\operatorname{ch}(x) = \frac{e^{x} + e^{-x}}{2}$

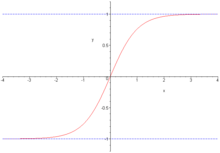
cosh – ou ch – est une application de $\R$ dans $[1;+\infty[$ strictement croissante sur $\R^+$ , et paire. cosh est de classe $C^{\infty}$ sur $\R$ et sa dérivée est le sinus hyperbolique. Sa restriction à $\R^+$ est une bijection à valeurs dans $[1;+\infty[$ dont l'application réciproque, argument cosinus hyperbolique, est notée argch ou argcosh.

Tangente hyperbolique

Article détaillé : Tangente hyperbolique.

Définie par :

$\operatorname{th}(x) = \frac{\operatorname{sh}(x)}{\operatorname{ch}(x)} = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$

th – ou tanh – est une bijection de classe $C^\infty$ de $\R$ dans $] - 1;1[$ strictement croissante, et impaire. Sa dérivée est $\tfrac{1}{\operatorname{ch}^2} = 1-\operatorname{th}^2$ . Son application réciproque s'appelle argument tangente hyperbolique et est notée argth ou argtanh.

Cotangente hyperbolique

Définie par :

$\coth(x) = \frac{\operatorname{ch}(x)}{\operatorname{sh}(x)} = \frac{e^{x} + e^{-x}}{e^{x} - e^{-x}}$

coth est une bijection de classe $C^\infty$ de $\R^*$ dans $]-\infty;-1[ \cup ]1;+\infty[$ . Sa dérivée est $\tfrac{-1}{\operatorname{sh}^2}=1-\coth^2$ . Son application réciproque, argument cotangente hyperbolique, est notée argcoth.

Sécante hyperbolique

Définie par :

$\forall x \in \R,\quad\operatorname{sech}(x) = \frac{1}{\operatorname{ch}(x)}$

Cosécante hyperbolique

Définie par :

$\forall x \in \R^*,\quad\operatorname{cosech}(x) = \frac{1}{\operatorname{sh}(x)}$

Tableau de variations

Les fonctions sh, th, et coth sont impaires et la fonction ch est paire, on peut donc réduire leur domaine d'étude à [0,+ $\infty$ [.

x	0		+ $\infty$
ch x	1	$\nearrow$	+ $\infty$
sh x	0	$\nearrow$	+ $\infty$
th x	0	$\nearrow$	+1
coth x	+ $\infty$	$\searrow$	+1

Propriétés

Par construction,

$\qquad e^{+x} = \operatorname{ch}(x) + \operatorname{sh}(x)$

$\qquad e^{-x} = \operatorname{ch}(x) - \operatorname{sh}(x)$

Ainsi, la formule suivante est vraie pour tout réel x :

$\operatorname{ch}^2x - \operatorname{sh}^2x \,=\, 1$

De même que les points (cos x, sin x) décrivent un cercle lorsque x parcourt $\R$ , les points (ch x, sh x) décrivent une branche d'hyperbole ;

Le paramètre x ne peut pas être interprété comme un angle, ni comme une longueur d'arc ; les fonctions hyperboliques ne sont pas des fonctions périodiques.

La fonction ch admet 1 pour minimum, pour x = 0.

La fonction sh est impaire et ainsi sh(0) = 0.

Les fonctions hyperboliques satisfont à des relations, très ressemblantes aux identités trigonométriques. En fait, la règle d'Osborn^[1] dit que l'on peut convertir n'importe quelle identité trigonométrique en une identité hyperbolique en la développant complètement à l'aide de puissances entières de sinus et cosinus, changeant sin en sh et cos en ch, et remplaçant le signe de chaque terme qui contient un produit de deux sinus en son opposé.

Cela nous permet d'obtenir par exemple, les formules d'addition et de soustraction :

$\operatorname{sh}(x + y) \,=\, \operatorname{sh}(x)\, \operatorname{ch}(y) + \operatorname{ch}(x)\, \operatorname{sh}(y)$

$\operatorname{ch}(x + y) \,=\, \operatorname{ch}(x)\, \operatorname{ch}(y) + \operatorname{sh}(x)\, \operatorname{sh}(y)$

$\operatorname{sh}(x - y) \,=\, \operatorname{sh}(x)\, \operatorname{ch}(y) - \operatorname{ch}(x)\, \operatorname{sh}(y)$

$\operatorname{ch}(x - y) \,=\, \operatorname{ch}(x)\, \operatorname{ch}(y) - \operatorname{sh}(x)\, \operatorname{sh}(y)$

et des « formules d'angle moitié » (la deuxième étant valide si x est positif ou nul) :

$\operatorname{ch}\left(\frac{x}{2}\right) \,=\, \sqrt{\frac{\operatorname{ch}(x) + 1}{2}}$

$\operatorname{sh}\left(\frac{x}{2}\right) \,=\, \sqrt{\frac{\operatorname{ch}(x)-1}{2}}$

De ces expressions on déduit les formules suivantes relatives à la tangente hyperbolique :

$1 - \operatorname{th}^2(x)\,=\, \frac{1}{\operatorname{ch}^2(x)}$

$\operatorname{th}(x+y)\,=\,\frac{\operatorname{th}(x)+\operatorname{th}(y)}{1+\operatorname{th}(x)\,\operatorname{th}(y)}$

$\operatorname{th}\left(\frac{x}{2}\right) \,=\, \sqrt{\frac{\operatorname{ch}(x) - 1}{\operatorname{ch}(x)+1}}$

On a de même:

$\operatorname{sh}(2 x) \,=\, 2\, \operatorname{ch}(x)\,\operatorname{sh}(x)$

$\operatorname{ch}(2 x) \,=\, \operatorname{ch}^2(x) + \operatorname{sh}^2(x) \,=\, 1 + 2\,\operatorname{sh}^2(x) \,=\, 2\, \operatorname{ch}^2(x) - 1$

$\operatorname{th}(2 x) \,=\, \frac{2\, \operatorname{th}(x)}{\operatorname{th}^2(x) + 1}$

La fonction cosinus hyperbolique est convexe. Elle intervient dans la définition de la chaînette, laquelle correspond à la forme que prend un câble suspendu à ses extrémités et soumis à son propre poids.

Puisque la fonction exponentielle peut être prolongée à l'ensemble des nombres complexes, nous pouvons aussi étendre les définitions des fonctions hyperboliques à l'ensemble des nombres complexes. Les fonctions sinus hyperbolique et cosinus hyperbolique sont alors holomorphes et même entières.

Des formules d'Euler, on obtient immédiatement:

$\cos(x) = \operatorname{ch}(\mathrm i x)$

$\mathrm i\sin(x) = \,\operatorname{sh}(\mathrm i x)$

Ou encore:

$\operatorname{ch}(x) = \cos(\mathrm i x)$

$\operatorname{sh}(x) = -\mathrm i\,\sin(\mathrm i x)$

Applications réciproques

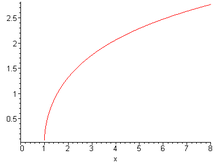
Argument sinus hyperbolique

argsh – ou argsinh – est l'application réciproque de sh^[2]. C'est une bijection de $\R$ dans $\R$ , impaire et strictement croissante. argsh est dérivable sur $\R$ et sa dérivée est $x \mapsto \tfrac{1}{\sqrt{x^2+1}}$ . argsh admet une forme logarithmique, c’est-à-dire qu'il peut se mettre sous la forme d'un logarithme :

$\arg\operatorname{sh}(x) = \ln\left(x + \sqrt{x^2 +1 }\right)$

Argument cosinus hyperbolique

argch^[3] est l'application réciproque de la restriction de ch dans $\R^+$ . C'est une bijection de $[1,+\infty[$ dans $\R^+$ , strictement croissante. argch est dérivable sur $]1,+\infty[$ et sa dérivée est $x \mapsto \frac{1}{\sqrt{x^2-1}}$ . argch admet une forme logarithmique:

$\arg \operatorname{ch}(x) = \ln\left(x + \sqrt{x^2 -1}\right)$

Argument tangente hyperbolique

argth – ou argtanh – est l'application réciproque de th^[4]. C'est une bijection de $] - 1;1[$ dans $\R$ , impaire, strictement croissante. argth est dérivable sur $] - 1;1[$ et sa dérivée est $x \mapsto \tfrac{1}{1-x^2}$ . argth admet une forme logarithmique :

$\arg \operatorname{th}(x) = \frac{1}{2}\ln\left(\frac{1+x}{1-x}\right)$

Argument cotangente hyperbolique

argcoth est l'application réciproque de coth^[5]. C'est une bijection de $]-\infty;-1[ \cup ]1;+\infty[$ dans $\R^*$ . argcoth est dérivable sur $]-\infty;-1[ \cup ]1;+\infty[$ et sa dérivée est $x \mapsto \tfrac{1}{1-x^2}$ . argcoth admet une forme logarithmique :

$\arg\coth(x) = \frac{1}{2}\ln\left(\frac{x+1}{x-1}\right)$

Démonstrations de ces résultats

Le calcul explicite de ces formes logarithmiques revient à résoudre, par exemple, l'équation $\operatorname{sh} (t)= x$ ; posant $e t = T$ , on est amené à l'équation du second degré $T 2 - 2 x T - 1 = 0$ , dont la seule solution positive est $T=x+\sqrt {1+x^2}$ , mais il peut être plus simple de remarquer que, puisque $\operatorname{ch}^2t-\operatorname{sh}^2t=1$ , on aura $e^t=\operatorname{sh} t+\operatorname{ch} t= x+\sqrt {1+x^2}$ .

Notes

↑ (en) Eric W. Weisstein, « Osborn's Rule », MathWorld
↑ La norme ISO 31-11 recommande la notation arsinh pour cette fonction
↑ La norme ISO 31-11 recommande la notation arcosh pour cette fonction
↑ La norme ISO 31-11 recommande la notation artanh pour cette fonction
↑ La norme ISO 31-11 recommande la notation arcoth pour cette fonction

Voir aussi

Liens internes

Liens externes

GonioLab: visualisation du cercle trigonométrique, des fonctions trigonométriques et des fonctions hyperboliques (Java Web Start)
(en) Riccati pour la définition géométrique des fonctions hyperboliques

Portail de l'analyse

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction hyperbolique de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Fonction Hyperbolique — En mathématiques, on appelle fonctions hyperboliques les fonctions cosinus hyperbolique, sinus hyperbolique et tangente hyperbolique. Les noms de sinus, cosinus et tangente proviennent de leur ressemblance avec les fonctions trigonométriques (ou… … Wikipédia en Français
fonction hyperbolique — hiperbolinė funkcija statusas T sritis fizika atitikmenys: angl. hyperbolic function vok. hyperbolische Funktion, f rus. гиперболическая функция, f pranc. fonction hyperbolique, f … Fizikos terminų žodynas
Hyperbolique — Fonction hyperbolique En mathématiques, on appelle fonctions hyperboliques les fonctions cosinus hyperbolique, sinus hyperbolique et tangente hyperbolique. Les noms de sinus, cosinus et tangente proviennent de leur ressemblance avec les fonctions … Wikipédia en Français
hyperbolique — [ ipɛrbɔlik ] adj. • 1541; lat. hyperbolicus, gr. huperbolikos I ♦ Rhét. Caractérisé par l hyperbole. Style hyperbolique. Cour. Des compliments hyperboliques. ⇒ emphatique, grandiloquent. Philos. Le doute hyperbolique (Descartes). II ♦ (1646) 1 ♦ … Encyclopédie Universelle
Fonction De Gudermann — En mathématiques, la fonction de Gudermann, appelée aussi parfois gudermannien, et notée gd, nommée en l honneur de Christoph Gudermann (1798 1852), fait le lien entre la trigonométrie circulaire et la trigonométrie hyperbolique sans faire… … Wikipédia en Français
Fonction de gudermann — En mathématiques, la fonction de Gudermann, appelée aussi parfois gudermannien, et notée gd, nommée en l honneur de Christoph Gudermann (1798 1852), fait le lien entre la trigonométrie circulaire et la trigonométrie hyperbolique sans faire… … Wikipédia en Français
Fonction sinus hyperbolique — ● Fonction sinus hyperbolique fonction définie sur R : x ↦ sh x. (Sa dérivée est la fonction cosinus hyperbolique.) … Encyclopédie Universelle
Fonction tangente hyperbolique — ● Fonction tangente hyperbolique fonction , définie sur R et notée th. (Elle a pour fonction dérivée x ↣ 1 − th2 x.) … Encyclopédie Universelle
Fonction cosinus hyperbolique — ● Fonction cosinus hyperbolique fonction définie sur R : x ↦ ch x … Encyclopédie Universelle
Fonction cotangente hyperbolique — ● Fonction cotangente hyperbolique fonction x ↦ ch x / sh x définie sur R. (On la note coth.) … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Fonction hyperbolique

Sommaire

Histoire