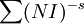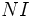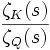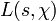Fonction Zeta de Dedekind

Fonction Zeta de Dedekind

Fonction zêta de Dedekind

En mathématiques, la fonction zêta de Dedekind est une série de Dirichlet définie pour tout corps de nombres \mathbb{K}, et notée

\zeta_K(s)\,

où s est une variable complexe. C'est la somme infinie

\sum (NI)^{-s}\,

prise sur tous les idéaux I de l'anneau des entiers 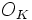O_K\, de K, avec 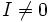I \ne {0}\, , où

NI\,

exprime la norme de I (dans le corps rationnel Q). Ceci est égal à la cardinalité de

O_K/I\, ,

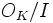en d'autres mots, le nombre de classes de résidus modulo I. Dans le cas 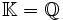\mathbb{K} = \mathbb{Q} cette définition se réduit à la fonction zêta de Riemann.

Les propriétés de 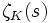\zeta_K(s)\, comme une fonction méromorphe ont une signification considérable dans la théorie algébrique des nombres. Elle possède un produit eulérien, avec un facteur pour un nombre premier donné p, le produit pris sur tous les idéaux premiers P de OK divisant p de

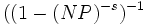((1 - (NP)^{-s})^{-1}\, .

Ceci est l'expression en termes analytiques de l'unicité de la factorisation en nombres premiers des idéaux I.

Il est connu (démontré en général en premier par Erich Hecke) que ζK(s) a un prolongement analytique dans le plan complexe entier en fonction méromorphe, ayant un pôle simple seulement à s = 1. Le résidu à ce pôle est une quantité importante, impliquant les invariants du groupe des unités et du groupe de classe de K. Il existe une équation fonctionnelle pour la fonction zêta de Dedekind, en reliant ses valeurs à s et 1 − s.

Pour le cas dans lequel K est une extension abélienne de Q, sa fonction zêta de Dedekind peut être écrite comme un produit de fonctions L de Dirichlet. Par exemple, quand K est un corps quadratique ceci montre que le rapport

\frac{\zeta_K(s)}{\zeta_Q(s)}\,

est une fonction L

L(s,\chi)\,

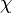où \chi\, est un symbole de Jacobi comme caractère de Dirichlet. Ceci est une formulation de la loi de réciprocité quadratique.

En général si K est une extension galoisienne de Q avec un groupe de Galois G, sa fonction zêta de Dedekind possède une factorisation comparable en termes de fonctions L d'Artin. Celles-ci sont attachées aux représentations linéaires de G.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Fonction z%C3%AAta de Dedekind ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction Zeta de Dedekind de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Fonction Zeta De Dedekind — Fonction zêta de Dedekind En mathématiques, la fonction zêta de Dedekind est une série de Dirichlet définie pour tout corps de nombres , et notée où s est une variable complexe. C est la somme infinie prise sur tous les idéaux I de l anneau des… …   Wikipédia en Français

  • Fonction zeta de Dedekind — Fonction zêta de Dedekind En mathématiques, la fonction zêta de Dedekind est une série de Dirichlet définie pour tout corps de nombres , et notée où s est une variable complexe. C est la somme infinie prise sur tous les idéaux I de l anneau des… …   Wikipédia en Français

  • Fonction zeta de dedekind — Fonction zêta de Dedekind En mathématiques, la fonction zêta de Dedekind est une série de Dirichlet définie pour tout corps de nombres , et notée où s est une variable complexe. C est la somme infinie prise sur tous les idéaux I de l anneau des… …   Wikipédia en Français

  • Fonction zêta de Dedekind — En mathématiques, la fonction zêta de Dedekind est une série de Dirichlet définie pour tout corps de nombres , et notée où s est une variable complexe. C est la somme infinie prise sur tous les idéaux I de l anneau des entiers de K, avec …   Wikipédia en Français

  • Fonction Zeta — Fonction zêta Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction… …   Wikipédia en Français

  • Fonction zeta — Fonction zêta Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction… …   Wikipédia en Français

  • Fonction zêta — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction zêta de… …   Wikipédia en Français

  • Fonction dzêta — Fonction zêta Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. La fonction zêta (d après la lettre grecque zêta, ou ζ) est le nom de nombreuses fonctions en mathématiques. La plus connue est la fonction… …   Wikipédia en Français

  • ZÊTA (FONCTION) — Issues d’un calcul formel d’Euler, la «fonction zêta» de Riemann et les «fonctions L» de Dirichlet ont été jusqu’ici les outils analytiques les plus puissants pour étudier la répartition et les propriétés des nombres premiers (cf. théorie des… …   Encyclopédie Universelle

  • Fonction Theta — Fonction thêta En mathématiques, on appelle fonctions thêta certaines fonctions spéciales d une ou de plusieurs variables complexes. Elles apparaissent dans plusieurs domaines, comme l étude des variétés abéliennes, des espace de modules, et les… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”