- Fonction W de Lambert
-
En mathématiques, et plus précisément en analyse, la fonction W de Lambert, nommée ainsi d'après Johann Heinrich Lambert, et parfois aussi appelée la fonction Oméga, est la réciproque de la fonction f définie par f(w) = wew, c'est-à-dire que pour tout nombre complexe z, nous avons W(z)eW(z) = z. Puisque la fonction f n'est pas injective, la fonction W est multiforme.
Sommaire
Historique
Lambert s'est intéressé à l'équation connue sous le nom d'équation transcendante de Lambert en 1758[1], ce qui conduisit à une note de Leonhard Euler en 1783[2] qui discutait le cas particulier de wew. La première description de la fonction W semble due à George Pólya et Gábor Szegő (en) en 1925[3]. La fonction de Lambert fut "redécouverte" tous les dix ans environ dans des applications spécialisées, mais son importance ne fut pas vraiment appréciée avant les années 1990. Lorsqu'il fut annoncé que la fonction de Lambert donnait une solution exacte aux valeurs propres de l'énergie du système quantique correspondant au modèle décrit par l'opérateur de Dirac à puits double pour le cas de charges égales - un problème physique fondamental - Corless et d'autres développeurs du système Maple firent une recherche bibliographique et découvrirent que cette fonction apparait un peu partout dans des applications pratiques[4].
Propriétés élémentaires
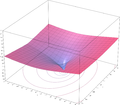
 Représentation graphique de la branche W0 de la fonction W de Lambert
Représentation graphique de la branche W0 de la fonction W de LambertSi nous nous limitons aux arguments réels x ≥ −1⁄e, il existe une fonction et une seule W0 à valeurs réelles
 telle que x = f(W0(x)) = W0(x)exp(W0(x)) ; c'est la branche principale de W dans ce domaine. La représentation graphique de W0 figure à droite (on note généralement W-1 l'autre branche à valeurs réelles, c'est-à-dire la branche correspondant aux arguments x tels que
telle que x = f(W0(x)) = W0(x)exp(W0(x)) ; c'est la branche principale de W dans ce domaine. La représentation graphique de W0 figure à droite (on note généralement W-1 l'autre branche à valeurs réelles, c'est-à-dire la branche correspondant aux arguments x tels que  , et à valeurs
, et à valeurs  ).
).Voici quelques valeurs remarquables de W, obtenues simplement en remarquant que f(0)=0, f(1)=e, f(-1)=-1/e, etc. :
 où Ω est la constante oméga
où Ω est la constante oméga
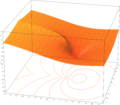
On peut bien sûr obtenir de même des valeurs complexes de W (x) pour certains x< −1⁄e; ainsi
La fonction W de Lambert ne peut pas être exprimée à l'aide de fonctions élémentaires.
La formule de dérivation des bijections réciproques montre que sa dérivée est:
ce qui a pour conséquence que W satisfait l'équation différentielle :
 pour x ≠ −1⁄e ; cette équation est d'ailleurs à variables séparables, et ses autres solutions sont toutes de la forme
pour x ≠ −1⁄e ; cette équation est d'ailleurs à variables séparables, et ses autres solutions sont toutes de la forme  .
.
La fonction W, et beaucoup de fonctions impliquant W, peuvent être intégrées en utilisant le changement de variable w = W(x), i.e. x = wew :
Méthodes de calcul
Par la série de Taylor
La série de Taylor de W0 au voisinage de 0 peut être obtenue par l'utilisation du théorème d'inversion de Lagrange et est donnée par
Le rayon de convergence est égal à 1⁄e. Cette série peut être prolongée en une fonction holomorphe définie en tout nombre complexe n'appartenant pas à l'intervalle réel ]−∞, –1⁄e] ; cette fonction holomorphe est aussi appelée la branche principale de la fonction W de Lambert.
Comme limite d'une suite
On peut calculer W0(x) de manière itérative, en commençant avec une valeur initiale w0 égale à 1 et en calculant les termes de la suite
 .
.
Si cette suite converge, on voit aisément que sa limite est W0(x). On démontre que c'est en effet le cas si
![x \in [-e^{-1};e]](a/94a1e3813fd6d6614d1599494cd04626.png) :
:Il est moins simple, mais beaucoup plus efficace, d'utiliser la méthode de Newton, partant de w0 = 1, et posant
cette suite converge (très rapidement) vers W0(x) pour tout x > 1 / e.
Approximation asymptotique
On a pour x tendant vers
 le développement asymptotique à 3 termes suivant[5] :
le développement asymptotique à 3 termes suivant[5] : .
.
Utilisation
Beaucoup d'équations impliquant des exponentielles peuvent être résolues par l'utilisation de la fonction W. La stratégie générale est de déplacer toutes les instances de l'inconnue d'un côté de l'équation et de le faire ressembler à xex. À ce point la fonction W nous fournit la solution.
Exemples
- Exemple 1
Par exemple, pour résoudre l'équation 2t = 5t, nous divisons par
 pour obtenir −ln(2)⁄5 = −ln(2)t exp(−ln(2)t). L'application de la fonction W donne alors −ln(2)t = W(−ln(2)⁄5), soit t = −W(ln(2)/5)⁄ln(2).
pour obtenir −ln(2)⁄5 = −ln(2)t exp(−ln(2)t). L'application de la fonction W donne alors −ln(2)t = W(−ln(2)⁄5), soit t = −W(ln(2)/5)⁄ln(2).- Exemple 2
Avec la fonction W de Lambert, on peut résoudre des équations du type xx = z par:
De même, la bijection réciproque de
 peut être obtenue explicitement : résolvant l'équation g(x) = x + ex = y, on remarque d'abord qu'elle équivaut, en posant X = ex à XeX = ey, et donc x = g − 1(y) = ln W(ey).
peut être obtenue explicitement : résolvant l'équation g(x) = x + ex = y, on remarque d'abord qu'elle équivaut, en posant X = ex à XeX = ey, et donc x = g − 1(y) = ln W(ey).- Exemple 3
Quand une tétration complexe infinie converge:
la fonction W de Lambert fournit la valeur de la limite réelle comme:
où log(z) représente la branche principale de la fonction logarithme complexe.
- Exemple 4
La solution de l'équation:
est donnée avec la fonction W de lambert.
- Exemple 5
La solution pour connaître la valeur du courant dans un circuit en série de diode/résistance peut être donnée par la fonction W de Lambert. Voir la modélisation d'une diode (en).
Diverses formules
On obtient alors par changements de variable les égalités remarquables :
Représentations
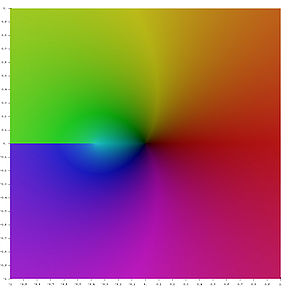
- Représentation de la partie réelle, de la partie imaginaire et du module de la fonction W de Lambert dans le plan complexe
Généralisations
La fonction W de Lambert fournit des solutions exactes aux équations "algébriques-transcendantes" (en x) de la forme:
ou a0, c et r sont des constantes réelles. La solution est x = r + W(ce − cr / ao) / c. Les généralisations de la fonction W de Lambert[6] inclut:
- un lien entre la relativité générale et la mécanique quantique (gravité quantique) en dimensions réduites[7] où la partie de droite de l'équation (1) est maintenant un polynôme quadratique en x:
- où r1 et r2 sont des constantes réelles, les racines du polynôme quadratique. Dans ce cas, la solution est une fonction avec un seul argument x mais les termes comme ri et ao sont des paramètres de la fonction. De ce point de vue, la généralisation ressemble à la série hypergéométrique et la fonction de Meijer G mais appartient pourtant à une "classe" différente de fonctions. Quand r1 = r2, chaque côté de (2) peut être factorisé et réduit à (1) et donc la solution se réduit à celle de la fonction standard de W. L'équation (2) est celle gouvernant le champ d'un dilaton - par lequel est dérivée la métrique du système gravitationnel de deux corps dans les dimensions 1+1 (c’est-à-dire une dimension spatiale et une dimension temporelle) pour le cas des masses (au repos) inégales - ainsi que les valeurs propres de l'énergie du système quantique qui consiste du modèle décrit par l'opérateur de Dirac à puits double pour le cas de charges inégales en une dimension.
- les solutions analytiques pour les valeurs propres de l'énergie d'un cas spécial de la version quantique du problème des trois corps, c’est-à-dire l’ion hydrogène moléculaire (en trois dimensions)[8]. La partie de droite de (1) (ou (2)) est maintenant un quotient de "polynômes" d'ordre infini en x:
- où ri et si sont des constantes réelles distinctes et x est une fonction de la valeur propre de l'énergie et la distance internucléaire R. L'équation (3) avec ces cas spécialisés et exprimés dans (1) et (2) correspond à une classe considérable d'équations à délai différentiel.
Les applications de la fonction W de Lambert dans les problèmes de la physique fondamentale ne sont pas épuisées même pour le cas standard exprimé dans (1), comme on vient de le voir dans les domaines de la physique atomique et moléculaire, ainsi qu'en optique[9].
Notes
- Lambert JH, "Observationes variae in mathesin puram", Acta Helveticae physico-mathematico-anatomico-botanico-medica, Band III, 128-168, 1758 (facsimile)
- Euler, L. "De serie Lambertina Plurimisque eius insignibus proprietatibus." Acta Acad. Scient. Petropol. 2, 29-51, 1783. Réimprimée dans Euler, L. Opera Omnia, Series Prima, Vol. 6: Commentationes Algebraicae. Leipzig, Germany: Teubner, pp. 350-369, 1921. (facsimile)
- (en) George Pólya et Gábor Szegő, Aufgaben und Lehrsätze der Analysis, Berlin, Springer-Verlag, 1925
- Corless R.M., Gonnet G.H., Hare D.E.G. et Jeffrey D.J., Lambert's W function in Maple, The Maple Technical Newsletter (MapleTech), 9, pp. 12-22, (1993).
- On trouvera beaucoup plus de termes de ce développement dans l'article de MathWorld consacré à la fonction W (en)
- Scott T.C. et Mann R.B., General Relativity and Quantum Mechanics: Towards a Generalization of the Lambert W Function, AAECC (Applicable Algebra in Engineering, Communication and Computing), vol. 17, no. 1, (avril 2006), pp.41-47, [1]; article Arxiv[2]
- Farrugia P.S., Mann R.B., et Scott T.C., N-body Gravity and the Schrödinger Equation, Class. Quantum Grav. vol. 24, (2007), pp. 4647-4659, [3]; article Arxiv [4]
- Scott T.C., Aubert-Frécon M. et Grotendorst J., New Approach for the Electronic Energies of the Hydrogen Molecular Ion, Chem. Phys. vol. 324, (2006), pp. 323-338, [5]; article Arxiv[6]
- Scott T.C., Lüchow A., Bressanini D. et Morgan III J.D., The Nodal Surfaces of Helium Atom Eigenfunctions, Phys. Rev. A 75, (2007), p. 060101, [7]
Références
- (en) Trott, « Fonction W de Lambert », MathWorld
- (en) Corless et. al. ; « On the Lambert W function » Adv. Computational Maths. 5, 329 - 359 (1996) (ici ou là)
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Lambert W function » (voir la liste des auteurs)
Wikimedia Foundation. 2010.
















 (
(